Journal influence
Bookmark
Next issue
Processing techniques in computer perfomance evaluation of the educational process
The article was published in issue no. № 1, 2012 [ pp. 107 - 111 ]Abstract:In article processing methods in computer coefficient techniques of initial (entrance) and intermediate indicators for reception of target indicators of a rating estimation of educational process (estimated object) with the account of standard logic conditions are considered.
Аннотация:Рассматриваются методы обработки в компьютерных коэффициентных методиках исходных (входных) и проме-жуточных показателей для получения выходных показателей рейтинговой оценки образовательного процесса (оце-ниваемого объекта) с учетом нормативных логических условий оценивания.
| Authors: (dolgov-ai@yandex.ru) - , Ph.D, (dolgov-ai@yandex.ru) - , (dolgov-ai@yandex.ru) - , Ph.D | |
| Keywords: the multiplier., the adder, changeable weight factor, educatioal process, computer coefficient a technique |
|
| Page views: 6932 |
Print version Full issue in PDF (5.33Mb) Download the cover in PDF (1.08Мб) |
В практике оценивания образовательного процесса наиболее востребованы программно реализованные коэффициентные методики благодаря их простоте и приемлемой точности получаемых результатов. Под коэффициентной методикой понимается методика вычисления значения интегрального выходного показателя (или некоторого множества выходных показателей) оцениваемого объекта (процесса) путем суммирования значений вполне определенного множества входных показателей, учитываемых при этом с соответствующими весовыми коэффициентами [1]. Разработка компьютерной коэффициентной методики оценки образовательного процесса (далее – коэффициентной методики), предшествующая ее программной реализации, включает два этапа – математическое описание методов обработки показателей и синтез структурной схемы коэффициентной методики. Математическое описание методов, необходимых для получения рейтинговой оценки образовательного процесса с учетом нормативных логических условий оценивания, включает: - выделение предварительного значения рейтинговой оценки в виде среднего балла, соответствующего комбинациям частных оценок, определяемой логическими условиями оценивания для данного рейтингового интервала; - определение наличия оценок, снижающих значение предварительной рейтинговой оценки; - получение итогового (окончательного) значения рейтинговой оценки путем коррекции ее предварительного значения. Приведем определения основных используемых понятий. Оценка – процесс определения (оценивания) значения показателя, характеризующего результат образовательного процесса. Показатель – качественная и (или) количественная характеристика, вводимая для оценивания отдельного свойства либо совокупности свойств объекта (процесса). В отличие от оценки показатель обычно имеет наименование, обозначение и значение, а при количественной оценке во многих случаях и размерность. Шкала – инструмент для разделения оцениваемых значений рассматриваемых однородных показателей на различимые между собой группы, где отношения между значениями показателей выражены свойствами числового ряда либо ряда наименований [2]. В образовательном процессе в зависимости от вида используемой шкалы различают балльные, качественные (шкала наименований), а иногда и балльно-качественные оценки. Значениями балльной оценки являются целые числа – количество баллов (например, 5, 4, 3, 2). Значения качественной оценки выражаются наименованиями («отлично», «хорошо», «удовлетворительно», «неудовлетворительно»). В последнее время в оценивании образовательного процесса все чаще применяются рейтинговые оценки – числовые оценки, задаваемые с некоторой точностью в (рейтинговых) интервалах численных значений рейтинговой шкалы. Наиболее часто используемая 5-балльная система оценки, а также иногда применяемые системы оценок с несколько большим количеством баллов (например 12-балльная) имеют существенный недостаток – используют ограниченное количество значений (градаций) оценивания, внутри которых объекты оказываются неразличимыми. В связи с этим рассмотрим методы обработки показателей образовательного процесса с использованием как 5-балльных оценок, так и рейтинговых оценок с градацией чисел в рейтинговых интервалах: 4,5≤«отлично»≤5; (1) 3,5≤«хорошо»<4,5; (2) 2,5≤«удовлетворительно»<3,5; (3) 2,0≤«неудовлетворительно»<2,5. В традиционно используемых коэффициентных методиках значения весовых коэффициентов постоянны по величине. Вместе с тем при вычислении значения того или иного показателя могут учитываться вполне определенные логические условия оценивания, учитываемые только с помощью изменяемых весовых коэффициентов [3]. Выделение предварительного значения рейтинговой оценки Рассмотрим данный метод на примере оценивания подготовленности специалиста в рейтинговом интервале «хорошо» при нормативном требовании, задающем логические условия получения итогового значения Rхор рейтинговой оценки «хорошо» лишь в случае следующих комбинаций частных оценок: оценка за практические навыки должна быть не ниже «хорошо», а оценка за теоретические знания не ниже «удовлетворительно». Предварительное значение R′хор рейтинговой оценки Rхор выделяется в виде среднего балла частных оценок практических навыков (ХП) и теоретических знаний (ХТ) лишь в случае выполнения нормативного требования, при этом
Конкретный пример иллюстрируется данными, представленными в таблице.
Первый специалист получил за практику рейтинговую оценку XП=3,4 («удовлетворительно»), а за теорию XТ=5 («отлично»), средняя оценка его подготовленности составила Второй специалист получил оценку за практику XП=4,0 («хорошо»), за теорию XТ=4,4 («хорошо»), и средний балл за его подготовленность такой же: В этой ситуации в соответствии с соотношением 3,5≤«хорошо»<4,5 для среднего балла оба специалиста претендуют на оценку «хорошо». Однако (при несоблюдении условий получения итоговой рейтинговой оценки «отлично») по логическим условиям оценивания итоговая рейтинговая оценка R′хор первого специалиста (ввиду наличия оценки «удовлетворительно» за практику) должна быть исключена из рейтингового интервала «хорошо», что соответствует R′хор=0. Таким образом, надо определить наличие комбинации XП≥3,5 и XТ≥2,5, соответствующей рейтинговой оценке «хорошо», что в коэффициентной методике нереализуемо с использованием одного весового коэффициента, но осуществимо с применением трех изменяемых весовых коэффициентов. Сформируем признак Пр1,2 принадлежности оценки специалиста к рейтинговому интервалу «хорошо» в соответствии с соотношением Пр1,2=XПVП2+XТVТ2, где и Условием наличия комбинации XП≥3,5 и XТ≥2,5, соответствующей рейтинговой оценке «хорошо» (см. табл.), является значение показателя Пр1,2=0, а признаком отсутствия этой комбинации – значение показателя Пр1,2>0 R′хор=X2,1∙V1,R, (4) где X2,1=(XП+XТ)×0,5+Пр1,2;
Таким образом, весовой коэффициент V1,R совместно с признаком принадлежности (Пр1,2) на основании соотношения (4) при наличии комбинации, соответствующей рейтинговой оценке «хорошо» (Пр1,2=0, X2,1>0), обеспечивает формирование значений V1,R=1 и как результат – R′хор= =(XП+XТ)∙0,5, а при отсутствии комбинации (Пр1,2=1, X2,1<0) – значений V1,R=0 и R′хор=0. Фрагмент синтезированной в соответствии с математическим соотношением (4) структурной схемы коэффициентной методики приведен на рисунке 1. Внутри прямоугольников, обозначающих сумматоры входных показателей нижестоящего уровня, указываются обозначения показателей, значения которых равны результату суммирования входных показателей, умноженному на соответствующий весовой коэффициент. В овалах, обозначающих для неизменяемых весовых коэффициентов умножители, а для изменяемых весовых коэффициентов умножители с аддитивной поправкой, для неизменяемых весовых коэффициентов приводятся их значения, а для изменяемых – символические обозначения. Связи между сумматорами и умножителями указаны стрелками. Аналогично строятся и фрагменты структурных схем для других итоговых интегральных рейтинговых оценок подготовленности специалиста. Определение наличия снижающих оценок При определении предварительных рейтинговых оценок могут встречаться комбинации частных оценок, приводящие к одинаковым предварительным значениям рейтинговой оценки, однако комбинации по своему составу могут быть настолько неравноценными, что в соответствие им следует поставить разные рейтинговые значения предварительной оценки.
Коррекцию предварительных рейтинговых оценок можно осуществить следующим образом. Рейтинговый интервал 3,5≤«хорошо»<4,5 разделяется на два диапазона: 4,0≤«хорошо»<4,5 (верхний диапазон), (5) 3,5≤«хорошо»<4,0 (нижний диапазон), (6) при этом полученное значение предварительной рейтинговой оценки R′хор преобразуется так, чтобы в случае возникновения комбинации частных оценок за теорию и практику, не включающей оценку «удовлетворительно», выделить значение R″хор1, принадлежащее верхнему диапазону, а в случае комбинации, включающей такую оценку, выделить значение R″хор2, принадлежащее нижнему диапазону. Выполнение подобного преобразования для оценок, принадлежащих рейтинговому интервалу «хорошо», осуществимо с использованием признака Пр1,3 наличия снижающей оценки (в данном случае «удовлетворительно»): Пр1,3=XП×VП,3+XТ×VТ,3, где
Наличие среди частных оценок XП, XТ хотя бы одной оценки «удовлетворительно» приводит к положительному значению признака наличия снижающей оценки (Пр1,3) за счет умножения хотя бы на один изменяемый весовой коэффициент VП,3 или VТ,3, равный в этом случае единице, либо к нулю при отсутствии снижающих оценок «удовлетворительно» за счет умножения на изменяемые весовые коэффициенты VП,3 и VТ,3, равные в этом случае нулю. С помощью изменяемых весовых коэффициентов V3,1 и V3,2 и признака наличия снижающей оценки (Пр1,3) предварительное значение оценки подготовленности специалиста может быть получено как R″хор1 или R″хор2, причем в зависимости от значений изменяемых весовых коэффициентов V3,1 и V3,2 либо в виде доминирующего отрицательного числа, либо в виде значения R′хор. Математическими соотношениями, описывающими метод определения снижающих оценок, являются следующие: R″хор1=Rхор+Пр1,3V3,1 и R″хор2=Rхор+Пр1,3V3,2, где
Реализация соотношений R″хор1 и R″хор2 представлена на рисунке 2. Аналогично может быть реализован метод определения признака наличия снижающих оценок и в интервале «удовлетворительно». Получение итогового значения рейтинговой оценки
Однако зачастую предварительное значение R″хор1 или R″хор2, хотя и попадает в нужный диапазон соответствующего рейтингового интервала, из-за логического условия оценивания (при разных сочетаниях входных оценок) по абсолютной величине может выйти за границы установленного рейтингового интервала. Для приведения полученного промежуточного значения рейтинговой оценки к установленным границам интервалов (диапазонов) воспользуемся методом линейных преобразований получаемых промежуточных значений рейтинговой оценки. Для интервала «хорошо» максимальные оценки за теорию и практику могут быть равными соответственно «отлично» и «хорошо», а минимальные – «удовлетворительно» и «хорошо». Исходя из устанавливаемых рейтинговых интервалов (1) и (2) получения оценки «хорошо», возможные достигаемые максимальное и минимальное значения среднего балла оценок специалиста соответственно определяются как
Таким образом, реально вычисляемые в виде среднего балла возможные значения итоговой рейтинговой оценки «хорошо» могут оказаться в интервале 3,0≤ «хорошо» ≤ 4,749(9), в то время как установленный рейтинговый интервал (2) «хорошо» должен быть равен 3,5≤ «хорошо» < 4,5.
Коррекция обозначаемых через x полученных предварительных значений рейтинговых оценок R″хор1 и R″хор2 выполнима с помощью линейного преобразования, описываемого функцией (y) одной переменной (x) вида: y=kx+b. (9) Учитывая, что из логических условий оценивания достигаемые максимально возможные значения y и x в случае верхнего диапазона (5) равны соответственно 4,499(9) и 4,749(9), а минимально возможные равны 4,0 и 4,0, составим систему двух линейных уравнений вида
Результаты решения системы уравнений – k1≈0,665342204 и b1≈1,338631184. На основании этого соотношение (9) для верхнего диапазона рейтингового интервала «хорошо» принимает вид у=0,665342204x+1,338631184. (11) Значения k2 и b2 для нижнего диапазона рейтингового интервала «хорошо» определяются аналогично. Убедимся на конкретном примере, что с использованием линейного преобразования (11) реализуется логическое условие получения оценки «хорошо». Пусть частная оценка практических навыков специалиста XП=4,49 («хорошо»), а теории – XТ=5,0 («отлично»). Средний балл его подготовленности R′хор=R″хор1=4,745, что, согласно (1), соответствует рейтинговому интервалу 4,5≤«отлично»≤5. Однако по нормативным условиям получения оценки требуется, чтобы интегральная итоговая оценка Rхор специалиста была не выше оценки за практику, в данном примере равной «хорошо». Подставив полученную промежуточную рейтинговую оценку R″хор1=4,745 в (11), получим Rхор=4,745×0,665342204+1,338631184≈4,496, то есть итоговая рейтинговая оценка специалиста находится в требуемом верхнем диапазоне рейтингового интервала «хорошо», что соответствует заданным нормативным условиям оценивания. Реализация коррекции выполнима с помощью весовых коэффициентов:
Учитывая, что промежуточное значение оценки находится в одном из диапазонов рассматриваемого рейтингового интервала, математическое соотношение, описывающее метод получения итоговой рейтинговой оценки «хорошо» (Rхор), будет иметь вид
Математическое соотношение (12) может быть представлено фрагментом структурной схемы, отображенной на рисунке 3. Аналогично могут быть построены и реализованы соотношения для вычисления рейтинговых оценок R(отл), R(уд) и R(неуд). Литература 1. Долгов А.И., Мартыненко А.Ф., Преснухин В.В. Научные основы построения коэффициентных методик оценки объектов // Системы управления и информационные технологии. 2008. № 4 (34). С. 61–66. 2. Государственная система обеспечения единства измерений. Шкалы измерений. М.: Стандартинформ, 2008. 3. Долгов А.И., Мартыненко А.Ф., Преснухин В.В. Коэффициентная методика с изменяемыми весовыми коэффициентами // Искусственный интеллект. 2008. Т. 4. 2012-1.files/image809.gif | |||||||||||||||||||||||||||||||||||||
| Permanent link: http://swsys.ru/index.php?id=3029&lang=en&page=article |
Print version Full issue in PDF (5.33Mb) Download the cover in PDF (1.08Мб) |
| The article was published in issue no. № 1, 2012 [ pp. 107 - 111 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Основные задачи автоматизации управления образовательным процессом
- Электронные формуляры для компьютерных тренажеров
- Обзор перспективных направлений развития электронного обучения в системах обучения операторов и образовательных космоцентрах
- Управление образовательным процессом
Back to the list of articles

 =4,2 балла.
=4,2 балла. =4,2.
=4,2.


 Так, например, в интервалах оценки «хорошо» при двух результатах оценки подготовленности специалиста – в первом случае оценка за практику 4,4 («хорошо»), за теорию 4,0 («хорошо»), а во втором случае оценка за практику 5,0 («отлично»), а за теорию 3,4 («удовлетворительно») – полученные предварительные рейтинговые оценки, средний балл которых равен 4,2, оказываются одинаковыми и по нормативным условиям оценивания соответствуют рейтинговому интервалу 3,5≤«хорошо»<4,5. Однако рейтинговую оценку, соответствующую комбинации частных оценок, включающей оценку «удовлетворительно», вполне справедливо и необходимо откорректировать таким образом, чтобы сделать ее ниже рейтинговой оценки комбинации без частной оценки «удовлетворительно».
Так, например, в интервалах оценки «хорошо» при двух результатах оценки подготовленности специалиста – в первом случае оценка за практику 4,4 («хорошо»), за теорию 4,0 («хорошо»), а во втором случае оценка за практику 5,0 («отлично»), а за теорию 3,4 («удовлетворительно») – полученные предварительные рейтинговые оценки, средний балл которых равен 4,2, оказываются одинаковыми и по нормативным условиям оценивания соответствуют рейтинговому интервалу 3,5≤«хорошо»<4,5. Однако рейтинговую оценку, соответствующую комбинации частных оценок, включающей оценку «удовлетворительно», вполне справедливо и необходимо откорректировать таким образом, чтобы сделать ее ниже рейтинговой оценки комбинации без частной оценки «удовлетворительно».



 Как при отсутствии, так и при наличии снижающих оценок формируется только одно предварительное значение рейтинговой оценки для соответствующего диапазона рейтингового интервала оценки (для рассматриваемого примера – интервал 3,5≤«хорошо»<4,5).
Как при отсутствии, так и при наличии снижающих оценок формируется только одно предварительное значение рейтинговой оценки для соответствующего диапазона рейтингового интервала оценки (для рассматриваемого примера – интервал 3,5≤«хорошо»<4,5). (7)
(7) (8)
(8) Линейные преобразования получаемых предварительных значений рейтинговых оценок должны обеспечить такую коррекцию их значений, чтобы они не выходили за границы установленных рейтинговых интервалов. При этом, если оценки за теорию и практику окажутся не ниже 4,0 (чему соответствует R″хор1≠0 и R″хор2=0), в соответствии с (5) итоговая рейтинговая оценка специалиста должна быть в верхнем диапазоне рейтингового интервала «хорошо», а если хотя бы одна из оценок окажется ниже 4,0 (чему соответствует R″хор1=0 и R″хор2≠0), рейтинговая оценка специалиста должна быть в нижнем диапазоне рейтингового интервала (6) «хорошо».
Линейные преобразования получаемых предварительных значений рейтинговых оценок должны обеспечить такую коррекцию их значений, чтобы они не выходили за границы установленных рейтинговых интервалов. При этом, если оценки за теорию и практику окажутся не ниже 4,0 (чему соответствует R″хор1≠0 и R″хор2=0), в соответствии с (5) итоговая рейтинговая оценка специалиста должна быть в верхнем диапазоне рейтингового интервала «хорошо», а если хотя бы одна из оценок окажется ниже 4,0 (чему соответствует R″хор1=0 и R″хор2≠0), рейтинговая оценка специалиста должна быть в нижнем диапазоне рейтингового интервала (6) «хорошо».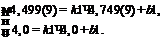 (10)
(10)

 . (12)
. (12)