При управлении компаниями, ориентированными на оказание консультационных услуг, ключевой задачей является построение оптимальных организационных структур, так как основной источник доходов и затрат – это специалисты компании. Объектом исследования является деятельность фирмы, занимающейся проектированием, разработкой, внедрением и сопровождением автоматизированных систем, предоставлением консалтинговых услуг. Компания заинтересована в наличии оптимального количества специалистов, приносящих доход своим участием в различных проектах. В то же время ей невыгодно содержать сотрудников, не задействованных в проектах, так как это приводит к убыткам (выплата должностных окладов, амортизация используемого оборудования, накладные и транспортные расходы).
Поскольку деятельность компании связана с обслуживанием клиентов на основе поступающих заявок, то есть потока дискретных событий, для решения задач планирования штата актуально применение средств компьютерного имитационного моделирования. Для решения простых, некритичных задач клиенты заинтересованы в привлечении специалистов со средним и низким профессиональным уровнем с целью сокращения затрат на обслуживание. К решению срочных задач или задач, имеющих повышенные требования к качеству, привлекаются специалисты высокого уровня. Требуемый профессиональный уровень исполнителя определяется свойствами поступающей заявки.
В обобщенной постановке задача формулируется следующим образом: компании необходимо обеспечить обслуживание поступающих заявок с максимизацией прибыли P(T) в течение заданного интервала времени T.
Введем обозначения переменных и показателей, характеризующих рассматриваемый процесс.
Q – множество обслуживаемых (сопровождаемых) компанией проектов (систем, производственных объектов).
J – множество производственных задач по обслуживаемым проектам.
Ji – i-е подмножество однотипных задач; тип производственной задачи определяется ее назначением и содержанием, соответствующим определенной профессии: программист, инженер-механик, инженер-электрик и т.п.; для решения задач каждого типа должны привлекаться специалисты соответствующей профессии; можно считать, что подмножества Ji не пересекаются, то есть справедливы выражения 
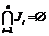 ; если рассматриваются однотипные производственные задачи, то n=1.
; если рассматриваются однотипные производственные задачи, то n=1.
Rij – уровень сложности j-й производственной задачи i-го типа; однотипные задачи могут группироваться по уровню сложности, например, если j-я и k-я задачи i-го типа имеют один и тот же уровень сложности (Rij=Rik), то они относятся к одной группе.
V – множество профессий сотрудников, выполняющих производственные функции; специалист i-й профессии обеспечивает решение множества J(Vi) типов производственных задач, при этом должно выполняться условие  .
.
В частном случае ½V½=1.
Ki – множество уровней квалификации (должностей или специализаций) сотрудников i-й профессии.
Kij – j-й уровень квалификации i-й профессии; уровнем профессиональной квалификации определяются также производительность труда и качество выполняемых работ (чем выше уровень квалификации, тем выше производительность труда и качество выполняемых работ).
Для каждой профессии vÎV установлено множество уровней квалификации специалистов Kv, ½Kv½³1, и каждому kÎKv соответствует определенное количество сотрудников Nk (плановое или фактическое), что формально можно записать следующим образом: " vÎV $ f:v®Kv½" kÎKv $ Nk½ k«Nk & NkÎ[0, 1, 2, …].
Jij – подмножество производственных задач i-го типа j-го уровня сложности, которые выполнит специалист Kij-й квалификации; между Kij и Jij может быть установлено взаимно-однозначное (Kij«Jij) или многозначное (Kij®{Ji,1, …, Ji,j-1, Ji,j}) соответствие, если специалист i-й профессии j-го уровня квалификации может выполнять работы i-го типа от первого до j-го уровня сложности включительно.
lq,ij – интенсивность поступления по q-му проекту заявок i-го типа j-го уровня сложности (Rq,ij).
vq,ij – объем работ (в часах) по заявке i-го типа j-го уровня сложности q-го проекта (Rq,ij).
Us,ij(T) – объем работ (в часах), который может быть выполнен специалистом i-й профессии j-го уровня квалификации в течение заданного интервала времени T.
Cij – цена услуг специалиста i-й профессии j-го уровня квалификации, привлеченного для выполнения работ (руб./ч); если для s-го специалиста устанавливаются индивидуальные расценки на работы, то для обозначения этого факта следует использовать дополнительный индекс, тогда следует обозначать цену как Cs,ij (руб./ч). Правила назначения цены: 1) взаимно-однозначное соответствие цены услуги и уровня сложности производственной задачи (Cij«Rij); 2) если для выполнения работы i-го типа j-го уровня сложности привлекается специалист более высокой квалификации, чем требуется, то цена услуги устанавливается в соответствии с квалификацией привлекаемого специалиста (Cs,i,j+1>Cij).
Для использования формальных правил назначения цены каждая заявка должна иметь соответствующий классификационный признак zÎZ, например:
z=1 – заявка должна обслуживаться только на основе взаимно-однозначного соответствия уровня сложности производственной задачи уровню квалификации специалиста (Kij«Jij); дополнительно может быть установлено условие ограничения продолжительности обслуживания заявки (tобсл.,q,ij£tдоп.,q,ij),
z=2 – заявка может обслуживаться специалистом более высокой квалификации; при этом стоимость услуги соответствует квалификации привлекаемого специалиста (Cs,i,j+1>Cij),
z=3 – то же, что при z=2, только дополнительно требуется минимизация продолжительности обслуживания (то есть заказчику требуется минимизация продолжительности обслуживания даже по завышенной цене); этот признак может соответствовать внеочередному обслуживанию за дополнительную плату.
Значение прибыли на k-й итерации моделируемого процесса оценивается как Pk(T)=Dk(T)–Rk(T), где Dk(T), Rk(T) – доходы и расходы за период времени Т соответственно:

lq,ij,k – количество заявок i-го типа j-го уровня сложности, выполненных по q-му проекту на k-й итерации;
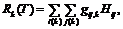
gij,k – количество сотрудников i-й профессии j-го уровня квалификации, обслуживавших заявки на k-й итерации; Hij – норматив расходов на одного сотрудника i-й профессии j-го уровня квалификации; может использоваться более детальная калькуляция расходов при наличии соответствующей математической модели.
Случайными величинами в данной модели являются интенсивность поступления заявок (lq,ij), уровень сложности (Rq,ij), объем работ по заявке (vq,ij), объем работ, который может быть выполнен специалистом в течение заданного интервала времени (Us(T) ч).
Оптимизируемым параметром, варьируемым при выполнении итераций в целях поиска наибольшего значения целевой функции P(T), является количество специалистов i-й профессии и j-го квалификационного уровня gij(T), привлекаемых на заданное время T().
Значение целевой функции процесса P(T) можно определить путем варьирования значений оптимизируемых параметров при выполнении итераций (циклов моделирования).
Количество заявок j-го типа за время T зависит от количества сопровождаемых компанией проектов и интенсивности поступления заявок на обслуживание по каждому проекту: kj(T) , где qj – количество проектов j-го типа; Mq – интенсивность поступления заявок по q-му проекту; Tq – продолжительность сопровождения q-го проекта.
, где qj – количество проектов j-го типа; Mq – интенсивность поступления заявок по q-му проекту; Tq – продолжительность сопровождения q-го проекта.
Значение целевой функции должно определяться при следующих ограничениях:
 .
.
В данной работе рассматривается модель оптимизации указанной деятельности компании для частного случая при n=1, ½V½=1, Ki=3, 
 , Kij«Jij, Cij«Rij, ½Q½£50. Оптимизируемым параметром является количество специалистов каждого из трех уровней квалификации.
, Kij«Jij, Cij«Rij, ½Q½£50. Оптимизируемым параметром является количество специалистов каждого из трех уровней квалификации.
 Для решения поставленной задачи рационально применение методики многоподходного имитационного моделирования (МИМ) [1], позволяющей объединить в одной модели различные методологии моделирования (в данном случае – дискретно-событийное и агентное).
Для решения поставленной задачи рационально применение методики многоподходного имитационного моделирования (МИМ) [1], позволяющей объединить в одной модели различные методологии моделирования (в данном случае – дискретно-событийное и агентное).
Авторами разработаны имитационная модель определенной выше деятельности, механизмы управления ее параметрами, средства сбора статистики. Средой для разработки модели выбрана система AnyLogic компании XJ Technologies, позволяющая применять МИМ с описанием различных частей гетерогенных систем и с использованием различных подходов к моделированию [2].
Разработанная модель состоит из следующих элементов:
Main – основной класс, определяющий взаимодействие объектов;
Client – класс, описывающий поведение клиентов компании (класс – агент);
Firm – класс, определяющий деятельность компании, обработку заказов;
Specialist – класс, описывающий поведение специалистов (класс – агент);
Request – класс обрабатываемой заявки (Java-класс);
Simulation – эксперимент, позволяющий выполнить имитационное моделирование при заданных параметрах;
Optimization – оптимизационный эксперимент, позволяющий вычислить оптимальные значения заданных параметров.
Процесс обслуживания заявок описывается с помощью дискретно-событийного моделирования с использованием объектов библиотеки Enterprise Library (рис. 1):
– заявки класса Request, поступающие в объект Firm, направляются на вход процесса обслуживания (enter) и далее в очередь (queue) на распределение по специалистам;
– при выходе из очереди выполняются задержка заявки (setSpecDelay) и назначение ответственного специалиста (setSpecialist); время задержки заявки распределено согласно треугольному закону
 (1)
(1)
где min=0,1; max=1; mod=0,2;
– функция setSpecialist определяет наименее загруженного компетентного специалиста по работе с типом системы, указанным в заявке, и выполняет проверку возможности передачи заявки специалисту (readyToSend); при отсутствии свободных специалистов требуемой компетенции заявка отмечается как упущенная и передается объекту sinkLost, который уничтожает ее и оповещает клиента о том, что заявка не обработана;
– если заявке был назначен ответственный за ее выполнение специалист, она пересылается (exitToSpec) соответствующему экземпляру объекта Specialists; после обработки заявка поступает на вход процесса enterFinished и передается объекту sinkFinished, который уничтожает ее и оповещает владельца заявки о том, что она обработана;
– заявки, не обработанные специалистом по каким-либо причинам (например, по истечении установленного периода обслуживания), возвращаются в процесс на вход enterLost и передаются объекту sinkLost, который их уничтожает и оповещает клиента о том, что заявка не обработана;
– если время ожидания в очереди queue превышает заданные нормативы, заявки также попадают к объекту sinkLost.
Класс Specialist является агентом, что позволяет моделировать произвольное децентрализованное поведение отдельных экземпляров объектов и их взаимодействие. Процесс обработки заявки специалистом достаточно детерминирован и моделируется с помощью инструментария дискретно-событийного моделирования (рис. 2):
– заявки Request поступают на входы процесса (enter, enterFromSpec) и передаются объекту seize, который выделяет необходимое количество ресурсов из пула (resource) и передает заявки в очередь на обслуживание (inWork); количество ресурсов в пуле (resource) моделирует возможности специалиста заниматься параллельной обработкой нескольких задач; количество ресурсов KR определяется дискретным равномерным распределением  ; в данном эксперименте принято KRÎ[1; 3], a=1, b=3;
; в данном эксперименте принято KRÎ[1; 3], a=1, b=3;
– если в пуле (resource) не хватает свободных ресурсов, заявки остаются в очереди объекта inWork и ожидают высвобождения ресурсов;
– из очереди на обслуживание (inWork) заявки передаются объекту delay, который моделирует их обработку; время обработки заявок зависит от объема работ по ним (параметр value) и коэффициента задержки, который распределен согласно треугольному закону (1) (min=0,5; max=1,5; mod=1);
– после обработки заявки (delay) ресурс (release) высвобождается и заявка возвращается в родительский процесс (exitFinished);
– если время ожидания заявки в очереди (seize, inWork) превышает установленные нормативы, она отмечается как упущенная и покидает процесс через выход exitLost.
 В случае, если специалист полностью загружен (нет свободных ресурсов в пуле resourсe) и очередь задач на обработку превышает критическое значение (параметр CriticalQueueSize), агент переходит в состояние «перегружен» и пытается передать задачи из очереди свободным агентам. Если свободный агент имеет необходимую компетенцию (параметр competence) и желание принять задачу (вероятность приема задачи равна 0,8), то она покидает очередь перегруженного агента и встает в очередь на обслуживание свободным агентом. Таким образом обеспечивается равномерное распределение задач между специалистами.
В случае, если специалист полностью загружен (нет свободных ресурсов в пуле resourсe) и очередь задач на обработку превышает критическое значение (параметр CriticalQueueSize), агент переходит в состояние «перегружен» и пытается передать задачи из очереди свободным агентам. Если свободный агент имеет необходимую компетенцию (параметр competence) и желание принять задачу (вероятность приема задачи равна 0,8), то она покидает очередь перегруженного агента и встает в очередь на обслуживание свободным агентом. Таким образом обеспечивается равномерное распределение задач между специалистами.
Для определения оптимальных значений параметров модели использовался оптимизатор OptQuest, встроенный в систему AnyLogic. Комбинируя эвристики, нейронные сети и математическую оптимизацию, OptQuest позволяет при заданных параметрах (табл. 1) находить оптимальные значения переменных модели (gij(T) – количество специалистов j-й квалификации), соответствующие максимуму целевой функции P(T).
Таблица 1
Исходные параметры модели
|
Параметр
|
Описание
|
Значение
|
|
j
|
Количество различных квалификаций специалистов
|
3
|
|
q
|
Количество обслуживаемых проектов
|
48
|
|
T
|
Моделируемый период времени, рабочих часов
|
200
|
OptQuest использует результаты поиска для самообучения, что позволяет выполнять интеллектуальный поиск следующего набора альтернатив. Если альтернатива в пространстве поиска не соответствует определенным пользователем ограничениям, она автоматически исключается и исследуются другие варианты, которые с большей вероятностью удовлетворяют требованиям.
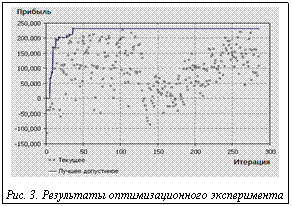 После завершения процесса оптимизации процедура OptQuest в виде графика «итерация–прибыль» (рис. 3) отображает варианты решения оптимизационной задачи и выделяет лучший из них. По оси абсцисс отложена последовательность шагов процесса поиска решения с запуском соответствующей имитационной модели. На рисунке текущие результаты изображены в виде точек, а процесс их улучшения – сплошной линией.
После завершения процесса оптимизации процедура OptQuest в виде графика «итерация–прибыль» (рис. 3) отображает варианты решения оптимизационной задачи и выделяет лучший из них. По оси абсцисс отложена последовательность шагов процесса поиска решения с запуском соответствующей имитационной модели. На рисунке текущие результаты изображены в виде точек, а процесс их улучшения – сплошной линией.
За основу стратегии выбора альтернатив взяты увеличение количества специалистов квалификации «1» (S1) и снижение количества специалистов квалификации «3» (S3). Ввиду отсутствия роста значений целевой функции системой был выбран альтернативный подход к подбору оптимизируемых параметров – уменьшение S1 и увеличение S3. Это не дало положительных результатов, а лишь привело к снижению значений целевой функции (итерации Nk=100, …, 150), так как специалисты квалификации «3» являются наименее востребованными. Система вновь сменила стратегию подбора параметров альтернатив (итерации Nk=150–290, увеличение S1 и S2 при минимальном S3). На графике наблюдается уверенный рост значений целевой функции, дисперсия достаточно мала – система определила критические параметры (S1 и S2 при минимальном S3) и начала их варьирование в узком диапазоне. Однако найденный ранее максимум показателя «прибыль» (P(T)=231320) не был превышен. Ввиду отсутствия предпосылок роста и начала снижения (итерации Nk=272–290) значений целевой функции поиск альтернатив был прекращен.
Результаты выполнения оптимизационного эксперимента позволяют сделать вывод, что при заданных параметрах (табл. 1) оптимальными являются значения, приведенные в таблице 2.
Таблица 2
Результаты моделирования
|
Переменная
|
Оптимальное значение
|
|
S1 – количество специалистов квалификации «1»
|
11
|
|
S2 – количество специалистов квалификации «2»
|
6
|
|
S3 – количество специалистов квалификации «3»
|
1
|
|
P(T) – получаемая прибыль, руб.
|
231 320
|
Применение разработанной модели дает возможность компании наиболее рационально выстраивать свои бизнес-процессы и использовать существующие ресурсы, оперативно реагировать на любые изменения в динамично развивающейся среде, повышать эффективность деятельности консалтинговой компании путем изменения состава специалистов.
Литература
1. Попков Т.В. Многоподходное моделирование: практика использования // Имитационное моделирование. Теория и практика: сб. докл. IV Всеросс. науч-практич. конф. СПб: ОАО «ЦТСС», 2009. Т. 1. С. 62–67.
2. Борщев А.В. От системной динамики и традиционного ИМ – к практическим агентным моделям: причины, технология, инструменты. URL: http://www.gpss.ru/paper/borshevarc.pdf (дата обращения: 29.03.2011).

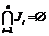 ; если рассматриваются однотипные производственные задачи, то n=1.
; если рассматриваются однотипные производственные задачи, то n=1. .
.
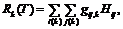
 , где qj – количество проектов j-го типа; Mq – интенсивность поступления заявок по q-му проекту; Tq – продолжительность сопровождения q-го проекта.
, где qj – количество проектов j-го типа; Mq – интенсивность поступления заявок по q-му проекту; Tq – продолжительность сопровождения q-го проекта. .
.
 , Kij«Jij, Cij«Rij, ½Q½£50. Оптимизируемым параметром является количество специалистов каждого из трех уровней квалификации.
, Kij«Jij, Cij«Rij, ½Q½£50. Оптимизируемым параметром является количество специалистов каждого из трех уровней квалификации.
 (1)
(1) ; в данном эксперименте принято KRÎ[1; 3], a=1, b=3;
; в данном эксперименте принято KRÎ[1; 3], a=1, b=3;
 После завершения процесса оптимизации процедура OptQuest в виде графика «итерация–прибыль» (рис. 3) отображает варианты решения оптимизационной задачи и выделяет лучший из них. По оси абсцисс отложена последовательность шагов процесса поиска решения с запуском соответствующей имитационной модели. На рисунке текущие результаты изображены в виде точек, а процесс их улучшения – сплошной линией.
После завершения процесса оптимизации процедура OptQuest в виде графика «итерация–прибыль» (рис. 3) отображает варианты решения оптимизационной задачи и выделяет лучший из них. По оси абсцисс отложена последовательность шагов процесса поиска решения с запуском соответствующей имитационной модели. На рисунке текущие результаты изображены в виде точек, а процесс их улучшения – сплошной линией.