Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: (evpisarenko@mail.ru) - , Ph.D | |
| Page views: 10315 |
Print version Full issue in PDF (2.00Mb) |
В работе предложена методика расчета множественности стационарных состояний режимов работы каталитических адиабатических реакторов. Созданы комплексы алгоритмов и программ «MULTIPLICITY» для нахождения областей возникновения множественности стационарных состояний в зерне катализатора и в каталитическом реакторе. Качественный анализ систем дифференциальных уравнений вышеуказанных моделей показывает, что множественность стационарных состояний может возникать за счет нелинейности кинетики химических реакций, явлений тепло- и массопереноса в грануле катализатора, а также тепловых эффектов химических реакций, протекающих в аппарате. Опубликован ряд работ (например: Froment G.F. & Bishoff K. Chemical reactor analysis and design. 1990, John Wiley &Sons, NY; Арис Р. Анализ процессов в химических реакторах. М., 1967), посвященных экспериментальному подтверждению существования множественности стационарных состояний в каталитических реакторах. Было отмечено появление гистерезиса, то есть двойственных устойчивых стационарных состояний. Явление возникновения петли гистерезиса наблюдалось при проведении экзотермических каталитических реакций за счет процессов «гашения» и «зажигания», в частности, для реакции окисления оксида углерода кислородом. Для случая Проведены детальные исследования условий возникновения множественности стационарных состояний как для экзотермических, так и эндотермических реакций. Рассмотрена кинетическая модель необратимой реакции А→B. Решения уравнений моделей проведены для случаев равных между собой диффузионных ( Уравнения материального и теплового баланса одномерной однофазной диффузионной модели каталитического реактора представимы в виде:
Граничные условия:
где В уравнения модели реактора входят факторы эффективности работы зерна катализатора как в отношении отдельных реагентов, так и реакций по маршрутам. Однако оказывается, что они не являются независимыми нелинейными функциями. В качестве базисных можно выбирать факторы эффективности только для ключевых веществ. Остальные факторы эффективности для независимых веществ и химических реакций являются только функциями от них. Так как число ключевых веществ обычно в несколько раз меньше числа независимых веществ и числа химических реакций, то тем самым задача определения факторов эффективности работы зерна катализатора существенно упрощается. Как известно, внутренние факторы эффективности работы зерна катализатора для i-го вещества и u-й химической реакции могут быть представлены в виде:
Получены соотношения, позволяющие определить концентрации неключевых веществ через концентрации ключевых веществ:
где Введем новые переменные :
Это позволяет нам преобразовать систему (1)-(5) к системе дифференциальных уравнений в безразмерных концентрациях ключевых (
Граничные условия: x=0; x=1; где сis, i=1,...,N – масштабный множитель для i-го компонента, Вычитая уравнение (10) из (9) и интегрируя результирующее дифференциальное уравнение для граничных условий (12), (13), получаем векторное уравнение реакторной стехиометрии для безразмерных концентраций реагентов:
где Вычитая уравнение (11) из (9) и интегрируя результирующее дифференциальное уравнение для граничных условий (12), (13), получим уравнение реакторного инварианта для вектора безразмерных концентраций ключевых веществ и температуры:
Уравнение (16) существенно упрощается, когда диффузионное и тепловое числа Пекле равны (
Следует заметить, что уравнения (7)-(9) должны интегрироваться неявным методом Рунге-Кутты с обратным шагом от точки x=1 к x=0. Точность интегрирования |eps|<10-6. Для интегрирования уравнений модели (9)-(11) используем уравнения реакторных инвариантов. Тогда интегрируется только одно дифференциальное уравнение (11), и алгоритм поиска множественности стационарных состояний работы адиабатического реактора складывается из следующих стадий. 1. Задаем значение Q(1) на правой границе при x=1. 2. Интегрируем справа налево уравнение (11) с использованием неявного метода Рунге-Кутты. Величины y при промежуточных значениях пространственной переменной x определяем по уравнению инварианта (17). 3. На левой границе вычисляем значение невязки e(Q(1)):
4. Методами одномерной минимизации e[Q(1)] находим
где e0 – малое число, определяемое физической сущностью задачи. Если существует несколько (нечетное количество) значений Таким образом, разработанный пакет прикладных программ «MULTIPLICITY» позволяет решить задачу оценки множественности стационарных состояний, не накладывая никаких ограничений на численное значение макрокинетических параметров модели. |
| Permanent link: http://swsys.ru/index.php?id=311&lang=en&page=article |
Print version Full issue in PDF (2.00Mb) |
| The article was published in issue no. № 4, 2007 |
Back to the list of articles
 ,
, 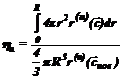 ,
, (8)
(8) . (18)
. (18)