Моделирование процесса непрерывной ферментации [1] и исследование возможности реализации оптимальных условий для процесса с нелинейной кинетикой роста от концентрации субстрата [2–5] показало следующее. Оптимальные условия по продуктивности целевого продукта определяются двумя величинами – концентрацией субстрата в поступающем потоке Sf и величиной протока D (D=Q/V, где Q – объемная скорость подачи субстрата; V – объем заполнения ферментёра). Экстремальный характер зависимости продуктивности (D×P) (P – концентрация продукта на выходе из аппарата) предполагает возможность неединственности стационарного режима, при котором одинаковое значение (D×P) может быть обеспечено различными значениями Sf и D. Это приводит к необходимости оценки показателей процесса при различных вариантах заданных условий его проведения.
Приведем разработанные алгоритмы оценки показателей процесса для следующих условий.
1. Заданы численные значения Sf и D. Необходимо оценить S, X, P и Qp=D×P.
2. Заданы допустимая область для Sf : Sfmin
3. Заданы допустимая область для D: Dmin
Особенности алгоритмов заключаются в том, что при некоторых численных значениях параметров кинетического соотношения, заданных значениях величины протока D и концентрации субстрата в поступающем потоке Sf требуется оце- нивать возможность реализации непрерывного процесса. Это означает, что при некоторых численных значениях D и Sf реализация непрерывного процесса невозможна и эти значения должны быть скорректированы. Последнее требует формулировки корректирующих соотношений и, как следствие, включения в соответствующий алгоритм диалоговой составляющей. При разработке каждого алгоритма указанные ограничения и корректирующие рекомендации включены в общую блок-схему реализации расчета показателей процесса соответствующей постановки задачи.
Разработка алгоритмов оценивания
 Алгоритм 1. Это основополагающий алгоритм, использующийся в решении других задач в различных постановках. Постановка задачи для реализации алгоритма включает задание концентрации субстрата в поступающем потоке Sf, г/л, и величины протока D, ч–1. В результате расчета необходимо получить: оценки концентрации субстрата в потоке на выходе из аппарата S, г/л; концентрации биомассы X, г/л; концентрации продукта P, г/л, и величины продуктивности Qp=D×P, г/(л×ч).
Алгоритм 1. Это основополагающий алгоритм, использующийся в решении других задач в различных постановках. Постановка задачи для реализации алгоритма включает задание концентрации субстрата в поступающем потоке Sf, г/л, и величины протока D, ч–1. В результате расчета необходимо получить: оценки концентрации субстрата в потоке на выходе из аппарата S, г/л; концентрации биомассы X, г/л; концентрации продукта P, г/л, и величины продуктивности Qp=D×P, г/(л×ч).
Блок-схема алгоритма показана на рисунке 1. Необходимые пояснения к использованию алгоритма связаны с тем, что непрерывный процесс микробиологического синтеза не всегда может быть реализован для заданных условий.
Расчетные соотношения, используемые в алгоритме, приведены в [1] и имеют вид
 , (1)
, (1)
где  , (2)
, (2)
 , (3)
, (3)
 . (4)
. (4)
Выбор знака (±) в выражении (1) определяется условием ограничения для S:
0≤S≤Sf. (5)
Знак равенства в (5) относится к предельным случаям.
Для X и P имеем
 , (6)
, (6)
P=X∙(α+β/D). (7)
Для расчета продуктивности D×P (производительности по целевому компоненту P) используем формулу D∙P=X∙(α∙D +β). (8)
Первый блок алгоритма, в котором оценивается правильность задания величины протока D при заданном Sf, требует выполнения неравенства D
Выражение для корректирующего соотношения:
 . (9)
. (9)
Если D³maxD, возможны два варианта коррекции.
1. Вычисляем maxD по заданному Sf и принимаем новое значение D
2. Вычисляем значение 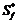 по заданному значению D:
по заданному значению D:
 .(10)
.(10)
Принимаем новое значение  .
.
Числовой пример по данным таблицы.
Пусть задано Sf=22 г/л и D=0,27 ч–1.
1. Вычисляем maxD=0,23 ч–1. Принимаем новое значение D=0,22
2. Вычисляем  =15,3963 г/л. Принимаем
=15,3963 г/л. Принимаем  . Пусть Sf=14,0 г/л. Тогда maxD=0,278 ч–1. Таким образом, D
. Пусть Sf=14,0 г/л. Тогда maxD=0,278 ч–1. Таким образом, D
Второй блок алгоритма, в котором оценивается правильность задания исходных данных Sf и D, относится к условиям соотношения знаков вспомогательных коэффициентов, а именно к условию, когда B>0 при A<0. В этом случае реализация процесса невозможна, поскольку S (концентрация субстрата в выходном потоке) принимает отрицательное значение.
Численные значения параметров
|
Yx/s, г/г
|
a, г/г
|
b, ч-1
|
mm, ч-1
|
Рm, г/л
|
Km, г/л
|
Ki, г/л
|
|
0,4
|
2,2
|
0,2
|
0,48
|
50
|
1,2
|
22
|
Возможная корректировка связана с изменением величины D до значения, при котором вспомогательный коэффициент A станет больше нуля.
Условие положительности вспомогательного коэффициента A будет иметь вид
 . (11)
. (11)
Соотношение (11) будет соотношением для корректировки D, обеспечивающей изменение знака вспомогательного коэффициента A с отрицательного на положительный.
Третий блок алгоритма, определяющий правильность задания исходных данных, включает проверку выполнения неравенства B2+4∙A∙C>0, где B<0 и A<0. Если это условие выполняется, далее следует расчет показателей процесса. Если это условие не выполняется, необходимо корректировать исходные данные.
Условие корректировки: B2+4∙A∙C>0.
Откуда
 . (12)
. (12)
Корректирующее соотношение будет иметь вид (дискриминант больше нуля)
 . (13)
. (13)
Блоки 2 и 3 на рисунке 1 обведены пунктиром. Этот фрагмент алгоритма 1 (далее модуль 1) используется в алгоритмах 2 и 3.
Алгоритм 2. Данный алгоритм является алгоритмом оптимизации, реализация которого обеспечивает возможность оценки показателей процесса S, X, P и Qp при максимальном значении продуктивности Qp=D×P.
Задание на расчет включает допустимую область выбора концентрации субстрата в поступающем потоке Sf при заданной величине прото- ка D.
Таким образом, исходные данные для расчета имеют вид a=Sf min, г/л; b=Sf max, г/л; D, ч–1.
Требуется вычислить Sf, S, X, P и Qp, при которых Qp максимальна, причем Sf min £ Sf £ Sf max.
Проверка правильности задания исходных условий для реализации непрерывного процесса и их возможная корректировка.
1. Вычисляется максимальная величина протока maxD(a) по формуле (9), где Sf=a, при которой субстрат концентрации a=Sf min полностью вымывается из аппарата, не вступив в процесс синтеза.
Если заданное значение D³maxD(a), необходимо уменьшить его.
2. Вычисляется максимальная величина протока maxD(b) по формуле (9), где Sf=b, при которой субстрат концентрации b=Sf max полностью вымывается из аппарата, не вступив в процесс синтеза.
Если заданное значение D³maxD(b), необходимо уменьшить его.
В этом условии возможна коррекция и по величине b=Sfmax. То есть вычисляется новое значение  по формуле (10) и принимается новое значение
по формуле (10) и принимается новое значение  .Таким образом, пункты 1 и 2 обеспечивают условия по заданным значениям a=Sfmin, b=Sfmax и D, при которых непрерывный процесс реализуем, то есть имеется возможность решать задачу оптимизации по критерию Qp=max.
.Таким образом, пункты 1 и 2 обеспечивают условия по заданным значениям a=Sfmin, b=Sfmax и D, при которых непрерывный процесс реализуем, то есть имеется возможность решать задачу оптимизации по критерию Qp=max.
Формула для определения Sf, отвечающего оптимальному значению Qp, имеет вид [1]

 (14)
(14)
Использование ее ограничено значением величины протока. Минимальное значение D=0, максимальное (назовем его предельным) рассчитывается по формуле
 , (15)
, (15)
где  .
.
Значения Sf при D=0 и Sf при D=Dпред и D=0 равны  . Функция (14) имеет экстремум по величине D.
. Функция (14) имеет экстремум по величине D.
Следовательно, при решении задачи максимизации Qp возможны два варианта. Первый вариант: если D
Изложенные выше положения используются в блок-схеме решения задачи оптимизации.
Однако рассматриваемая задача имеет еще ограничения, связанные с численными соотношениями a=Sf min, b=Sf max и  (когда есть возможность использовать формулу (14)).
(когда есть возможность использовать формулу (14)).
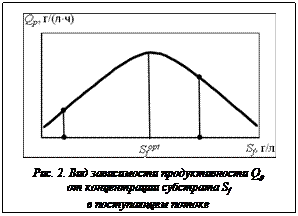
Если исходные данные или условия их корректировки выполняются, возможны следующие ситуации при определении максимальной продуктивности Qp (рис. 2):
 ; максимум Qp будет граничным, координата максимума
; максимум Qp будет граничным, координата максимума  ;
;
 ; максимум Qp будет граничным, координата максимума
; максимум Qp будет граничным, координата максимума  ;
;
 ; максимум Qp будет внутренним, координата максимума
; максимум Qp будет внутренним, координата максимума  .
.
На рисунке 3 показана блок-схема алгоритма 2.
Приведем числовой пример реализации алгоритма.
Исходные данные для расчета: a=Sf min=20 г/л; b=Sf max=30 г/л; D=0,21 ч–1.
1. Вычисляем maxD(a)=0,24376 ч–1;
D
2. Вычисляем maxD(b)=0,19970 ч–1;
D>maxD(b).
Первый вариант корректировки: принимаем новое значение D=0,18 ч–1.
3. Вычисляем предельное значение D:
Dпред=0,32718 ч–1.
Так как D=22,12022 г/л; так как выполняется условие a<22,12022=22,12022 г/л; D=0,18 ч–1.
Второй вариант корректировки:
4. Вычисляем  27,31937 г/л; принимаем b=Sf max=27 г/л (меньше
27,31937 г/л; принимаем b=Sf max=27 г/л (меньше  ).
).
5. Вычисляем maxD(b) при b=27 г/л: maxD(b)=0,21129 ч–1; D
6. Вычисляем  =19,33942 г/л.
=19,33942 г/л.
Для дальнейшего расчета условия имеют вид Sf=a=20 г/л; D=0,21 ч–1.
Значения показателей:
– по первому варианту корректировки: Qp=4,049 г/(л×ч); S=5,138 г/л; X=6,793 г/л; P=22,492 г/л;
– по второму варианту корректировки: Qp=3,741 г/(л×ч); S=5,871 г/л; X=5,652 г/л; P=17,816 г/л.
Алгоритм 3. Данный алгоритм также является алгоритмом оптимизации, реализация которого обеспечивает возможность оценки показателей процесса S, X, P и Qp при максимальном значении продуктивности Qp=D×P.
Задание на расчет включает допустимую область выбора величины протока D при заданной концентрации субстрата Sf в поступающем потоке.
 Таким образом, исходные условия для расчета имеют вид a1=Dmin, ч–1; b1=Dmax, ч–1; Sf, г/л.
Таким образом, исходные условия для расчета имеют вид a1=Dmin, ч–1; b1=Dmax, ч–1; Sf, г/л.
В результате расчета необходимо определить S, X, P, Qp и D, при котором Qp максимальна, причем Dmin£D£Dmax.
Проверка правильности задания исходных условий для реализации непрерывного процесса и возможная их корректировка.
1. Вычисляется максимальная величина протока maxD по формуле (9), при которой субстрат концентрации Sf полностью вымывается из аппарата, не вступив в процесс синтеза.
Если заданное значение b1³maxD, необходимо выполнить корректировку исходных данных. Корректировка возможна в двух вариантах. По первому варианту принимается новое значение b1, где  вычисляется по формуле (10).
вычисляется по формуле (10).
2. Вычисляется максимально возможное значение Sf, при котором можно использовать формулу (19), устанавливающую связь между Sf и D при оптимальном значении Qp.
 Максимально возможное значение Sf находится из условия
Максимально возможное значение Sf находится из условия
 . (16)
. (16)
Величина протока D по (14) может принимать значения в пределах от 0 до  . Величина Sf для этих крайних значений D равна
. Величина Sf для этих крайних значений D равна  .
.
Для максимально возможного значения Sf по формулам (14)–(16) получаем
 (17)
(17)
Отсюда
 . (18)
. (18)
Максимальное значение maxSf находится по формуле (14), где значение D вычисляется по формуле (18).
Далее, если Sf
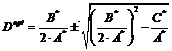 , (19)
, (19)
где  ;
;
 ;
;
 .
.
Каждому значению Sf в пределах от  до maxSf соответствуют два значения Dopt. Учитывая, что
до maxSf соответствуют два значения Dopt. Учитывая, что
 , (20)
, (20)
знак корня в (19) следует принять «+».
 Блок-схема алгоритма 3 показана на рисунке 4.
Блок-схема алгоритма 3 показана на рисунке 4.
Числовой пример реализации алгоритма 3.
Заданы следующие численные значения: a1=Dmin=0,1 ч–1; b1=Dmax=0,21 ч–1; Sf=30 г/л.
1. Вычисляем maxD по формуле (9): maxD=0,19969 ч–1.
Так как b1>maxD, то вводим корректировку по D: принимаем D=0,19 ч–1.
2. Вычисляем Dopt по формуле (19) и maxSf по формуле (14): Dopt =0,10405 ч–1; maxSf=25,8183 г/л.
3. Так как Sf>maxSf, то полагаем D=a1=0,1 ч–1.
4. Вычисляем S, X, P, Qp для D=0,1 ч–1: A=0,301629; B=2,704167; C=3,125; S=10,0011 г/л; X=8 г/л; P=33,6 г/л; Qp=D×P=3,36 г/(л×ч).
5. Полагаем D=b1=0,19 ч–1.
6. Вычисляем S, X, P, Qp для D=0,19 ч–1: A=0,190680; B=4,191042; C=11,28125; S=24,40381 г/л; X=2,24 г/л; P=7,28 г/л; Qp=1,38 г/(л×ч).
7. Так как Qp(b1)
Приведем вычисления по второй возможной корректировке.
8. Вычислим  при D=0,21 г/л:
при D=0,21 г/л:  = =27,319367 г/л.
= =27,319367 г/л.
Если в корректировке принимается значение по условию  и Sf
и Sf
9. Принимаем  и Sf
и Sf
10. Вычисляем maxD: maxD=0,224204 ч–1; D
11. Вычисляем A*, B*, C*: A*=382,05714; B*=83,50382; C*=3,77238.
12. Вычисляем Dopt по формуле (19):
Dopt=0,10928±0,04548 ч–1; D1=0,15476 ч–1; D2=0,0638 ч–1.
13. Так как a1< Dopt
14. Вычисляем показатели процесса при Dopt=0,15476 ч–1 и Sf=24 г/л: A=0,256959; B= =-0,136488; C=7,484977; S=5,1381 г/л; X=7,54 г/л; P=26,35 г/л; Qp=D×P=4,08 г/(л×ч).
Для информационного обеспечения биотехнологических процессов необходимо использовать экспериментальные исследования кинетики процессов с надежной (адекватной) математической обработкой результатов эксперимента. При этом понятно, что в силу ограниченности возможностей экспериментальных исследований они не могут быть выполнены для всей области реального существования процесса синтеза. Более того, экспериментальные исследования кинетики, как правило, проводятся в периодических условиях культивирования, и результаты не всегда могут быть перенесены на непрерывные или полупериодические условия. К тому же в большинстве случаев кинетические соотношения носят нелинейный характер, что в эксперименте часто выражается в плохой воспроизводимости его результатов. При разработке алгоритмов в данной статье эти особенности отражены в том, что в каждом алгоритме необходимо иметь диалоговую составляющую, функция которой заключается в необходимости проверки заданных условий на возможность их реализации.
Литература
1. Моделирование процессов микробиологического синтеза с нелинейной кинетикой роста микроорганизмов: учеб. пособие / Ю.Л. Гордеева [и др.]. М.: РХТУ им. Д.И. Менделеева, 2011. 100 с.
2. Agarwal P., Koshy G., Ramirez M. An algorithm for operating a fed-batch fermentor at optimum specific-growth rate. Biotechnol. Bioeng. 1989. № 33, pp. 115–125.
3. Henson M.A., Seborg D.E. Nonlinear control strategies for continuous fermenters // Chem. Eng. Sci. 1992. № 47, pp. 821–835.
4. Kumar G.P., Subrahmanya J.V.K., Chidambaram M. Periodic operation of a bioreactor with input multiplicities // Can. J. Chem. Eng. 1993. № 71, pp. 766–770.
5. McLain R.B. [et al.]. Habituating control for nonsquare nonlinear processes // Ind. Eng. Chem. Res. 1996. № 35, pp. 4067–4077.Заданы допустимая область для Sf : Sfmin

 , (1)
, (1) , (2)
, (2) , (3)
, (3) . (4)
. (4) , (6)
, (6) . (9)
. (9)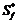 по заданному значению D:
по заданному значению D: .(10)
.(10) .
. =15,3963 г/л. Принимаем
=15,3963 г/л. Принимаем  . (11)
. (11) . (12)
. (12) . (13)
. (13) по формуле (10) и принимается новое значение
по формуле (10) и принимается новое значение  .Таким образом, пункты 1 и 2 обеспечивают условия по заданным значениям a=Sfmin, b=Sfmax и D, при которых непрерывный процесс реализуем, то есть имеется возможность решать задачу оптимизации по критерию Qp=max.
.Таким образом, пункты 1 и 2 обеспечивают условия по заданным значениям a=Sfmin, b=Sfmax и D, при которых непрерывный процесс реализуем, то есть имеется возможность решать задачу оптимизации по критерию Qp=max.
 (14)
(14) , (15)
, (15) .
. . Функция (14) имеет экстремум по величине D.
. Функция (14) имеет экстремум по величине D. (когда есть возможность использовать формулу (14)).
(когда есть возможность использовать формулу (14)). ; максимум Qp будет граничным, координата максимума
; максимум Qp будет граничным, координата максимума  ;
; ; максимум Qp будет граничным, координата максимума
; максимум Qp будет граничным, координата максимума  ;
; ; максимум Qp будет внутренним, координата максимума
; максимум Qp будет внутренним, координата максимума  .
. 27,31937 г/л; принимаем b=Sf max=27 г/л (меньше
27,31937 г/л; принимаем b=Sf max=27 г/л (меньше  Таким образом, исходные условия для расчета имеют вид a1=Dmin, ч–1; b1=Dmax, ч–1; Sf, г/л.
Таким образом, исходные условия для расчета имеют вид a1=Dmin, ч–1; b1=Dmax, ч–1; Sf, г/л.
 . (16)
. (16) . Величина Sf для этих крайних значений D равна
. Величина Sf для этих крайних значений D равна  (17)
(17) . (18)
. (18)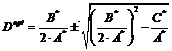 , (19)
, (19) ;
; ;
; .
. до maxSf соответствуют два значения Dopt. Учитывая, что
до maxSf соответствуют два значения Dopt. Учитывая, что , (20)
, (20)
