Software & Systems

Перспективным направлением развития современных информационных технологий являются разработка и внедрение систем поддержки принятия решений. Такие системы используются в различных сферах деятельности, но особенно востребованы там, где решаемые задачи плохо структурированы и трудно формализуемы. Для решения задач подобного рода применяются методы искусственного интеллекта: продукционные модели, нечеткая логика, искусственные нейронные сети и их комбинации [1]. Все эти задачи условно  можно разделить на две группы:

–      прямые задачи, в которых по входным данным модели процесса надо определить выходные значения  используемой модели (в частности, задачи планирования, оценки альтернативных решений);

–      обратные задачи с известными выходными значениями модели, на основании которых проводится поиск входных данных, приводящих к появлению имеющихся выходных; с точки зрения математики обратные задачи часто являются плохо поставленными, относящимися к классу некорректных задач [2].

Расширение сферы применения систем поддержки принятия решений делает востребованным поиск новых подходов к решению обратных задач, базирующихся на увеличивающихся возможностях средств вычислительной техники. Эти возможности позволяют разрабатывать и применять новые методики, например, методы на основе искусственных нейронных сетей, ранее считавшиеся чрезмерно затратными с точки зрения машинных ресурсов.

Методы решения прямых задач достаточно хорошо разработаны и изучены как соответствующие привычной постановке проблемы: есть данные на входе объекта и надо определить, что будет на его выходе, если модель объекта известна. Этого нельзя сказать про обратные задачи, методы решения которых чаще всего базируются на учете специфики предметной области. В то же время необходимость решения обратных задач (например, задач диагностики) на практике возникает достаточно часто, поэтому актуальным становится поиск новых методов и подходов к их решению.

Для обратных задач характерна ситуация, когда незначительные изменения исходных данных могут приводить к произвольно большим изменениям решений. В этих условиях для решения обратной задачи предложено использовать искусственную нейронную сеть, но на вход ей подавать данные, прошедшие процедуру фильтрации. Нейронные сети для решения обратных задач уже успешно применялись [3]. Фильтр помогает снизить уровень шумовых составляющих измерений и, как следствие, их влияние на результат решения. Из многообразия алгоритмов фильтрации был выбран фильтр Калмана, так как он позволяет использовать часть априорной информации, снижая тем самым неопределенность данных для решения обратной задачи нейронной сетью. Кроме этого, алгоритм фильтра может записываться в форме разностных уравнений, что особенно ценно при реализации их в вычислительных устройствах.

В общем случае обратную задачу можно описать следующим образом. Пусть x=G(v), где входной вектор v принадлежит множеству V, оператор G, описывающий отношения между данными и параметрами модели, представляет собой физическую систему, выходной вектор xÎ(V). В случае линейной обратной задачи, описывающей линейную систему, x=Gv. Для нелинейной обратной задачи G представляет собой нелинейный оператор, который не может быть приведен к виду линейного отображения, переводящего в данные. Задача состоит в том, чтобы по информации о векторе x определить вектор v.

Применение нейронных сетей позволяет получать решение обратных задач как для линейного, так и для нелинейного оператора G. Однако оператор G-1 должен удовлетворять требованиям теоремы о полноте, то есть быть непрерывным на замкнутом ограниченном множестве данных. В этом случае он может быть равномерно приближен функциями, вычисляемыми нейронными сетями, если функция активации нейрона дважды непрерывно дифференцируема [1]. Тогда, выбрав искусственную нейронную сеть с соответствующей структурой, можно найти решение задачи v=G-1(x) с точностью, определяемой точностью задания вектора х и оператора G.

Рассмотрим предлагаемый метод решения линейных обратных задач в постановке, характерной для теории автоматического управления. Уравнение, связывающее входной и выходной вектор,

x=Gv,                                                                        (1)

имеет решение v на V только для таких элементов x, которые принадлежат множеству GV. Предполагается, что оператор G известен точно, а вектор x обычно известен приближенно, так как представляет собой результат измерений, для которых характерно наличие векторного шума измерения N, вызывающего неточность определения x. Если u=Cx+N – это измеренное значение x, где C – матрица измерений соответствующего размера, то речь может идти лишь о нахождении приближенного к v решения уравнения C-1u=Gv, при этом u не принадлежит множеству GV. Кроме наличия шума измерений, оператор G, будучи сам непрерывным, во многих случаях не позволяет получить непрерывный обратный оператор G-1. В сложившейся ситуации в качестве приближенного решения нельзя брать точное решение (1) с приближенно заданным u, так как

–      решение может не существовать на множестве V, поскольку u может не принадлежать множеству GV;

–      решение не будет устойчивым, так как обратный оператор G-1 может не быть непрерывным. В то же время условие единственности решения обычно является следствием физической детерминированности задачи (1), и решение должно обладать этим свойством.

С другой стороны, в практических приложениях обычно требуется знать решение с некоторой точностью, поэтому можно применить метод подбора решения некорректно поставленных задач [2]: полагая, что x известен точно для элементов v некоторого заданного подкласса возможных решений Vв, (VвÎV), вычисляется оператор Gv, то есть решается прямая задача. За приближенное решение принимается такой элемент vп из множества Vв, который минимизирует невязку ρ(Gvп, x)=min ρ(Gv, x).

Построение устойчивого к малым изменениям u приближенного решения уравнения (1) по формуле v=G-1 C-1u возможно в тех случаях, когда это решение ищется на компакте MÎV и C-1uÎH=AM. Эффективных критериев, позволяющих установить принадлежность C-1u множеству H, обычно не существует, это приходится предполагать априори [2].

Устранение затруднений, связанных с неточным знанием x, осуществляется путем поиска квазирешения vкв, минимизирующего на M функционал ρ(Gvкв., C-1u)=inf ρ(Gv, C-1u), где inf – нижняя граница возможных значений функционала. Квазирешение может быть и не одно, в этом случае под ним будем подразумевать любой элемент из множества квазирешений.

Объединение приближенного метода нахождения решения обратной задачи и метода поиска квазирешения приводит к приближенному нахождению квазирешений [2], позволяющему перейти от бесконечного пространства квазирешений к пространству, содержащему конечное число приближенных квазирешений vкв.п. Квазирешение уравнения (1) может быть не единственным, а представлять собой совокупность квазирешений Т. В качестве приближения к квазирешению vкв на множестве M можно брать любой элемент vкв.п из Т, при этом

Для применения фильтра Калмана необходимо представить вектор х в виде векторно-матричного дифференциального уравнения dx/dt=Ax+s, где А – матрица системы; s – случайный процесс типа белого шума, называемый порождающим процессом. Должны быть также известны статистические характеристики процессов N, s и соответствующие начальные условия. В результате расчета фильтра определяется его коэффициент усиления К.

В предлагаемом подходе структура алгоритма решения обратной задачи будет изменяться в зависимости от того, задан оператор преобразования G точно или он точно неизвестен. Структура решения, соответствующая первому варианту, показана на рисунке 1, второму – на рисунке 2. Представленные схемы реализуют приближенный метод поиска квазирешения обратной задачи.

На рисунках введены обозначения:  – оценка вектора х; INT – интегратор; BIC (Block of an indistinct conclusion) – блок нечеткого вывода, обеспечивающий формирование матрицы А на основании внешней информации I о преобразовании G; xи, vи – значения векторов x и v, полученные на модели оператора G. Пунктирные линии обозначают, что эти связи используются на начальном этапе реализации алгоритма для обучения нейронной сети и подстройки матрицы А.

Обработка результатов измерения u проводится с применением фильтра Калмана: этот алгоритм позволяет оценивать весь вектор состояния, в то время как в результатах измерений могут присутствовать лишь некоторые его компоненты. На вход гибридной нейронной сети поступает уже не измерение u, а оценка . Выбор гибридных сетей обосновывается тем, что в них допускается не только автоматическое приобретение знаний на основе обучающих выборок, но и коррекция БЗ на основании априорной информации, которой располагают эксперты соответствующей предметной области.

Если оператор G известен точно, то, используя значения vi из заданного подкласса возможных решений Vв, (VвÎV), и решая прямую задачу, можно получить наборы соответствующих xi. Для обучения нейронной сети используется множество пар {xi, vi}, где i=1, …, m (m – объем обучающей выборки), но на вход сети подаются наборы xi, а с выхода снимаются vi. Особенностью предложенного подхода к нахождению приближенного квазирешения vкв.п обратных задач является применение гибридной нейронной сети для аппроксимации поверхности квазирешений на основании оценки  вектора x.

Если оператор G задан неточно или неизвестен, возникает проблема формирования обучающей выборки. При неточно заданном операторе можно попробовать применить описанный выше подход к формированию обучающей выборки и провести на ней обучение нейронной сети. Ответ на вопрос о допустимости неточности задания G можно будет получить после тестовых расчетов, и, если результаты устраивают исследователя, можно рекомендовать практическое применение.

Если же оператор G неизвестен, предлагается формирующий фильтр, который в данном случае будет использоваться как модель преобразования, описываемого оператором G, на входе которого вектор vи, а на выходе вектор xи. Структура формирующего фильтра известна, а значения параметров определяются на основе процедуры нечеткого логического вывода в блоке BIC, БЗ которого заполняется знаниями экспертов той предметной области, для которой решается обратная зада- ча [4].

Математически строгое обоснование такого подхода весьма громоздко, поэтому критерием допустимости его применения вновь может служить получение результатов, ценных с практической точки зрения. Рассмотрим иллюстративный пример решения обратной задачи, в котором объектом исследования будет сервомотор на постоянном токе. Входным сигналом для него выступает прилагаемое к обмоткам напряжение v(t). Ток i(t) в цепи ротора описывается соотношением v(t)= =Ri(t)+Ldi(t)/dt+s(t), где R, L – активное сопротивление и индуктивность ротора соответственно; s(t) – обратная электродвижущая сила. Эта сила, обусловленная вращением схемной рамки в магнитном поле, подчиняется зависимости s(t)=kvdη(t)/dt, где η(t) – угол поворота оси мотора. Вращающий момент на оси мотора, создаваемый током, описывается уравнением Tвр(t)=kai(t). В данных формулах kv, ka – коэффициенты пропорциональности соответствующих размерностей.

На ось также действует момент нагрузки Tнагр(t), тогда в соответствии с третьим законом Ньютона можно записать J d2η(t)/d2t=Tвр(t)– –Tнагр(t)–kтр dη(t)/dt, где J – момент инерции ротора и нагрузки; kтр – вязкое трение. Пренебрегая индуктивностью схемной рамки, L=0, можно преобразовать последнее уравнение к форме пространства состояний:

                                                     (2)

где , ,

.                                                        (3)

Полученные уравнения отражают зависимость сигналов в непрерывном времени. Но, как уже отмечалось, вычислительные алгоритмы удобнее реализовывать для дискретного времени. Поэтому осуществляется переход от описания в непрерывном времени (2) к описанию в дискретном времени. Приложим кусочно-постоянный входной сигнал и дискретизируем выходной с интервалом T. Тогда, полагая момент нагрузки равным нулю и вводя вектор , уравнение (2) для дискретного времени запишем как

x(t+T)=Aт (τ, β) x(t)+Bт (τ, β)v(t),                    (4)

где             (5)

.(6)

Далее введем оператор q сдвига вперед на Т единиц времени и перепишем (4) с учетом этого оператора:

[qE-Aт(τ, β)]x(kT)=Bт(τ, β)v(kT),                          (7)

где Е – единичная матрица.

Формула (7) позволяет окончательно записать модель в виде, соответствующем (1):

x(kT)=GT v(kT),                                                        (8)

где в данном случае GT=[qE-Aт(τ, β)]-1 Bт(τ, β).

Фактическое измерение величины угла η(t) осуществляется с ошибкой N(t), обусловленной ограниченной точностью, например, из-за градуировки шкалы измерительного прибора. Эта ошибка может быть описана последовательностью независимых случайных величин N(kT) с нулевым средним и известной дисперсией, рассчитанной по ошибкам округления в процессе измерений. Тогда модель измерений принимает вид

u(kT)=Cx(kT)+N(kT),                                       (9)

где С=(1   0).

Для проведения численного эксперимента зададимся численными значениями параметров: R=10, kv=2,5, ka=1,7, kтр=0,9, J=1,5, T=0,5. В результате расчетов по формулам (3), (5) и (6) получаем τ=1,132, β=0,128, ,

, .

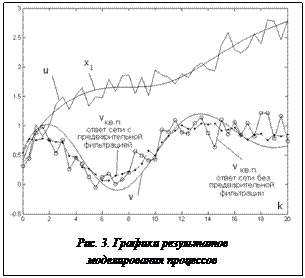Для реализации численных расчетов использовалась среда MatLAB. Сформировав в ней вектор значений сигнала v(kT) и используя (8), рассчитывается обучающая выборка для гибридной нейронной сети. Выборка содержит пары значений векторов {x(kT), v(kT)}, k=1, ..., m. Имитация процесса измерений проводилась в соответствии с (9), при этом для моделирования шума N(kT) использовался генератор псевдослучайных равномерно распределенных на интервале [0, 1] чисел. Результаты моделирования показаны на рисунке 3.

Рисунок отражает ожидаемую ситуацию, когда приближенное квазирешение vкв.п обратной задачи без предварительной фильтрации имеет большую дисперсию, чем решение, найденное при использовании фильтра Калмана. В данном примере без использования фильтрации среднеквадратичная ошибка составляет 0,21, а с фильтром получено значение 0,1657, что показывает эффективность применения предложенного подхода. Влияние относительных уровней шумов и сигналов на величину среднеквадратичной ошибки требует дополнительных исследований и экспериментов.

Предложенный подход к нахождению решений обратных задач может использоваться в различных практических ситуациях, когда достаточно получить численное, а не аналитическое решение задачи.

Литература

1. Круглов В.В., Дли М.И., Голунов Р.Ю. Нечеткая логика и искусственные нейронные сети. М.: Изд-во Физматлит, 2001. 224 с.

2. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М.: Наука, 1979.

3.  Новые возможности в  решении обратных задач лазерной спектроскопии с применением искусственных нейронных сетей / И.В. Гердова [и др.] // Изв. РАН: Сер. Физическая. 2002. Т. 66.

4. Абраменкова И.В., Пучков А.Ю., Павлов Д.А. Нейро-нечеткий метод снижения чувствительности решения обратных задач к вариациям данных // Программные продукты и системы. 2011. № 4 (96).