Journal influence
Bookmark
Next issue
Solving average delay cost routing problem
The article was published in issue no. № 3, 2013 [ pp. 202-205 ]Abstract:The article describes a flow model of an information network with alternative routing of messages to any num-ber of switching nodes and links. The authors formulate the optimization criteria for the delay posts, restrictions on the сhannel сapacity and the conservation of flows on the network. Analytical relations for information flows optimal distribu-tion in a network of three lines are recieved using the method of Lagrange multipliers. Obtained relations are extended to var-ious numbers of lines. The paper shows formulas validity tocalculate the optimal flow distribution for the specialcase of a network consisting of two lines. The calculation program inMatLab is developed. It allows for the topological network struc-ture, the input streams matrix and bandwidth to find the optimal flow distribution in the network consisting of an arbitrary number of nodes and links. The article shows an example of the input flows optimal division for a network of four nodes and three lines, providing a minimum average latency. Changing the flow optimal distribution for this example is shown with a decrease in the number of lines to two. The paper outlines approaches to the problem of flows optimal distribution with in-termediate nodes in a simulated network topology.
Аннотация:Рассмотрена потоковая модель информационной сети с альтернативной маршрутизацией сообщений для произвольного количества коммутационных узлов и каналов связи. Сформулированы критерий оптимизации по времени задержки сообщений, ограничения на пропускные способности каналов и условия сохранения потоков в сети. С использованием метода неопределенных множителей Лагранжаполучены аналитические соотношения для оптимального распределения информационных потоков в сети из трех линий связи. Полученные соотношения распространены на произвольное количество линий связи. Показана справедливость формул для расчета оптимального распределения потоков для частного случая сети, состоящей из двух линий связи. Разработана программа расчета в среде MatLab, позволяющая по топологической структуре сети, матрице входных потоков и пропускной способности каналов найти оптимальное распределение потоков в сети, состоящей из произвольного количества узлов и линий связи. Рассмотрен пример оптимального разделения входных потоков для сети из четырех узлов и трех линий связи, обеспечивающего минимум среднего времени задержки. Продемонстрировано изменение оптимального распределения потоков для рассмотренного примера при уменьшении числа линий связи до двух. Намечены подходы к решению задачи оптимального распределения потоков при наличии в топологии моделируемой сети промежуточных уз-лов.
| Authors: Margolis B.I. (borismargolis@yandex.ru) - Tver State Technical University, Tver, Russia, Ph.D, Muzanna M.M. (mohamed1984a@yahoo.com) - Tver State Technical University, Tver, Russia | |
| Keywords: the optimal routing, topology, input stream, bandwidth, the average message delay, communication channel, switching node, information network |
|
| Page views: 10596 |
Print version Full issue in PDF (13.63Mb) Download the cover in PDF (1.39Мб) |
Современные телемедицинские подходы позволяют врачам проводить удаленные консультации для пациентов, находящихся в самых от- даленных районах. Представители всех медицинских специальностей предоставляют услуги, используя инфокоммуникационные технологии, после получения информации, необходимой для диагностики, лечения и профилактики заболеваний. Инфокоммуникационные системы предполагают организацию телекоммуникационной и компьютерной сети, обеспечивающей транспорт информационных потоков и большую скорость решения задачи маршрутизации на основе балансировки нагрузки этих потоков между объектами системы. При проведении телемедицинской консультации необходимо принимать во внимание следующие особенности телемедицинских сетей (ТМС): данные критичны к задержкам при передаче, поэтому должны доставляться в реальном времени; данные теряют актуальность и становятся бесполезными, если не доставляются вовремя; неравномерность (скачкообразность) задержек при доставке отдельных пакетов информации может существенно ухудшить качество воспроизведения, поэтому должна быть минимальной. Важным направлением исследований в области передачи информации в ТМС являются анализ и решение задач, связанных с минимизацией задержки и распределением нагрузки с помощью моделей маршрутизации. Проблемы маршрутизации присутствуют как в сетях коммутации пакетов и сообщений, так и в цифровых сетях коммутации каналов. Конкретная реализация алгоритма маршрутизации существенно зависит от специфических особенностей сети, но в целом для различных сетей используется достаточно похожий математический аппарат – алгоритмы кратчайшего пути и потоковые алгоритмы, применяемые к потоковым моделям сетей, основанных на интенсивностях трафика, поступающего в линии связи. В потоковых моделях делается неявное предположение, что статистика трафика, поступающего в сеть, не меняется во времени. Такое допущение разумно, когда эта статистика меняется очень медленно по сравнению со средним временем, необходимым для уменьшения очередей в сети, и когда потоки в линиях измеряются путем временного усреднения [1]. В данной работе рассмотрена задача распределения нагрузки на основе модели маршрутизации, позволяющая уменьшить среднюю задержку пакетов в сети на основе прогноза интенсивности трафика по линиям связи, содержащим произвольное количество каналов. Рассмотрим следующую потоковую модель информационной сети с альтернативной маршрутизацией сообщений. Информационная модель состоит из n узлов коммутации и m каналов для каждой линии связи. Предполагается следующее: – все линии связи абсолютно надежны и помехоустойчивы; – узлы коммутации имеют бесконечную память; – время обработки в узлах коммутации отсутствует; – длины всех сообщений независимы и распределены по показательному закону со средним значением 1/m байт; – трафик, поступающий в сеть, состоит из сообщений, имеющих одинаковый приоритет, и образует пуассоновский поток со средним значением γij сообщений/сек. для сообщений, возникающих в узле i и предназначенных узлу j; обозначим полный внешний трафик
– пропускная способность каждой линии связи, соединяющей узлы i и j, равна dij байт/сек. или Cij=μdij сообщений/сек. Важной характеристикой качества функционирования сети является средняя задержка сообщения в сети T. Распространяя полученные Клейнроком результаты [2] на произвольное количество каналов k для каждой линии связи, получим
где fijk – суммарный поток сообщений/сек., протекающий по k-му каналу линии связи (i, j). Таким образом, задачу оптимальной маршрутизации можно сформулировать следующим образом. По заданной топологической структуре информационной сети, матрице входных потоков ||γij|| и пропускным способностям ||Cijk|| необходимо найти такие значения потоков ||fijk||, которые минимизируют среднюю задержку сообщений в сети T, то есть решить оптимизационную задачу
при выполнении ограничений:
Задача выбора оптимальных потоков в информационной сети по критерию средней задержки в случае альтернативной маршрутизации относится к классу многопродуктовых задач с выпуклой целевой функцией и выпуклым множеством ограничений. Следовательно, существует единственный локальный минимум данной задачи, являющийся глобальным минимумом, для нахождения кото- рого разработано достаточно большое число вычислительных методов [1–2]. В [1] при решении задачи оптимальной маршрутизации описаны возможности прохождения потоков только по двум каналам. Остановимся на задаче балансировки нагрузки для произвольного количества каналов аналитическими методами оптимизации. Рассмотрим простую сеть, состоящую из трех линий связи (рис. 1), формирующую поступающую нагрузку в виде бесприоритетного трафика.
с ограничением γ=f1+f2+f3. Используя метод неопределенных множителей Лагранжа [2], сформируем целевую функцию в виде
Находя частные производные по переменным f1, f2, f3, λ и приравнивая их к нулю, получим
Тогда следовательно,
По аналогии выражения оптимальных потоков для произвольного количества m линий связи будут выглядеть следующим образом:
Подразумевается, что входной поток данных меньше пропускной способности сети:
Для реализации полученных при решении задачи оптимальной маршрутизации соотношений (9) в среде MatLab разработана программа analy- tic.m, позволяющая по топологической структуре информационной сети, матрице входных потоков ||γij|| и пропускным способностям ||Cijk|| найти оптимальные потоки Пример. Рассмотрим сеть, состоящую из четырех узлов и трех линий связи (рис. 2) (1→2, 1→4, 2→3, 3→4). Известный входной поток γ требуется разделить на три путевых потока f1, f2 и f3, чтобы минимизировать целевую функцию по критерию среднего времени задержки пакетов T (см. (3)).
Результаты расчета оптимальных потоков при разделении на три канала выглядят следующим образом:
Минимальный критерий средней задержки сообщений в сети T=1,371. Очевидно, что выполняются исходные ограничения Предложенную модель оптимального распределения потоков в ТМС можно использовать для произвольного числа линий связи и узлов. Однако при наличии в топологии моделируемой сети промежуточных узлов необходимо также учитывать условия сохранения потоков для них. В этом случае для решения задачи понадобятся численные оптимизационные методы. В то же время разделение полученных оптимальных потоков по нескольким линиям связи может быть выполнено по приведенной в работе аналитической оптимизационной модели. Литература 1. Парфенов В.И., Золотарев С.В. Об одном алгоритме решения задачи оптимальной маршрутизации по критерию средней задержки // Вестн. ВГУ: сер. Физика. Математика. 2007. № 2. С. 28–32. 2. Пантелеев А.В., Летова Т.А. Методы оптимизации в примерах и задачах. М.: Высш. школа, 2005. 544 с. References 1. Parfenov V.I., Vestnik VGU, seriya: Fizika. Matematika [The bulletin of VSU. Phisics. Math series], 2007, no. 2, pp. 28–32. 2. Panteleev A.V., Metody optimizatsii v primerakh i zadachakh [Optimization methods in examples and exersises], Moscow, Vysshaya shkola, 2005. |
| Permanent link: http://swsys.ru/index.php?id=3588&lang=en&page=article |
Print version Full issue in PDF (13.63Mb) Download the cover in PDF (1.39Мб) |
| The article was published in issue no. № 3, 2013 [ pp. 202-205 ] |
Perhaps, you might be interested in the following articles of similar topics:
 ; (1)
; (1)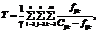 (2)
(2)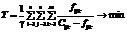 (3)
(3)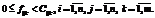 (4)
(4)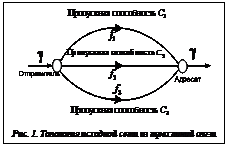 Известный входной поток γ требуется разделить на три путевых потока f1, f2, и f3 так, чтобы минимизировать целевую функцию
Известный входной поток γ требуется разделить на три путевых потока f1, f2, и f3 так, чтобы минимизировать целевую функцию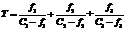 (5)
(5) (6)
(6) (7)
(7) ;
; 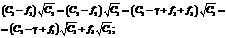

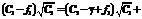
 а решение (7) выглядит следующим образом:
а решение (7) выглядит следующим образом: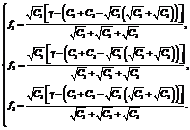 (8)
(8) (9)
(9) Полученные соотношения можно распространить на все линии связи (i, j) в (3), подставляя в (9) вместо fk и Ck соответственно fijk и Cijk. Выражение (9) справедливо для частного случая сети, состоящей из двух линий связи [1]:
Полученные соотношения можно распространить на все линии связи (i, j) в (3), подставляя в (9) вместо fk и Ck соответственно fijk и Cijk. Выражение (9) справедливо для частного случая сети, состоящей из двух линий связи [1]: (10)
(10) для произвольного количества узлов n и линий связи m.
для произвольного количества узлов n и линий связи m. Пусть входной поток
Пусть входной поток  , а пропускные способности линий связи (см. рис. 2):
, а пропускные способности линий связи (см. рис. 2): ;
;  ;
; .
. ;
; ;
;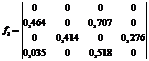 .
.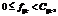
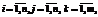 оптимизационной задачи и условия сохранения потоков в сети
оптимизационной задачи и условия сохранения потоков в сети 
 .
.