Journal influence
Bookmark
Next issue
Numerical methods for determining aircraft spatial attitude according to its 2-d optical images
Abstract:The paper presents numerical methods of determining an aircraft spatial attitude according to its optical image: namely modernized method of reference points and external contours method. In general, the task is to define a spatial position of a solid according to its central projection on a plane. Each of these methods allows receiving accurate solving the problem of determining an aircraft spatial attitude in panoramic view systems. In particular, both of the methods give the opportunity to define an aircraft spatial attitude at close distances between aircraft center and a receiving matrix. In case of automatic method of external contours such a definition is carried out in real time using standard calculating facility. The authors propose a modification of a new method of external contours in comparison with the one elaborated earlier. It is based on the transfer of all calculations from a flat physical receiving matrix to a virtual spherical receiving matrix and their automation. Practical implementation and accuracy testing of the reference points method were carried out using coordinate-measuring stand including tracking an optical channel receiving matrix. Plotting and following processing of aircraft images external contours were made using a tracking function received on the coordinate-measuring stand. There is a comparison of the experimental results obtained using the method of external contours with the results received using the method of reference points in order to determine the distance and angles of orientation of the aircraft spatial attitude. The elaborated numerical methods of determining an aircraft spatial attitude according to its optical image provides miscalculation when calculating angles of aircraft orientation: for the reference points method it is 1.5 degrees, for the external contours method it is 4 degrees. The methods are implemented as corresponding software for systems of external control and aircrafts recognition.
Аннотация:В работе излагаются численные методы определения пространственного положения летательного аппарата (ЛА) по его плоскому оптическому изображению: модернизированный метод опорных точек и метод внешних контуров. В общей постановке задача сводится к определению пространственного положения твердого тела по его центральной проекции на плоскость. Каждый из методов позволяет получить точное решение задачи определения пространственного положения ЛА в системах панорамного обзора. В частности, оба эти метода позволяют определить пространственное положение ЛА на близких расстояниях между центром ЛА и приемной матрицы. При этом в случае автоматического метода внешних контуров такое определение удается осуществить в реальном времени на стандартной вычислительной аппаратуре. Предложена модификация нового метода внешних контуров по сравнению с ранее разработанными, заключающаяся в переводе и автоматизации всех вычислений с плоской физической приемной матрицы на виртуальную сферическую приемную матрицу. Практическая реализация и проверка точности метода опорных точек были осуществлены на координатно-измерительном стенде, включая трассировку приемной матрицы оптического канала. Построение и последующая обработка внешних контуров изображений ЛА осуществлялись при помощи функции трассировки, полученной на координатно-измерительном стенде. Сравниваются результаты экспериментов, полученных по методу внешних контуров, с результатами, полученными по методу опорных точек, по оценке точности определения расстояния и углов ориентации пространственного положения ЛА. Разработанные численные методы определения пространственного положения ЛА по его плоскому оптическому изображению обеспечивают значения ошибок при вычислении углов ориентации ЛА: для метода опорных точек – 1,5 градуса, для метода внешних контуров – 4 градуса. Методы реализованы в качестве соответствующих программных продуктов для систем внешнего контроля и распознавания ЛА.
| Authors: Mirzoyan А.S. (amspectre@gmail.com) - P.A. Solovyov Rybinsk State Aviation Technical University, Rybinsk, Russia, Malyshev O.V. (omalyshev-2004@yandex.ru) - P.A. Solovyov Rybinsk State Aviation Technical University, Rybinsk, Russia, Ph.D, Khmarov I.M. (khmarov314@mail.ru) - Research Center of the Central Research Institute of Air and Space Defense Troops of Ministry of Defense of Russia, Tver, Russia, Ph.D, Meshkov V.V. (msf-tgtu@efndex.ru) - Tver State Technical University, Tver, Russia, Ph.D, Shakhov S.V. (svshahov@yandex.ru) - Tver State Technical University, Tver, Russia | |
| Keywords: aircraft, external contour, spatial position, pattern recognition, software product, 2d approximation |
|
| Page views: 14550 |
Print version Full issue in PDF (8.21Mb) Download the cover in PDF (1.09Мб) |
Определение пространственного положения летательного аппарата (ЛА) внешними оптическими системами [1, 2] имеет важное значение при обеспечении посадки самолетов в сложных метеоусловиях с помощью внешнего контроля со стороны диспетчерских служб, дистанционного управления полетом и посадкой беспилотных ЛА, реализации внешнего управления ЛА при возникновении нештатных ситуаций, расчета угловой ориентации ЛА-мишеней при испытаниях оптико-электронных систем [3], работы систем автоматического распознавания ЛА [4–6]. В свою очередь, системы автоматического распознавания ЛА актуальны для решения задач контроля воздушного пространства международными миссиями в горячих точках, документирования ситуаций в небе военными корреспондентами и очевидцами, оснащенными видеоаппаратурой, документирования ситуаций в небе в приграничных районах, контроля воздушного пространства системами оборонного назначения [7]. В задачу определения пространственного положения ЛА по его 2D-неоднородному изображению [8–10] входит получение трех линейных координат центра X, Y, Z и трех угловых координат ориентации ψ, υ, γ в заданной системе отсчета. При этом происходит сравнение реального и моделируемого [11, 12] оптических изображений ЛА. В работах [7, 13] был изложен метод определения набора линейных и угловых координат (X, Y, Z, ψ, υ, γ) по набору наблюдаемых параметров (ρ, x, y, k, t, r), снимаемых с внешнего контура G изображения ЛА на приемной матрице (ПМ). При этом внешний контур G представляет собой замкнутую ломаную, проходящую через вершины пикселей ПМ [13, 14]. В методе наблюдаемых параметров расстояние ρ определяется из соображений подобия, в качестве точки (x, y) проекции центра ЛА на ПМ принимается центр масс области, заключенной внутри контура G, а определение углов поворота r, t, k основано на минимизации невязки площадей между реальным и эталонными контурами [7, 13, 15]. Определенным недостатком данного подхода является неточность вычисления проекции (x, y) центра ЛА на ПМ. При существенных расстояниях между центром ЛА и ПМ относительная ошибка вычислений невелика. Однако при расстояниях между центром ЛА и ПМ порядка размеров ЛА относительная ошибка вычислений возрастает. В конечном счете это не позволяет определять пространственные положения ЛА при помощи метода наблюдаемых параметров на близких расстояниях [6]. В предлагаемой работе излагаются два численных метода определения пространственного положения ЛА по его плоскому изображению: модернизированный метод внешних контуров и метод опорных точек. Блок-схема данных методов, реализованных в качестве соответствующих программных продуктов для систем внешнего контроля и распознавания ЛА [7], представлена на рисунке 1. В общей постановке задача заключается в определении пространственного положения твердого тела по его центральной проекции на плоскость. Принципиальная возможность решения данной задачи основывается на следующем соображении. Минимальным невырожденным твердым телом является треугольник. Пространственное положение треугольника как твердого тела задается шестью параметрами. Центральная проекция треугольника на плоскость также задается шестью параметрами – координатами проекций его вершин. Остается определить шесть неизвестных параметров через шесть известных. Эта процедура реализуется в предлагаемом автоматизированном методе опорных точек. В предлагаемом автоматическом методе внешних контуров шестерка неизвестных параметров определяется через внешний контур центральной проекции. Модификация нового метода внешних контуров по сравнению с ранее изложенным в работе [13] заключается в переводе всех вычислений с плоской физической ПМ на виртуальную сферическую ПМ. Каждый из новых двух методов позволяет получить точное решение задачи определения пространственного положения ЛА в системах панорамного обзора [16, 17]. В частности, оба эти метода позволяют определить пространственное положение ЛА на близких расстояниях между центром ЛА и ПМ. При этом в случае автоматического метода внешних контуров такое определение удается осуществить в реальном времени на стандартной вычислительной аппаратуре [7, 13]. Метод опорных точек Численная реализация метода опорных точек основана на решении задачи определения положения пространственного треугольника. Рассмотрим пространственный треугольник с вершинами Q1, Q2, Q3 и длинами сторон r1, r2, r3, изображенный на рисунке 2. Обозначим через V1, V2, V3 проекции точек Q1, Q2, Q3 на единичную сферу. Очевидно, для некоторых t1, t2, t3 имеют место соотношения Зададим скалярные произведения s1= (V1, V2), s2= (V2, V3), s3= (V3, V1). Тогда После исключения неизвестных t2 и t3 получаем уравнение восьмой степени относительно неизвестной t1 вида Очевидная замена Проиллюстрируем метод опорных точек на конкретном примере. Пусть основные опорные точки Q1, Q2, Q3 установлены на носу и размахах крыла, а контрольные опорные точки Q4 и Q5 установлены на размахах горизонтальных стабилизаторов, как слева на рисунке 3. По конструкции ЛА определим расстояния между основными опорными точками: Оценка точности метода опорных точек Проверка точности метода опорных точек была осуществлена на координатно-измерительном стенде, изображенном на рисунке 4. Основными элементами конструкции являются параллельные направляющие, платформа оптического канала и платформа поворотного механизма. Среднее расстояние от оптического канала до центра масштабной модели ЛА задается расстоянием между платформами оптического канала и поворотного механизма. Угловые координаты рыскания ψ, тангажа υ и крена γ пространственного положения масштабной модели ЛА задаются вращением осей поворотного механизма, изображенного справа на рисунке 3. С целью практической реализации метода опорных точек производится трассировка ПМ оптического канала. Суть трассировки в том, что в системе координат оптического канала каждому пикселю p ПМ ставится в соответствие единичный вектор V(p), такой, что все точки луча с началом p и направлением V(p) оптическая система переводит в пиксель p. В лабораторных условиях операция трассировки ПМ осуществляется на платформе оптического канала, как на рисунке 5. С целью трассировки делаются два снимка масштабно-координатной сетки, расположенной в плоскостях A и B на расстоянии L в системе координат XYZ. Искомые направления V(p) строятся в результате совмещения снимков. Было проведено 100 экспериментов по определению угловых координат рыскания, тангажа и крена для физической модели ЛА типа транспортного самолета, выполненной в масштабе 1:144. В проведенных экспериментах среднее расстояние между центрами модели и оптического канала было 2 250 мм, что при масштабе 1:144 соответствует среднему расстоянию 324 м. ПМ оптического канала имела размеры 720´576 пикселей. В каждом эксперименте при помощи поворотного механизма задавались углы рыскания ψ0, тангажа υ0 и крена γ0 модели ЛА в диапазонах 5£ψ0£45, 5£J0£15, 10£γ0£60. Изображение модели через оптический канал вводилось в компьютер. Далее на изображении устанавливались три основные и одна контрольная опорные точки, как на рисунке 3. По пиксельным координатам опорных точек вычислялись углы рыскания y, тангажа υ и крена g. Затем производилось сравнение вычисленных углов y, υ и g с установленными углами y0, υ0 и g0. Статистика значений ошибок измерения Dy = y – y0, DJ = = J – J0, Dg = g – g0 в градусах приведена в таблице 1. Таблица 1 Статистика ошибок измерения угловых координат Table 1 Error statistics for angular coordinates measurement
В данной серии из 100 экспериментов наблюдаются систематические ошибки по рысканию порядка 1,5 градуса и тангажу порядка 1,2 градуса. Исключение систематических ошибок доводит среднюю ошибку по всем угловым координатам до 0,5 градуса. Основной вывод, который можно сделать из проведенных экспериментов, заключается в том, что на дальностях до 500 м метод опорных точек позволяет получать значения углов рыскания, тангажа и крена ЛА со средней точностью 1,5 градуса. Метод внешних контуров В отличие от метода [1] в настоящей работе построение и последующая обработка внешних контуров изображений ЛА осуществляются не на плоской физической, а на виртуальной сферической ПМ, показанной на рисунке 6. При этом переход от плоской к сферической ПМ осуществляется при помощи функции трассировки V(p), о построении которой уже говорилось. На рисунке 6 через 0XYZ обозначена система координат оптического канала, у которой начало 0 находится в оптическом центре, орт X идет по отрицательному направлению оптической оси, орт Y идет по столбцам, а орт Z идет по строкам ПМ. Через P0X0Y0Z0 обозначена связанная система координат ЛА, у которой начало P0 расположено на строительной оси, орт X0 идет к носу, орт Y0 идет по хвосту, а орт Z0 идет на правое крыло. Через p обозначено расстояние между оптическим центром и центром ЛА. Через Q0 обозначена точка пересечения оси 0P0 с единичной сферой с ортами Q0Y и Q0Z, идущими по местной параллели и меридиану. Важно заметить, что при повороте пространства на угол азимута α и угол превышения β орты Y и Z переходят в орты Q0Y и Q0Z. Через k обозначен угол поворота пространства вокруг оси 0P0. Угол k играет роль крена. Будем называть приведенным пространственное положение ЛА, при котором центр P0 находится на отрицательной полуоси оси 0X, а орт Y0 располагается в верхней полуплоскости плоскости 0XY, как на рисунке 7. Семейство приведенных положений ЛА задается тройкой параметров (p, t, r), где p определяет точку
Пусть ЛА находится в произвольном пространственном положении, как на рисунке 6. Тогда существует такая тройка углов (α, β, k) поворота, при которых ЛА переходит в приведенное положение. При этом изображение ЛА на сферической ПМ останется геометрически идентичным. Это позволяет при определении пространственного положения ЛА ограничиться трехпараметрическим семейством эталонных изображений, порождаемых приведенными положениями.
Пусть ЛА находится в приведенном положении, соответствующем параметрам (p, t, r). Построим внешний контур ГP изображения ЛА на плоской ПМ. С помощью функции трассировки V(p) преобразуем внешний контур ГP в замкнутую кривую ГS на сферической ПМ. Обозначим через A проекцию на единичную сферу центра масс области, заключенной внутри кривой ГS, на единичной сфере. Построим в точке A касательную плоскость П к единичной сфере с ортами АZ и AY, идущими по параллели и меридиану. Обозначим через Г центральную проекцию кривой ГS с единичной сферы на плоскость П, а через Δ пересечение оси 0X с плоскостью П. Семейство эталонных объектов (А, Г, Δ), зависящих от параметров (p, t, r), позволяет получить точное решение задачи определения пространственного положения ЛА в идеальном случае, когда внешний контур изображения ЛА не возмущен помехой. В реальном случае наличия помех пространственное положение определяется с ошибкой, оценка величины которой будет осуществлена путем сравнения с более точным методом опорных точек. Изложим алгоритм метода внешних контуров. Рассмотрим ЛА в произвольном пространственном положении, как на рисунке 6. Построим внешний контур Г0P изображения ЛА на плоской ПМ. С помощью функции трассировки V(p) преобразуем внешний контур Г0P в замкнутую кривую Г0S на сферической ПМ. Построим проекцию A0 на единичную сферу центра масс области, заключенной внутри кривой Г0S. Построим в точке A0 касательную плоскость П0 к единичной сфере с ортами A0Z и A0Y, идущими по местным параллели и меридиану. Обозначим через Г0 центральную проекцию кривой Г0S с единичной сферы на плоскость П0. Очевидно, что для некоторых параметров (p, t, r) существует такой угол поворота θ вокруг центра A0, при котором эталонная кривая Г(p, t, r) совпадет с кривой Г0. Поворачивая вокруг центра A0 точку Δ(p, t, r) на угол θ, получаем точку Δ0 пересечения оси 0P0 с плоскостью П0. Проекция точки Δ0 на единичную сферу дает точку Q0, по которой вычисляются углы азимута α и превышения β. Поясним вычисление угла k поворота вокруг оси 0P0. В случае A(p, t, r) ≠ –(1, 0, 0) зададим матрицу поворота M = [Q0 Q0Z Q0Y] и точку A1 = M*A0, где звездочкой обозначена операция транспонирования. Точки A1 и A(p, t, r) располагаются на единичной сфере в некоторой плоскости, перпендикулярной оси 0X. В качестве угла k берется угол поворота от точки A(p, t, r) к точке A1. В случае A(p, t, r)= –(1, 0, 0) задаем k=–q. Набор трех эталонных параметров A(p, t, r) и трех вычисленных параметров (α, β, k) позволяет определить вектор (x, y, z, ψ, υ, γ) пространственного положения ЛА. При практической реализации изложенного метода используются два приема, существенно уменьшающие степень перебора на этапе построения тройки эталонных параметров (p, t, r). Во-первых, запись семейства эталонных объектов (А, Г, Δ) осуществляется при характерном расстоянии p0, при этом текущее расстояние p определяется из соображений подобия. Это сводит задачу к четырем вычисляемым параметрам (p, α, β, k) при двух эталонных параметрах (t, r). Во-вторых, после предварительной записи семейства эталонных объектов (А, Г, Δ) с параметрами (t, r) в этом семействе строится e-сеть по метрике Никодима, на которой далее решается задача приближения контура изображения реального ЛА эталонными контурами. Алгоритм рационального вычисления метрики Никодима излагается в работе [5]. Пример совмещения реального (тонкая кривая) и эталонного (жирная кривая) контуров показан на рисунке 8. Оценка точности метода внешних контуров Изложим результаты экспериментов по оценке точности определения расстояния и углов ориентации пространственного положения ЛА. Точность определения расстояния проверялась на модели истребителя, выполненной в масштабе 1:72. Точность определения углов ориентации проверялась на модели транспортного самолета, выполненной в масштабе 1:144. Определение расстояния. В данных экспериментах модель истребителя подвешивалась на тонкой нити, обеспечивающей равномерное вращение вокруг центра связанной системы координат, как на рисунке 9. В первом эксперименте модель ЛА была подвешена на расстоянии 2080 мм от оптического центра, что составляет p=150 м до реального ЛА. Во втором эксперименте модель ЛА была подвешена на расстоянии 2780 мм от оптического центра, что составляет p=200 м до реального ЛА. Типичные положения модели ЛА в первом и втором экспериментах показаны слева и справа на рисунке 9. Результаты первого и второго экспериментов даны сверху и снизу на рисунке 10. В первом эксперименте были обработаны 520 кадров, во втором – 460. На графиках расстояний кадры с качественными изображениями, при которых рассогласования между эталонным и реальным контурами принимали значения μ≤0,3 по метрике Никодима, отмечены точками, сливающимися в горизонтальные отрезки из-за большого количества кадров. В первом эксперименте на качественных кадрах при μ≤0,3 получаем среднее Определение углов поворота. В данных экспериментах модель транспортного самолета совершала ускоренное движение по наклонной нити, имитируя прилет ЛА по нисходящей траектории, как на рисунке 11. Сравнение эффективности двух методов Сравнение результатов, полученных по методу внешних контуров и по методу опорных точек, для 19 контрольных кадров приведено в табли- це 2. Здесь через Δψ, Δυ, Δγ обозначены невязки между указанными методами. Таблица 2 Расхождение метода внешних контуров с методом опорных точек Table 2 Angular closing error of external contours and reference points methods
Сравнение таблиц 1 и 2 приводит к следующему выводу. Средняя величина ошибок метода опорных точек при вычислении углов рыскания, тангажа и крена имеет порядок 1,5 градуса. В свою очередь, среднее отклонение метода внешних контуров от метода опорных точек имеет порядок 2,5 градуса, поэтому средняя величина ошибок метода внешних контуров при вычислении углов рыскания, тангажа и крена имеет порядок 4 градуса. Таким образом, авторами предложены усовершенствованные численные методы определения пространственного положения ЛА по его плоскому оптическому изображению: модернизированный метод опорных точек и метод внешних контуров. Каждый из методов позволяет получить точное решение задачи определения пространственного положения ЛА в системах панорамного обзора. В частности, оба эти метода позволяют определить пространственное положение ЛА на близких расстояниях между центром ЛА и ПМ. При автоматизации метода внешних контуров такое определение удается осуществить в реальном времени на стандартной вычислительной аппаратуре. Предложена модификация нового метода внешних контуров по сравнению с ранее разработанными, заключающаяся в переводе всех вычислений с плоской физической ПМ на виртуальную сферическую ПМ и их автоматизацию. Осуществлены практическая реализация и проверка точности метода опорных точек на координатно-измерительном стенде. Построение и последующая обработка внешних контуров изображений ЛА проводились при помощи функции трассировки, полученной на координатно-измерительном стенде. Разработанные численные методы определения пространственного положения ЛА по его плоскому оптическому изображению обеспечивают значения ошибок при вычислении углов ориентации ЛА: для метода опорных точек – 1,5 градуса, для метода внешних контуров – 4 градуса. Это в 2–5 раз меньше, чем с помощью известного метода [13] и его аналогов. Данные методы реализованы в качестве соответствующих программных продуктов для систем внешнего контроля и распознавания ЛА [7]. В числе направлений для дальнейших исследований – разработка и реализация автоматических систем определения ориентации и распознавания ЛА по его 3D-изображениям [18–21], реализация методов определения пространственного положения в неблагоприятных локационных условиях и для сложных локационных сигналов. Литература 1. Steinvall O. Review of laser sensing devices and systems. Proc. of SPIE, 2005, vol. 5989, pp. 598903-1. 2. Molebny V., Zarubinb P., Kamerman G. The dawn of optical radar: a story from another side of the globe. Proc. of SPIE, 2010, vol. 7684, pp. 76840B-1. 3. Хмаров И.М., Мешков В.В., Вишняков А.С., Ша- хов С.В. Применение оптических имитаторов летательных аппаратов для обеспечения экологической безопасности испытаний оптико-электронных систем на открытых трассах // Актуальные процессы безопасности жизнедеятельности и экологии: тр. Междунар. науч.-практич. конф. Тверь: Изд-во ТвГТУ, 2015. С. 94–98. 4. Kuvich G. Target detection and identification with a scene understanding system based on network-symbolic models. Proc. of SPIE, 2005, vol. 5811, pp. 1–14. 5. Bovenkampa E., Schutte K. Laser gated viewing: an enabler for automatic target recognition. Proc. of SPIE, 2010, vol. 7684, pp. 76840Z-1. 6. Morris H., De Pass M.M. Target classifications using Scale Spaces. Proc. of SPIE, 2006, vol. 6239, 623904 (1–9). 7. Мирзоян А.С., Малышев О.В., Хмаров И.М., Кани- вец В.Ю. Распознавание летательных аппаратов оптической системой в реальном масштабе времени // Вестн. МАИ. 2014. Т. 21. № 5. С. 145–156. 8. Dills A.N., Gustafson S.C., and Perram G.P. Detonation discrimination and feature saliency using a near-infrared focal plane array and a visible CCD camera. Proc. of SPIE, 2005, vol. 5811, pp. 123–132. 9. Cordray J., Watson E., Anisimov I., Korotkova O. Speckle-field simulator characterization. Proc. of SPIE, 2009, vol. 7200, pp. 72000Q-1. 10. Bevan E.J., DiDomenico J., Briggs M., Strom C., Gedridge B. An emissivity imaging camera (eCAM) for evaluating changes in aircraft coatings. Proc. of SPIE, 2005, vol. 5811, pp. 56–66. 11. Хмаров И.М., Канивец В.Ю., Прохоров А.В., Прохо- ров В.А., Кондрашов Н.Г. Информационно-расчетные систе- мы для определения лазерно-локационных характеристик объектов // Программные продукты и системы. 2010. № 4. С. 140–142. 12. Savage J., Coker C., Thai B., Aboutalib O., Pau J. Irma 5.2 multi-sensor signature prediction model. Proc. of SPIE, 2008, vol. 6965, pp. 69650A-1. 13. Малышев О.В., Вишняков А.С., Хмаров И.М., Кондрашов Н.Г. Определение пространственных положений летательных аппаратов по их двумерным динамическим изображениям // Вестн. МАИ. 2011. № 4. C. 93–101. 14. Фурман Я.А. Введение в контурный анализ и его приложения к обработке изображений и сигналов. М.: Физматлит, 2002. 592 с. 15. Грюнбаум Б. Этюды по комбинаторной геометрии и теории выпуклых тел. М.: Наука, 1971. 96 с. 16. Chrzanowski K. Testing Thermal Imagers. Practical guidebook. Poland, Warsaw, Military University of Technology. 2010, pp. 164. 17. Gerald C. Holst G.H. Testing and Evaluation of Infrared. Imaging Systems, 3rd ed. JCD Publishing and SPIE Press, 2008, pp. 392. 18. Molebny V., Kamerman G., Steinvall O. Laser radar in a system perspective. Proc. of SPIE, 2011, vol. 8037, pp. 803709-1. 19. Mamanakis M.T., Fullmer R.R., Pack R.T., Budge S. Active and attentive LADAR scanning for automatic target recognition. Proc. of SPIE, 2008, vol. 6971, pp. 69710I-1. 20. Korotkova O., Gbur G. Propagation of beams with any spectral, coherence and polarization properties in turbulent atmosphere. Proc. of SPIE, 2007, vol. 6457, pp. 64570J-1. 21. Youmans D.G. Waveform comparison for coherent LADAR imaging using a helicopter facet model target. Proc. of SPIE, 2009, vol. 7323, pp. 732304-1. |
| Permanent link: http://swsys.ru/index.php?id=4025&lang=en&page=article |
Print version Full issue in PDF (8.21Mb) Download the cover in PDF (1.09Мб) |
| The article was published in issue no. № 3, 2015 [ pp. 33-41 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Выделение и анализ скелетов объектов на цветных снимках
- Программное обеспечение для автоматизированного обнаружения и оценки разрушений соединительных швов зданий
- Разработка прототипа информационно-технологического процесса обработки информации с учетом его стоимости
- Система автоматического картографирования знаков дорожного движения
- Программное обеспечение для сбора, обработки и передачи данных о техническом состоянии поверхности коллектора электродвигателя
Back to the list of articles








 сводит задачу к уравнению четвертой степени
сводит задачу к уравнению четвертой степени 
 , допускающему точное решение в радикалах. Явные выражения коэффициентов данного уравнения через параметры r = (r1, r2, r3) и s = (s1, s2, s3) достаточно громоздки и в настоящей работе не приводятся.
, допускающему точное решение в радикалах. Явные выражения коэффициентов данного уравнения через параметры r = (r1, r2, r3) и s = (s1, s2, s3) достаточно громоздки и в настоящей работе не приводятся.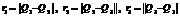 . Справа на рисунке 3 дано изображение ЛА, на котором человеком-оператором установлены три основные опорные точки p1, p2, p3 и одна видимая контрольная опорная точка p5. По пиксельным координатам p1, p2, p3 определяются единичные векторы V1, V2, V3, позволяющие получить возможные пространственные положения треугольника с длинами сторон r1, r2, r3. Выбор правильной ветви решения осуществляется при помощи видимой контрольной опорной точки. В данном примере такой контрольной опорной точкой является точка p5.
. Справа на рисунке 3 дано изображение ЛА, на котором человеком-оператором установлены три основные опорные точки p1, p2, p3 и одна видимая контрольная опорная точка p5. По пиксельным координатам p1, p2, p3 определяются единичные векторы V1, V2, V3, позволяющие получить возможные пространственные положения треугольника с длинами сторон r1, r2, r3. Выбор правильной ветви решения осуществляется при помощи видимой контрольной опорной точки. В данном примере такой контрольной опорной точкой является точка p5.


 , а два угла (t, r), играющие роль углов тангажа и рыскания, определяют матрицу поворота:
, а два угла (t, r), играющие роль углов тангажа и рыскания, определяют матрицу поворота: .
..jpg)


 =150,6 м и среднее квадратическое отклонение σ(p)=7,1 м. При истинном значении расстояния p=200 это дает относительную погрешность 4,71 % определения расстояния. Во втором эксперименте на качественных кадрах при μ≤0,3 получаем среднее значение
=150,6 м и среднее квадратическое отклонение σ(p)=7,1 м. При истинном значении расстояния p=200 это дает относительную погрешность 4,71 % определения расстояния. Во втором эксперименте на качественных кадрах при μ≤0,3 получаем среднее значение 
