Journal influence
Bookmark
Next issue
Speaker clustering using enhanced self-organizing incremental neural networks
Abstract:The paper describes the use of an unsupervised learning method based on self-organizing incremental neural networks for the problem of speaker clustering. I uses a set of mel-frequency cepstral coefficients as a user model. This set is obtained by applying a special filter to the sound signal frequency, which was transferred into the mel-frequency scale ("mel is an abbreviation of “melody”). The main difference of this work is the consideration of the dynamics of mel-frequency cepstral coefficients changing, which also contains information about the user. The possibility of new unique users emergence in the system while operating makes it impossible to use the major-ity of neural network classes, because learning on a new data set will lead to malfunction, “forgetting” of prior learn-ing. Neural networks for on-line learning impose a limit on the maximum number of clusters, that is unknown for this problem, and, in general, they require a priori knowledge of the input data (to establish thresholds, etc.) that is difficult to achieve in practice. Self-organizing incremental neural networks allow lifetime learning, that means learning during the operation stage, and do not require any a priori knowledge about the users or their quantity. A dynamic neural net-work structure makes it possible to create an unlimited number of new clusters for new previously unregistered users. Thus, this method allows building a flexible speaker clustering system that adapts itself to the changing input data.
Аннотация:В данной работе рассматривается применение метода обучения без учителя на основе самоорганизующихся растущих нейронных сетей для задачи кластеризации пользователей по голосу. В качестве модели пользователя в статье используется набор мел-частотных кепстральных коэффициентов. Данный набор получается путем применения фильтра специального вида к частоте звукового сигнала, переведенной в мел-частотную шкалу. Основным отличием данной работы является учет динамики изменения мел-частотных кепстральных коэффициентов, которая также со-держит информацию о пользователе. Возможность появления новых уникальных пользователей в процессе функционирования системы делает невозможным использование многих классов нейронных сетей, так как обучение сети на новом наборе данных приведет к нарушению функционирования, «забыванию» результатов предыдущего обучения. Нейронные сети для интерактивного обучения накладывают ограничение на максимальное количество кластеров, которое неизвестно для данной задачи, и в общем случае требуют некоторого априорного знания входных данных (для установления пороговых значений и т.д.), которое сложно обеспечить на практике. Самоорганизующиеся растущие нейронные сети позволяют производить обучение на этапе всего функционирования системы, не требуют априорных знаний ни о пользователях, ни об их количестве. Динамическая структура нейронной сети позволяет создавать неограниченное число новых кластеров при появлении новых уникальных пользователей. Таким образом, данный метод позволяет построить гибкую систему кластеризации пользователей по голосу, адаптирующуюся под изменяющиеся входные данные.
| Authors: Vagin V.N. (vagin@appmat.ru) - National Research University “MPEI”, Moscow, Russia, Ph.D, Ganishev V.A. (v.ganishev@ gmail.com) - National Research University “Moscow Power Engineering Institute”, Moscow, Russia | |
| Keywords: growing neural networks, learning phase of the neural network, learning without a teacher, mel frequency cepstral coefficients (mfcc), clusterization, feature matching, time series, adaptation |
|
| Page views: 10882 |
Print version Full issue in PDF (8.21Mb) Download the cover in PDF (1.09Мб) |
Кластеризация пользователей по голосу – разделение голосовых записей по классам таким образом, чтобы в каждом классе были аудиозаписи лишь одного пользователя. Каждая запись содержит голос только одного пользователя. Чаще всего процесс кластеризации проходит без непосредственного контроля и является составной частью задач распознавания речи и распознавания пользователей по голосу.
Кластеризация пользователей по голосу находит применение при анализе теле- и радиотрансляций, записей конференций и телефонных переговоров. Создание отдельной модели каждого пользователя весьма ресурсоемко, когда речь идет о массовых событиях и системах, содержащих тысячи записей сотен пользователей: системы в таком случае смогут работать лишь на предопределенном множестве пользователей, что лишает их гибкости и часто нецелесообразно с точки зрения экономии ресурсов. В последние годы задача автоматической об- работки речи является одним из приоритетных направлений таких областей исследований, как анализ сигналов, компьютерная безопасность и искусственный интеллект. Интерес научного сообщества в этой области поддерживается Национальным институтом стандартов и технологий (National Research of Standards and Technology, NIST), который разработал методику оценки качества систем автоматической обработки речи (Rich Transcription Evaluation Project, RTE) [1]. Для решения этой задачи часто применяются следующие модели: - смеси гауссовских распределений (GMM, Gaussian Mixture Model) [2]; - скрытые марковские модели (HMM, Hidden Markov Model) [3]; - гистограммные модели (Histogram Mo- del) [4]; - алгоритм спектральной кластеризации Ына–Джордана–Вайса (Ng–Jordan–Weiss spectral clustering algorithm) [5]; - алгоритм байесовской адаптации [6]. Считается, что данные модели более подходят для описания поведения, характерного именно для голосового сигнала. Тем не менее, перспективным представляется применение инструментов интеллектуального анализа временных рядов. В настоящей работе для решения данной задачи предлагается использовать подход, основанный на применении улучшенных самоорганизующихся растущих нейронных сетей при кластеризации для характеристик, выделенных из сигнала и уникальных для каждого пользователя. В качестве таких характеристик используются мел-частотные кепстральные коэффициенты. «Кепстр» (cepstrum) [7], результат применения преобразования Фурье к спектру сигнала, часто применяется для задач, связанных с анализом человеческой речи и голоса, так как люди реагируют лишь на частотные изменения звука. Модель пользователя Причины использования мел-частотных кепстральных коэффициентов. Звуковой сигнал – одно из средств взаимодействия человека с окружающей средой и людей между собой. Голос зависит от многих физиологических параметров говорящего и по своей сути является индивидуальной характеристикой каждого человека. Тем не менее, это не постоянная характеристика, голос изменяется в течение жизни человека, на него влияют состояние здоровья и эмоции.
Также в процессе эволюции звуки в более низком частотном диапазоне содержат больше полезной информации, чем находящиеся в более высоком частотном диапазоне. С учетом этих особенностей человеческого слуха были разработаны мел-частотные кепстральные коэффициенты («мел» – сокращение английского слова «melody» (мелодия)) [9]. С помощью данных коэффициентов тщательнее анализируется информация, получаемая из низкочастотного диапазона, а влияние высокочастотных составляющих, обычно содержащих посторонний шум, на результат распознавания уменьшается. Вся голосовая запись разделяется на небольшие интервалы длительностью ~10–30 мс (время квазистационарности сигнала), называемые фреймами. Для каждого фрейма отдельно рассчитывается набор мел-частотных кепстральных коэффициентов, который в дальнейшем будет использоваться для кластеризации. Вычисление мел-частотных кепстральных коэффициентов. Алгоритм вычисления мел-частотных кепстральных коэффициентов можно разбить на следующие этапы [10, 11]: – разбиение сигнала на фреймы; – применение весовой функции (окна) к _ каждому фрейму; – применение преобразования Фурье; – использование мел-частотного фильтра; – вычисление кепстра. Разбиение сигнала на фреймы. Звуковой сигнал в общем случае не является стационарным, то есть его амплитуда и спектр изменяются во времени, что приводит к невозможности применения многих техник анализа. Но отдельно взятый короткий интервал порядка 10–30 мс можно считать стационарным. Часто применяют следующую методику деления сигнала на фреймы: сигнал разделяется на интервалы длиной N мс следующим образом: начало первого фрейма совпадает с началом записи, второй фрейм начинается через M мс интервалов (M < N), соответственно, он на N–M мс перекрывает первый фрейм. На рисунке 1 показан случай для N = 20 мс и М = 16 мс. Несмотря на стационарность, такое представление сигнала не позволяет использовать преобразование Фурье. Если частоты гармоник (частотных составляющих) сигнала не совпадают с базисными частотами преобразования Фурье, в спектре могут возникать «лишние» гармоники, которые будут лишь «зашумлять» полученное представление. Данный эффект носит название «размытие спектра» или «спектральная утечка». Применение весовой функции (окна). Одним из возможных вариантов решения возникшей проблемы является применение к сигналу весовой функции специального вида: w(n), 0 £ n £ N–1. Результат применения весовой функции к каждому фрейму выглядит следующим образом: y(n) = x(n)×w(n), 0 £ n £ N–1, где x(n) – значение временного ряда в точке n; y(n) – взвешенное значение временного ряда в точке n (рис. 2a). Наиболее предпочтительно применение «мягких» весовых функций, которые сводят значения на границах фрейма к нулю. Эта операция называется «сглаживанием». Наиболее часто используемой является весовая функция Хэмминга, которую можно представить следующей формулой [10, 11]:
Преобразование Фурье, примененное к «взвешенному» временному ряду, дает более четкий, содержащий меньше «лишних» гармоник спектр (рис. 2б). Преобразование Фурье. На следующем этапе необходимо применить преобразование Фурье, которое переведет сигнал из временного пространства в частотное. На практике чаще всего применяется быстрое преобразование Фурье, имеющее следующий вид [8]:
где yk – взвешенное значение временного ряда в точке k; Yn – комплексная амплитуда n-й гармоники сигнала, представляемого временным рядом. Результатом данного этапа является спектр сигнала. Использование мел-частотного фильтра. На данном этапе к спектру сигнала применяется фильтр специального вида. Каждому значению частоты, полученному на предыдущем шаге, ставится в соответствие значение на мел-частотной шкале. Значения данной шкалы для частот ниже 1 000 Гц точно соответствуют спектру сигнала, полученному при преобразовании Фурье, частоты выше 1 000 Гц логарифмируются. В результате получается модифицированный энергетический спектр сигнала mel(f) для каждой гармоники частоты f, для вычисления которого используется следующая приближенная формула [10]:
К данному спектру применяется фильтр специального вида, ставящий в соответствие каждой частоте определенный набор мел-коэффициентов
где Акустические векторы. Данный алгоритм применяется к каждому фрейму, в результате чего последнему соответствует набор мел-коэффициентов, который используется в большинстве работ как модель пользователя для кластеризации и называется акустическим вектором. Но изменение мел-коэффициентов также содержит определенную информацию о пользователе. Основное отличие данной работы от предыдущих – расширение акустического вектора путем учета динамики изменения мел-коэффициентов δi, которая выражается разностью мел-частотных кепстральных коэффициентов данного фрейма и предыдущего: При данном подходе первый фрейм не может использоваться для кластеризации, так как изменение мел-частотных кепстральных коэффициентов будет нулевым. А L – количество элементов акустического вектора x – увеличивается вдвое:
Использование улучшенных самоорганизующихся растущих нейронных сетей для кластеризации Задача кластеризации пользователя по акустическому вектору относится к классу задач распознавания по шаблону. Существует множество подходов для решения задачи кластеризации данных (иерархические, графовые, нечеткие методы и т.д.) [11]. В последнее время все больший интерес исследователей вызывает применение нейронных сетей при кластеризации. В частности, часто используют нейронные сети Кохоннена [13, 14] из-за высокой скорости кластеризации. Данный метод основан на проецировании многомерного пространства в двухмерное с переопределенной структурой. Однако при данном подходе возникают дефекты проецирования, анализ которых является сложной задачей. В силу статической структуры сети невозможно добавление кластеров для новых пользователей, начинающих использовать систему. Также невозможно интерактивное обучение сети для новых данных на этапе ее функционирования, переобучение же может привести к потере результатов предыдущего обучения. Для снятия данных ограничений были разработаны самоорганизующиеся растущие нейронные сети (self-organizing incremental neural network, SOINN) [15, 16]. С помощью этих сетей можно осуществлять кластеризацию данных без априорного знания их топологии, модель также поддерживает обучение без конечной цели на протяжении всего периода функционирования сети (lifetime learning), что позволяет не ограничивать максимальное количество кластеров. SOINN представляют собой нейронную сеть с двумя слоями. Первый слой используется для определения топологической структуры кластеров, второй – для определения числа кластеров. Сначала обучается первый слой, а затем, используя выходные данные первого слоя в качестве входных, обучается второй слой сети. Исследователь должен самостоятельно определить момент, когда необходимо начать обучение второго слоя, а также вычислить порог T для каждого слоя сети. При отсутствии априорных знаний о структуре данных порог для первого слоя подбирается адаптивно. Основной идеей алгоритма обучения сети является построение вероятностной модели входных данных. Исходя из предположения, что кластеры образуют области высокой плотности вероятности, необходимо построить граф, наиболее точно описывающий такие области и их взаимное расположение в пространстве. Вершины графа лежат в областях локального максимума вероятности, а его ребра соединяют вершины, относящиеся к одному кластеру. Большое количество параметров сети и неопределенность в выборе момента начала обучения второго слоя затрудняют применение сетей SOINN на практике. К тому же при любых изменениях в первом слое необходимо полностью переобучать второй слой, что делает в общем случае невозможным постоянное интерактивное обучение сети в процессе функционирования. Для решения озвученных проблем были разработаны улучшенные самоорганизующиеся растущие нейронные сети (enhanced self-organizing neural network, ESOINN) [17]. В настоящей работе данный вид сетей применяется к задаче кластеризации пользователя по голосу. Основным отли- чием данного подхода является использование однослойной нейронной сети, что уменьшает число настраиваемых параметров и снимает необходимость определения момента перехода от обучения первого слоя ко второму вручную. Алгоритм обучения сети ESOINN выглядит следующим образом [17]. 1. Инициализировать набор узлов A двумя узлами с векторами признаков, взятыми случайным образом из области допустимых значений. Инициализировать набор связей (ребер графа) C(CÎA´A) пустым множеством. 2. Подать на вход акустический вектор xÎℝn, где n – размерность акустического вектора. 3. Найти ближайший узел a1 (нейрон-победитель) и второй ближайший узел a2 (второй нейрон-победитель) по формулам:
где xÎℝn – вектор признаков входного объекта; WaÎℝn – вектор признаков вершины (нейрона) a. 4. Если расстояния между вектором признаков входного объекта и нейроном a1 или a2 больше некоторого заданного порога
5. Увеличить временную метку всех ребер, исходящих из a1, на 1. Считаем, что каждому ребру в графе соответствует временная метка, обозначающая время последнего использования этого ребра. 6. Используя алгоритм Conn, определить, нужна ли связь между a1 и a2: – если связь необходима, создать ребро a1®a2 (если его не существует) и установить его временную метку равной 0; – если ребро существует, удалить его. 7. Увеличить число побед нейрона a1 по формуле 8. Обновить плотность вероятности для нейрона-победителя по формуле
где hiÎℝ – плотность вероятности в i-й вершине графа (нейроне); 9. Адаптировать векторы признаков победителя и его топологических соседей с весовыми коэффициентами e1(t) и e2(t) по следующим формулам: 10. Найти и удалить те ребра, временная метка которых превышает некоторое пороговое значение для сети 11. Если число входных сигналов, генерируемых до этого шага, кратно некоторому параметру l, необходимо: а) обновить метки кластеров для всех узлов, используя алгоритм Part (Partition); б) удалить узлы, являющиеся шумом: – для всех узлов a из A: если узел имеет не менее двух соседей и плотность вероятности для данного узла – для всех узлов a из A: если узел имеет одного соседа и – для всех узлов a из A: если узел не имеет соседей, то удалить этот узел. 12. Если процесс обучения закончен, то классифицировать узлы различных классов, используя алгоритм выделения связных компонент графа. Иначе – перейти к шагу 2. Алгоритм Conn (Connection). Построение связи между вершинами. Соединим два узла в том случае, если – – они принадлежат к одному кластеру; – они принадлежат к различным кластерам, и при этом выполняется условие на слияние этих кластеров (алгоритм Part). Иначе не соединяем эти узлы. Если между ними уже существует связь, удаляем ее. Использование условия из алгоритма Part позволяет успешно проводить кластеризацию близко расположенных классов. Алгоритм Part. Разбиение сложного кластера. 1. Назовем узел (нейрон) вершиной кластера, если он имеет максимальную плотность вероятности в окрестности. Необходимо найти все такие вершины в сложном кластере и присвоить им различные метки. 2. Отнесем остальные узлы к тем же кластерам, что и у ближайших к ним вершин. 3. Узлы лежат в области перекрытия классов, если они принадлежат разным классам и имеют общее ребро. На практике такой способ разделения класса на подклассы приводит к тому, что при наличии шумов большой класс может быть ложно классифицирован как несколько небольших классов. Поэтому, прежде чем разделить классы, необходимо сгладить их. Предположим, что у нас есть два несглаженных кластера (подкласса) A и B, плотность вершины подкласса A равна Amax, а у подкласса B равна Bmax. Объединим A и B в один подкласс в том случае, если выполняются следующие условия:
Здесь первый и второй победители лежат в области перекрытия подклассов A и B. Параметр a вычисляется следующим образом:
где meanY – средняя плотность узлов в подклас- се Y. После этого удалим все ребра, соединяющие вершины различных классов. Таким образом мы разделяем композитный класс на подклассы, не перекрывающие друг друга. Процесс кластеризации входит в процесс обучения сети на всех этапах, за исключением шага 1. Результат обучения сети. После обучения нейронная сеть будет представлять собой граф, вершинами которого являются нейроны-победители (центры кластеров центроиды). Центроиды, соединенные ребром, ассоциированы с одним пользователем. Проекцию результата обучения сети в двумерном пространстве можно проиллюстрировать рисунком (рис. 3). В данном примере центроиды, соответствующие одному пользователю, а также ассоциированные с ними акустические векторы выделены соответствующей формой (круг или треугольник). Практическая реализация данного метода Для вычисления мел-частотных кепстральных коэффициентов используются средства свободно распространяемого фреймворка Sphinx 4, разработанного в университете Карнеги-Меллон [18]. Данный комплекс реализует множество функций, необходимых для распознавания пользователей по голосу, и обладает простым интерфейсом. Система реализована в виде библиотеки C++, так как данный язык обладает кроссплатформенностью и высокой производительностью вычислений. В настоящее время ведется исследование возможности дополнения программного комплекса блоком сегментации записи, если на одной записи присутствуют голоса двух или более пользователей. В заключение отметим, что данная работа рассматривает кластеризацию пользователей по голосу. В качестве характеристик пользователя предлагается использовать расширенный акустический вектор каждого фрейма голосовой записи, состоящий из мел-частотных кепстральных коэффициентов, а также приближений их первых производных. В качестве алгоритма кластеризации используются улучшенные самоорганизующиеся растущие нейронные сети, так как их использование позволяет производить кластеризацию без априорных знаний структуры данных, а также осуществлять обучение сети на всем этапе ее функционирования без конечной цели. Предложенный метод учитывает дополнительные особенности голосовых характеристик каждого пользователя, в частности скорость изменения частот голоса. Литература 1. NIST RTE. URL: http://nist.gov/itl/iad/mig/rt.cfm (дата обращения: 26.03.2015). 2. Han K.J., Narayanan S.S. Agglomerative Hierarchical Speaker Clustering using Incremental Gaussian Mixture Cluster Modeling. Proc. of InterSpeech, 2008, pp. 20–23. 3. Ajmera J., Wooters C. A Robust Speaker Clustering Algorithm. IEEE Workshop on Automatic Speech Recognition and Understanding, 2003, pp. 411–416. 4. Rodriguez L.J, Torres M.I. A Speaker Clustering Algorithm for Fast Speaker Adaptation in Continuous Speech Recognition. Text, Speech and Dialogue: Lecture Notes in Computer Science, 2004, vol. 3206, pp. 433–440. 5. Ning H., Liu M., Tang H., Huang Th. A Spectral Clustering Approach to Speaker Diarization. Proc. ICSLP, 2006, pp. 2178–2181. 6. Faltlhauser R., Ruske G. Robust Speaker Clustering in Eigenspace. IEEE Workshop on Automatic Speech Recognition and Understanding, 2001, pp. 57–60 7. Bogert B.P., Healy M.J.R., Tukey J.W. The Quefrency Alanysis of Time Series for Echoes: Cepstrum, Pseudo Autocovariance, Cross-Cepstrum and Saphe Cracking. Proc. of the Symposium on Time Series Analysis (M. Rosenblatt, Ed). NY, Wiley, 1963, Chapter 15, pp. 209–243. 8. Cooley J.W., Tukey J.W. An Algorithm for the Machine Calculation of Complex Fourier Series. Mathematics of Computation, 1965, pp. 297–301. 9. Vyas G., Kumari B. Speaker Recognition System Based on MFCC and DCT. Intern. Journ. of Engineering and Advanced Technology (IJEAT), 2013, vol. 2, iss. 5. 10. Molau S., Pitz M., Schlüter R., Ney H. Computing mel-frequency cepstral coefficients on the power spectrum. IEEE Intern. Conf. on Accoustics, Speech, and Signal Processing, 2001, vol. 1, pp. 73–76. 11. Вагин В.Н., Головина Е.Ю., Загорянская А.А., Фоми- на М.В. Достоверный и правдоподобный вывод в интеллектуальных системах. 2-е изд. М.: Физматлит, 2008. 712 с. 12. Chougala M., Unnibhavi A.H. Comparison of conventional MFCC with new Efficient MFCC Extraction Method in Speech Recognition. IPADJ Intern. Journ. of Computer Science (IIJCS), 2015, vol. 3, iss. 4, pp. 7–12. 13. Kumar Ch.S., Rao P.M. Design of an Automatic Speaker Recognition System using MFCC, Vector Quantization and LBG Algorithm. Intern. Journ. on Coputer Science and Engineering (IJCSE), 2011, vol. 3, iss. 8, pp. 2942–2954. 14. Mori K., Nakagawa S. Speaker change detection and speaker clustering using VQ distortion for broadcast news speech recognition. Acoustics, Speech, and Signal Processing. Proc. (ICASSP '01). IEEE Intern. Conf., 2001, vol. 1, pp. 413–416. 15. Furao S., Hasegawa O. An incremental network for on-line unsupervised classification and topology learning. Neural Networks, 2006, vol. 19, iss. 1, pp. 90–106. 16. Tang Z., Furao S., Jinxi Z. Speaker recognition based on SOINN and incremental learning Gaussian mixture model. Neural Networks, 2013, pp. 1–6. 17. Furao S., Ogura T., Hasegawa O. An enhanced self-organizing incremental neural network for online unsupervised learning. Neural Networks, 2007, vol. 20, iss. 8, pp. 893–903. 18. Walker W., Lamere P., Kwok P., Raj B., Singh R., Gouvea E., Wolf P., Woelfel J. Sphinx-4: A flexible open source framework for speech recognition. Technical Report, 2004. |
| Permanent link: http://swsys.ru/index.php?id=4041&lang=en&page=article |
Print version Full issue in PDF (8.21Mb) Download the cover in PDF (1.09Мб) |
| The article was published in issue no. № 3, 2015 [ pp. 136-142 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Оптимальная энтропийная кластеризация в информационных системах
- Принятие проектных решений на основе анализа нечетких тенденций временных рядов
- Визуализация и анализ баз знаний интеллектуальных систем
- Разработка теоретических основ классификации и кластеризации нечетких признаков на основе теории категорий
- Аспекты применения предметно-ориентированного подхода к проектированию сложных программных систем
Back to the list of articles
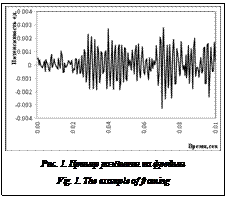 Современные средства записи позволяют представить звуковой сигнал в виде временного ряда, показывающего изменение интенсивности звука во времени. Однако такое представление затрудняет анализ, так как содержит большое количество информационного шума. Спектр сигнала, его представление в частотном пространстве более информативны для анализа, чем сигнал сам по себе. Для вычисления спектра часто используется быстрое преобразование Фурье, алгоритм которого достаточно прост для реализации и имеет меньшую сложность O(Nlog2N), чем классический алгоритм дискретного преобразования Фурье O(N2) [8].
Современные средства записи позволяют представить звуковой сигнал в виде временного ряда, показывающего изменение интенсивности звука во времени. Однако такое представление затрудняет анализ, так как содержит большое количество информационного шума. Спектр сигнала, его представление в частотном пространстве более информативны для анализа, чем сигнал сам по себе. Для вычисления спектра часто используется быстрое преобразование Фурье, алгоритм которого достаточно прост для реализации и имеет меньшую сложность O(Nlog2N), чем классический алгоритм дискретного преобразования Фурье O(N2) [8]. .
. ,
, .
. , 1, ..., K, где K – количество мел-коэффициентов (на практике часто выбирают значение от 12 до 24).
, 1, ..., K, где K – количество мел-коэффициентов (на практике часто выбирают значение от 12 до 24).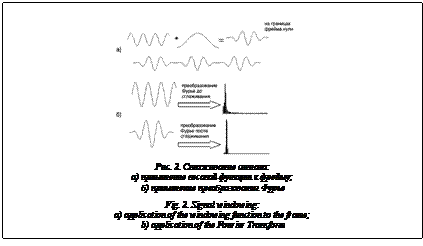 Использование мел-частотного фильтра. На предыдущем шаге алгоритма полученные коэффициенты
Использование мел-частотного фильтра. На предыдущем шаге алгоритма полученные коэффициенты 
 – полученные мел-частотные кепстральные коэффициенты.
– полученные мел-частотные кепстральные коэффициенты. .
.
 ,
, ,
, или
или  то он порождает новый узел: добавление нового узла и переход на шаг 2.
то он порождает новый узел: добавление нового узла и переход на шаг 2. вычисляются по следующим формулам:
вычисляются по следующим формулам:  , если нейрон имеет соседей,
, если нейрон имеет соседей,  , если нейрон не имеет соседей, Ni
, если нейрон не имеет соседей, Ni  – количество узлов соседей нейрона i; N – общее количество нейронов в слое.
– количество узлов соседей нейрона i; N – общее количество нейронов в слое. , где MiÎℤ – число побед нейрона i.
, где MiÎℤ – число побед нейрона i. ,
, – среднее расстояние между узлами внутри кластера, к которому принадлежит победитель:
– среднее расстояние между узлами внутри кластера, к которому принадлежит победитель:  , m – количество узлов (нейронов) внутри кластера.
, m – количество узлов (нейронов) внутри кластера. ,
,  для каждого соседа i; коэффициенты e1(t) и e2(t) вычисляются по формулам [15]:
для каждого соседа i; коэффициенты e1(t) и e2(t) вычисляются по формулам [15]:  ,
,  .
. .
. , то удалить этот узел;
, то удалить этот узел; , то удалить этот узел;
, то удалить этот узел;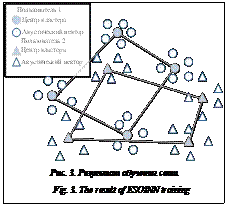 хотя бы один из них является новым узлом и еще не определено, к какому кластеру он относится;
хотя бы один из них является новым узлом и еще не определено, к какому кластеру он относится; или
или .
.
