К важнейшим задачам при моделировании динамики трехмерных виртуальных объектов (тел) относятся определение и обработка их столкновений (коллизий) [1]. Определение коллизий объектов произвольных форм является вычислительно сложной задачей [2], поэтому широкое распространение получил метод определения коллизий, при котором каждый динамический объект окружается (аппроксимируется) одним или несколькими геометрическими контейнерами (параллелепипедами, сферами и т.д.) [3]. Тогда моделирование столкновения двух тел заключается в определении параметров (точки, глубины и нормали) коллизии аппроксимирующих контейнеров двух объектов и в задании реакции тел на это столкновение.
Алгоритмы определения коллизий делятся на два вида: априорные и апостериорные [4]. Априорные алгоритмы предсказывают столкновения тел, апостериорные определяют коллизию объектов уже по факту их столкновения. В общем случае априорные алгоритмы обладают большей точностью вычисления информации о коллизии, но их существенным недостатком является большая вычислительная сложность, связанная с большим объемом входных данных (положение и ориентация объектов, а также их физические параметры: скорость, сила, моменты и т.д.). В связи с этим системы динамики, основанные на априорных определениях коллизий, работают в режиме реального времени (не менее 25 шагов моделирования в секунду) лишь для небольшого числа виртуальных объектов. Для апостериорных алгоритмов опреде- ления коллизий входной объем данных сводится только к положению и ориентации объектов.
В настоящей работе рассматриваются методы апостериорного определения коллизий двух сфер и сферы с прямоугольным параллелепипедом (боксом). Коллизии боксов между собой рассмотрены в [5].
Понятие коллизии
В данной работе будут использоваться правосторонние системы координат. Для каждого аппроксимирующего контейнера задается матрица перехода из его локальной системы координат в мировую [6]. Первые три столбца этой матрицы задают ориентацию тела, а четвертый – положение начала локальной системы координат тела в мировой системе координат.
Обозначим радиус сферы через r, а начало ее локальной системы координат расположим в центре сферы.
Размеры бокса задаются величинами l (половина длины), w (половина ширины) и h (высота). Начало локальной системы координат расположим в центре нижней грани бокса так, что ось x направлена параллельно ребру бокса, задающему его длину, ось y – ширину, а ось z – высоту.
Под определением коллизии пары аппроксимирующих контейнеров понимается определение факта их пересечения и, в случае его наличия, вычисление точки коллизии, нормали расталкивания и глубины коллизии.
Точка, нормаль и глубина коллизии. В качестве первого объекта коллизии всегда будем рассматривать сферу, а вторым объектом будет либо сфера, либо бокс. Определим точку коллизии как точку поверхности второго объекта, наиболее близкую к центру первого. Под нормалью коллизии будем подразумевать единичный вектор, направленный вдоль прямой, проходящей через точку контакта и центр первого объекта, и указывающий направление расталкивания для первого объекта. Глубина коллизии – это расстояние, на которое точка коллизии проникла в первый объект вдоль нормали.
Обозначим через P точку коллизии. Пусть O1 и O2 – положение центров первого и второго объектов в мировой системе координат, а M1 и M2 – соответствующие матрицы перехода. Если вторым объектом является сфера, то ее центр задается четвертым столбцом матрицы M2, если же бокс, то к координате z четвертого столбца надо прибавить h/2 (так как начало системы координат бокса располагается в центре нижнего основания). Тогда нормаль коллизии определим вектором
 , (1)
, (1)
а глубину коллизии величиной
 . (2)
. (2)
Определение коллизии двух сфер

Две сферы пересекаются тогда и только тогда, когда сумма их радиусов больше или равна расстоянию между их центрами (см. рис. 1), то есть |O1 – O2| <= r1 + r2.
Если сферы пересекаются, то точка коллизии лежит на поверхности второй сферы на прямой, соединяющей их центры:  .
.
Проверим совпадение направления нормали (1) с направлением вектора  , который и будет вектором, задающим правильное направление для расталкивания первого объекта. Рассмот- рим два случая: центр O1 находится вне вто- рой сферы (рис. 1а) и центр O1 находится внутри второй сферы (рис. 1б). В первом случае векторы
, который и будет вектором, задающим правильное направление для расталкивания первого объекта. Рассмот- рим два случая: центр O1 находится вне вто- рой сферы (рис. 1а) и центр O1 находится внутри второй сферы (рис. 1б). В первом случае векторы  и
и  направлены в одну сторону, поэто- му
направлены в одну сторону, поэто- му  и, следовательно, вектор
и, следовательно, вектор  также совпадает по направлению с вектором
также совпадает по направлению с вектором  , то есть направление нормали верное. Во втором случае вектор
, то есть направление нормали верное. Во втором случае вектор  направ- лен противоположно вектору
направ- лен противоположно вектору  , поэтому
, поэтому  . Произведение
. Произведение  даст вектор, совпадающий по направлению с вектором
даст вектор, совпадающий по направлению с вектором  , то есть нормаль направлена верно.
, то есть нормаль направлена верно.
Тогда из (2) получаем, что глубина коллизии в первом случае будет  , а во втором –
, а во втором –  .
.
Определение коллизии сферы с прямоугольным параллелепипедом
Для определения коллизии сферы и бокса обозначим через Q точку на поверхности бокса, ближайшую к центру сферы. Рассмотрим всевозможные варианты расположения центра сферы относительно бокса (см. рис. 2).

1. Центр сферы расположен точно над одной из граней бокса. Тогда точкой Q является конец перпендикуляра, опущенного из центра сферы к этой грани (точка Q1 на рисунке 2).
2. Центр сферы расположен по диагонали от одного из ребер бокса, то есть вне двух соседних граней, содержащих это ребро. Тогда точкой Q является конец перпендикуляра, опущенного из центра сферы к этому ребру бокса (точка Q2 на рисунке 2).
3. Центр сферы расположен по диагонали от одной из вершин бокса, то есть вне трех соседних граней, содержащих эту вершину. Тогда точкой Q будет эта вершина бокса (точка Q3 на рисунке 2).
4. Центр сферы лежит внутри бокса. Тогда точкой Q является конец перпендикуляра, опущенного из центра сферы к ближайшей грани бокса (точка Q4 на рисунке 2).
Обозначим через E1 систему координат сферы, а через E2 систему координат бокса. Рассмотрим достаточно быстрый алгоритм, позволяющий определить положение центра сферы относительно бокса. Причем, если центр сферы лежит вне бокса, алгоритм сразу вычисляет точку Q. Суть алгоритма – перевод вектора  из мировой системы координат в систему E2 и его покомпонентное сравнение с полуразмерами бокса. Обозначим совокупность координат вектора
из мировой системы координат в систему E2 и его покомпонентное сравнение с полуразмерами бокса. Обозначим совокупность координат вектора  в системе координат E2 через
в системе координат E2 через 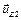 . Получим
. Получим  .
.
Тогда с использованием компонент x, y и z вектора 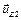 алгоритм будет следующим.
алгоритм будет следующим.
Если  , то
, то
 ,
,
иначе, если 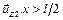 , то
, то
 .
.
Если  , то
, то
 ,
,
иначе, если  , то
, то
 .
.
Если  , то
, то
 ,
,
иначе, если  , то
, то
 .
.
Если выполняется хотя бы одно из данных условий, значит, центр сферы лежит вне бокса. Тогда точка Q в системе координат E2 будет  , а в мировой
, а в мировой 
 .
.
Если не выполнилось ни одно из условий, значит, центр сферы лежит внутри бокса. Рассмотрим отдельно оба случая.
Центр сферы лежит вне бокса. Сфера и бокс пересекаются тогда и только тогда, когда радиус сферы больше расстояния от ее центра О1 до точки Q, то есть |O1 – Q| £ r1.
Если сфера и бокс пересекаются, точка кол- лизии Р будет совпадать с Q. Ясно, что соответствующие координаты векторов  и
и  в системе E2 имеют одинаковые знаки, поэтому
в системе E2 имеют одинаковые знаки, поэтому  . Тогда из (1) следует, что
. Тогда из (1) следует, что  совпадет по направлению с
совпадет по направлению с  (то есть будет соответствовать направлению расталкивания сферы), а из (2) получаем
(то есть будет соответствовать направлению расталкивания сферы), а из (2) получаем 
Центр сферы лежит внутри бокса. В этом случае вектор  будет соединять центр бокса с центром сферы (см. рис. 3).
будет соединять центр бокса с центром сферы (см. рис. 3).

Вычислим направление  и расстояние min от центра сферы до ближайшей грани бокса:
и расстояние min от центра сферы до ближайшей грани бокса:
 ,
, .
.
Если  , то
, то
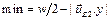 ,
,  .
.
Если  , то
, то
 ,
,
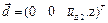 .
.
Тогда точка коллизии  .
.
Проверим, что направление нормали (1) будет противоположно направлению вектора  , то есть будет правильным для расталкивания первого объекта. Ясно, что косинус угла между векторами
, то есть будет правильным для расталкивания первого объекта. Ясно, что косинус угла между векторами  и
и  отрицательный, то есть
отрицательный, то есть  . Следовательно, направление нормали будет противоположно направлению
. Следовательно, направление нормали будет противоположно направлению  . Тогда из (2) получаем, что в этом случае глубина коллизии
. Тогда из (2) получаем, что в этом случае глубина коллизии  .
.
 В заключение отметим, что рассмотренные алгоритмы определения коллизий двух сфер между собой и сферы с прямоугольным параллелепипедом позволяют вычислять информацию о коллизиях с небольшой вычислительной сложностью. Вместе с обработкой коллизий, описанной в [7], это позволяет моделировать динамику в режиме реального времени большого (вплоть до нескольких тысяч) количества виртуальных объектов. Данные алгоритмы были реализованы в рамках динамической библиотеки, входящей в состав существующей системы трехмерного моделирования виртуальных объектов. За счет наличия в этой системе модуля визуализации [8, 9] реализованные алгоритмы были проверены на наборе тестовых сцен, имитирующих различные ситуации при столкновении виртуальных объектов. Особое внимание было уделено сложной в плане моделирования динамики ситуации покоя множества тел друг на друге (см. рис. 4). Сложность такой ситуации при моделировании динамики в том, что на тела постоянно действует сила тяжести. Таким образом, тела постоянно стремятся проникать друг в друга, а подсистема определения и обработки коллизий этому противодействует. До тех пор, пока в этой подсистеме получаемые расчеты по обработке коллизий не полностью удовлетворяют условию покоя всех тел одновременно, объекты совершают небольшие движения вверх-вниз (подрагивают).
В заключение отметим, что рассмотренные алгоритмы определения коллизий двух сфер между собой и сферы с прямоугольным параллелепипедом позволяют вычислять информацию о коллизиях с небольшой вычислительной сложностью. Вместе с обработкой коллизий, описанной в [7], это позволяет моделировать динамику в режиме реального времени большого (вплоть до нескольких тысяч) количества виртуальных объектов. Данные алгоритмы были реализованы в рамках динамической библиотеки, входящей в состав существующей системы трехмерного моделирования виртуальных объектов. За счет наличия в этой системе модуля визуализации [8, 9] реализованные алгоритмы были проверены на наборе тестовых сцен, имитирующих различные ситуации при столкновении виртуальных объектов. Особое внимание было уделено сложной в плане моделирования динамики ситуации покоя множества тел друг на друге (см. рис. 4). Сложность такой ситуации при моделировании динамики в том, что на тела постоянно действует сила тяжести. Таким образом, тела постоянно стремятся проникать друг в друга, а подсистема определения и обработки коллизий этому противодействует. До тех пор, пока в этой подсистеме получаемые расчеты по обработке коллизий не полностью удовлетворяют условию покоя всех тел одновременно, объекты совершают небольшие движения вверх-вниз (подрагивают).
Система динамики в примере покоя объектов друг на друге показала убедительные результаты времени расчетов. На просчет одного шага моделирования при наличии незначительного дрожания объектов уходит не более 3 мс. В течение небольшого количества шагов моделирования объекты перестают дрожать и переходят в статическое положение, при котором определение и обработка их коллизий прекращаются и на просчет одного шага моделирования уходит менее 1 мс.
Литература
1. Moore M., Wilhelms J. Collision Detection and Response for Computer Animation. Computer Graphics, 1998, vol. 22, no. 4, pp. 289–298; URL: http://www.cs.princeton.edu/courses/archive/ spring01/cs598b/papers/moore88.pdf (дата обращения: 10.07.2015).
2. Ming C. Lin, Gottschalk S. Collision detection between geometric models: a survey. Proc. of IMA conference on mathematics of surfaces. 1998, vol. 1, pp. 602–608; URL: https://users.soe.ucsc.edu/~pang/161/w06/notes/cms98.pdf (дата обращения: 10.07.2015).
3. Bounding volume. URL: https://en.wikipedia.org/wiki/Bounding_volume (дата обращения: 10.07.2015).
4. Ericson C. Real-Time Collision Detection. CRC Press, 2004, 594 p.; URL: https://books.google.ru/books?id=WGpL6 Sk9qNAC (дата обращения: 10.07.2015).
5. Михайлюк М.В., Трушин А.М. Расчет коллизий прямоугольных параллелепипедов в задачах динамики // Труды НИИСИ РАН. Т. 2. № 2. Обработка изображений, моделирование и визуализация: теоретические и прикладные аспекты. 2012. С. 51–59.
6. Transformation matrix. URL: https://en.wikipedia.org/wiki/Transformation_matrix (дата обращения: 10.07.2015).
7. Трушин А.М. Обработка коллизий виртуальных объектов с помощью метода последовательных импульсов // Труды НИИСИ РАН. Т. 4. № 2. Математическое и компьютерное моделирование сложных систем: теоретические и прикладные аспекты. 2014. С. 95–105.
8. Михайлюк М.В., Торгашев М.А. Система «GLVIEW» визуализации для моделирующих комплексов и систем виртуальной реальности // Вестн. РАЕН. 2011. № 2. C. 20–28.
9. Михайлюк М.В., Торгашев М.А. Визуализация динамики объектов управления в реальном времени // Научная визуализация. 2014. Т. 6. № 5. C. 69–80; URL: http://sv-journal.org/2014-5/index2139.html?lang=ru (дата обращения: 10.07.2015).
 , (1)
, (1) . (2)
. (2)
 .
. , который и будет вектором, задающим правильное направление для расталкивания первого объекта. Рассмот- рим два случая: центр O1 находится вне вто- рой сферы (рис. 1а) и центр O1 находится внутри второй сферы (рис. 1б). В первом случае векторы
, который и будет вектором, задающим правильное направление для расталкивания первого объекта. Рассмот- рим два случая: центр O1 находится вне вто- рой сферы (рис. 1а) и центр O1 находится внутри второй сферы (рис. 1б). В первом случае векторы  и
и  и, следовательно, вектор
и, следовательно, вектор  также совпадает по направлению с вектором
также совпадает по направлению с вектором  . Произведение
. Произведение  , а во втором –
, а во втором –  .
.
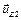 . Получим
. Получим  .
. , то
, то ,
,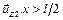 , то
, то .
. , то
, то ,
, , то
, то .
. , то
, то ,
, , то
, то .
. , а в мировой
, а в мировой 
 .
. в системе E2 имеют одинаковые знаки, поэтому
в системе E2 имеют одинаковые знаки, поэтому  совпадет по направлению с
совпадет по направлению с 
 будет соединять центр бокса с центром сферы (см. рис. 3).
будет соединять центр бокса с центром сферы (см. рис. 3).
 и расстояние min от центра сферы до ближайшей грани бокса:
и расстояние min от центра сферы до ближайшей грани бокса: ,
, .
. , то
, то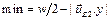 ,
,  .
. , то
, то ,
, .
. .
.
