В настоящее время в России количество разработок новых, оригинальных составов лекарственных средств невелико. Преимущественно это дженерики – лекарственные препараты, являющиеся терапевтическим эквивалентом брендового препарата и выпускающиеся только после истечения срока действия патента на оригинальный препарат [1]. Дженерики позволяют обеспечить замещение оригинальных лекарственных средств за счет более низкой стоимости по сравнению с оригинальными препаратами. При разработке составов дженериков, а также оригинальных препаратов необходимы многократные эксперименты по растворению различных составов веществ, что является ресурсоемким с точки зрения времени и денежных средств [2]. Таким образом, моделирование процесса растворения, позволяющего предсказать кинетику растворения твердого тела и подобрать оптимальный состав лекарственного средства, является актуальной задачей.
Ранее была разработана модель процесса растворения на основе клеточных автоматов [3]. Однако клетки в ней имеют фиксированный размер, что накладывает некоторые ограничения на модель: во-первых, переход вещества из твердого состояния в жидкое происходит за одну итерацию, а во-вторых, невозможен учет реального изменения размеров твердого тела в процессе растворения. Данные ограничения оказывают влияние на точность расчетов.
 На стадии разработки составов дженериков, а также оригинальных лекарственных средств важным этапом является проверка соответствия кинетики растворения активного вещества кинетике растворения, заданной в фармакопейной статье либо научно-исследовательским отделом разработок лекарственных средств. На рисунке 1 приведен разработанный алгоритм модификации состава твердых лекарственных форм. Первым этапом алгоритма является выбор активного вещества и вспомогательных компонентов, входящих в состав лекарственного средства. С целью быстрого доступа к актуальной информации о вспомогательных веществах, их свойствах, производителях и поставщиках была разработана БД вспомогательных веществ [4].
На стадии разработки составов дженериков, а также оригинальных лекарственных средств важным этапом является проверка соответствия кинетики растворения активного вещества кинетике растворения, заданной в фармакопейной статье либо научно-исследовательским отделом разработок лекарственных средств. На рисунке 1 приведен разработанный алгоритм модификации состава твердых лекарственных форм. Первым этапом алгоритма является выбор активного вещества и вспомогательных компонентов, входящих в состав лекарственного средства. С целью быстрого доступа к актуальной информации о вспомогательных веществах, их свойствах, производителях и поставщиках была разработана БД вспомогательных веществ [4].
В зависимости от желаемых свойств конечной лекарственной формы выбирается технология ее получения [5, 6]. Следующим этапом алгоритма является расчет кинетики растворения активного вещества на основе модели растворения [7, 8]. Далее производится проверка соответствия рассчитанной кинетики растворения заданной кинетике растворения для каждого состава твердой лекарственной формы. Результатом этого этапа является выбор состава, при котором кинетика растворения активного вещества воспроизводит заданную кинетику растворения или наиболее близка к ней. С целью проверки адекватности рассчитанной кинетики растворения для твердой лекарственной формы выбранного состава осуществляются экспериментальные исследования. В случае их неудовлетворительного результата состав твердой лекарственной формы корректируется.
Для предсказания кинетики растворения активных веществ была разработана клеточно-автоматная модель процесса растворения с изменяющимися размерами клеток [9]. В разработанной модели приняты следующие допущения:
- система представляет собой совокупность клеток;
- поле имеет открытые границы, вещество удаляется из граничных клеток на каждой итерации;
- каждая клетка имеет три характеристики: тип вещества, количество вещества (в молях) и агрегатное состояние (твердое, жидкость);
- расчет процессов ведется итеративно (на каждой итерации процессы растворения и диффузии вещества происходят в один промежуток времени);
- растворяемые вещества не влияют друг на друга.
 Процесс растворения в рамках клеточно-автоматной модели с изменяющимися размерами клеток описывается следующим образом. В процессе растворения вещество из клеток с состоянием «твердое» переходит в клетки с состоянием «жидкость», таким образом, количество вещества в клетках изменяется. На этом основании можно считать, что изменяются объем клеток при неизменной плотности и, следовательно, их размер. Во всех парах клеток «жидкость–твердое» происходит смещение их границы в сторону клетки с состоянием «твердое», то есть в клетке с состоянием «твердое» количество вещества уменьшается, а в клетках с со- стоянием «жидкость» количество растворяемого вещества увеличивается (рис. 2).
Процесс растворения в рамках клеточно-автоматной модели с изменяющимися размерами клеток описывается следующим образом. В процессе растворения вещество из клеток с состоянием «твердое» переходит в клетки с состоянием «жидкость», таким образом, количество вещества в клетках изменяется. На этом основании можно считать, что изменяются объем клеток при неизменной плотности и, следовательно, их размер. Во всех парах клеток «жидкость–твердое» происходит смещение их границы в сторону клетки с состоянием «твердое», то есть в клетке с состоянием «твердое» количество вещества уменьшается, а в клетках с со- стоянием «жидкость» количество растворяемого вещества увеличивается (рис. 2).
В данной клеточно-автоматной модели рассматриваются различные состояния клеток и их соседей. К примеру, если клетка с состоянием «твердое» с четырех сторон окружена клетками с состоянием «жидкость», со всех ее сторон происходит смещение границ клеток «жидкость–твердое», и она уменьшается в размерах. А в случае, когда клетка с состоянием «твердое» окружена тремя клетками с состоянием «жидкость» и клеткой с состоянием «твердое», только с трех сторон граница клеток «жидкость–твердое» будет смещаться в ее сторону.
Модель процесса растворения описывается следующим уравнением:
 (1)
(1)
где D – коэффициент диффузии; F – площадь по- верхности контакта взаимодействующих клеток; Сi, Сj – концентрации в i-й и j-й ячейках.
Клеточно-автоматная модель дополнена уравнением растворения для расчета количества вещества при переходе из твердого состояния в растворенное: 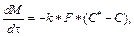 где М – масса твердого вещества; k – коэффициент растворения; F – поверхность растворения; C* – концентрация насыщенного раствора; С – текущая концентрация вещества в растворе. Выражение для расчета коэффициента растворения k в аппаратах с мешалками получено на основе предположения, что реша- ющую роль во внешнем массообмене играет раз- рушение пограничного слоя мелкомасштабными турбулентными пульсациями:
где М – масса твердого вещества; k – коэффициент растворения; F – поверхность растворения; C* – концентрация насыщенного раствора; С – текущая концентрация вещества в растворе. Выражение для расчета коэффициента растворения k в аппаратах с мешалками получено на основе предположения, что реша- ющую роль во внешнем массообмене играет раз- рушение пограничного слоя мелкомасштабными турбулентными пульсациями: 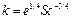 , где e –удельная диссипация механической энергии; Sc – критерий Шмидта.
, где e –удельная диссипация механической энергии; Sc – критерий Шмидта.
На основе данной клеточно-автоматной модели процесса растворения был разработан програм- мный комплекс для расчета кинетики растворения активного вещества. Программный продукт написан на языке С# в среде разработки Microsoft Visual Studio 2013 [10]. Расчет процесса растворения в программном комплексе производится следующим образом. В качестве входных параметров задается линейный размер поля – N клеток и максимальное количество вещества в клетке. Алгоритм расчета процесса растворения состоит в последовательном расчете изменения количества вещества в каждой клетке на каждой итерации. По уравнению модели (1) рассчитываются изменения количества вещества между данной клеткой и каждой из четырех соседних. Затем все четыре изменения количества вещества суммируются и рассчитывается общее изменение количества вещества в данной клетке. Например, для клетки i, j рассчитываются изменения количества вещества: dC(i,j) – (i,j+1), dC(i,j) – (i-1,j), dC(i,j) – (i,j-1) и dC(i,j) – (i+1,j). Общее изменение количества вещества в i, j клетке dCi,j равно сумме dC(i,j) – (i,j+1), dC(i,j) – (i-1,j), dC(i,j) – (i,j-1) и dC(i,j) – (i+1,j).
 На рисунке 3а видим, что алгоритм имеет один недостаток – расчет каждого изменения количества вещества между парой клеток производится дважды на каждой итерации. К примеру, изменение количества вещества dC(i,j) – (i,j+1), вычисляемое для клетки i, j, равно изменению количества вещества dC(i,j+1) – (i,j), вычисляемому для клетки i, j+1. Для устранения данного недостатка был разработан алгоритм, позволяющий избежать повторных вычислений изменений количества вещества.
На рисунке 3а видим, что алгоритм имеет один недостаток – расчет каждого изменения количества вещества между парой клеток производится дважды на каждой итерации. К примеру, изменение количества вещества dC(i,j) – (i,j+1), вычисляемое для клетки i, j, равно изменению количества вещества dC(i,j+1) – (i,j), вычисляемому для клетки i, j+1. Для устранения данного недостатка был разработан алгоритм, позволяющий избежать повторных вычислений изменений количества вещества.
В модифицированном алгоритме производится расчет изменения количества вещества между данной клеткой и только двумя соседними клетками (к примеру, для клетки i, j вычисляются изменения количества вещества dC(i,j) – (i,j+1), dC(i,j) – (i+1,j)), а в качестве значений двух других изменений количества вещества используются вычисленные изменения количества вещества для соседних клеток, только с противоположным знаком (к примеру, для i, j клетки dC(i,j) – (i-1,j)=–dC(i-1,j) – (i,j), а dC(i,j) – (i,j-1)= =dC(i,j-1) – (i,j)). Схема расчета показана на рисунке 3б.
Сокращение вычислений изменений количества вещества в модифицированном алгоритме позволяет ускорить расчет в среднем в 1,5 раза (например, время расчета процесса растворения одной гранулы составляет 3 часа). Процесс расчета заканчивается при выполнении условия растворения твердого тела либо при достижении максимального числа итераций, заданных пользователем.
 В качестве тестовых задач для проверки адекватности разработанной модели было проведено сравнение расчетных данных с экспериментальными на примере растворения различных лекарственных средств. В рамках данной статьи показано использование программного комплекса на примере растворения гранулы сложного состава (рис. 4). Гранула представляет собой распределение включений системы «labrasol–ибупрофен» (на рисунке 4 обозначены зеленым цветом) в смеси растворимых веществ – мальтодекстрин (обозначен синим цветом) и гуммиарабик (обозначен красным цветом). Диаметр одной гранулы – 15 мкм. Рассматривается двумерный случай, когда линейный размер поля клеточного автомата – 300´300 клеток. Размер каждой клетки – 0,1 мкм, соответственно, диаметр гранулы в клеточно-автоматной модели – 150 клеток. Диаметр включений – 1 мкм (в клеточно-автоматной модели – 10 клеток).
В качестве тестовых задач для проверки адекватности разработанной модели было проведено сравнение расчетных данных с экспериментальными на примере растворения различных лекарственных средств. В рамках данной статьи показано использование программного комплекса на примере растворения гранулы сложного состава (рис. 4). Гранула представляет собой распределение включений системы «labrasol–ибупрофен» (на рисунке 4 обозначены зеленым цветом) в смеси растворимых веществ – мальтодекстрин (обозначен синим цветом) и гуммиарабик (обозначен красным цветом). Диаметр одной гранулы – 15 мкм. Рассматривается двумерный случай, когда линейный размер поля клеточного автомата – 300´300 клеток. Размер каждой клетки – 0,1 мкм, соответственно, диаметр гранулы в клеточно-автоматной модели – 150 клеток. Диаметр включений – 1 мкм (в клеточно-автоматной модели – 10 клеток).
Моделирование процесса растворения позволяет построить кинетику высвобождения системы «labrasol–ибупрофен» (масляная фаза) из гранул. На рисунке 5 приведено сравнение экспериментальных и расчетных данных растворения гранул с различными соотношениями мальтодекстрина и гуммиарабика, а также с различной загрузкой масляной фазы (система «labrasol–ибупрофен», МФ). Время растворения составило 360 000 итераций, или 60 минут.
На рисунке 5 точками отмечены экспериментальные значения кинетики растворения ибупрофена, а сплошными линиями – рассчитанные значения.
Визуализация работы программного комплекса в различные моменты времени (0, 5, 30, 60 минут) на примере растворения гранул, содержащих систему «labrasol–ибупрофен», заданного состава представлена на рисунке 6.


Полученные результаты показывают, что расчет отражает общие экспериментально выяв- ленные закономерности: увеличение доли гуммиарабика в гранулах замедляет их растворение, а увеличение содержания масляной фазы ускоряет процесс высвобождения включений системы «labrasol–ибупрофен».
Таким образом, разработанный программный комплекс позволяет моделировать кинетику растворения активных веществ и может быть использован в фармацевтической отрасли для разработки составов дженериков и оригинальных препаратов.
Данный программный комплекс не позволяет учитывать процесс набухания, что накладывает некоторые ограничения на точность расчета, поэтому видимой перспективой является разработка модели набухания. Так как процесс расчета достаточно ресурсоемкий с точки зрения времени, необходимо увеличить производительность, что представляется возможным за счет применения параллельных вычислений с помощью технологии CUDA [11].
Литература
1. Соколов А.В. Оригинальные препараты и дженерики: качество, возможные пути решения проблемы // Медицинские технологии. Оценка и выбор. 2012. № 3 (9). С. 52–56.
2. Илюкевич Г.В., Смирнов В.М., Самолюк Б.Б. Оригинальные лекарственные средства и дженерики: эффективность, безопасность и экономическая целесообразность применения // Лечебное дело. 2013. № 2 (30). С. 24–28.
3. Ivanov S.I., Lovskaya D.D., Menshutina N.V. Cellular automata modeling of dissolution of solid-dosage forms. Computer Aided Chemical Engineering, 2013, vol. 32, pp. 883–888.
4. Меньшутина Н.В., Ершова Е.А., Козлов А.И., Касимо- ва А.О. Вспомогательные вещества для производства твердых лекарственных форм // Программные продукты и системы. 2008. № 3. С. 72–74.
5. Сысуев Б.Б., Плетнева И.В. Современное состояние исследований разработок в области инновационных лекарственных форм и их модификаций // Вестн. Волгоград. гос. мед. ун-та. 2014. № 4 (52). С. 7–12.
6. Leuenberger H. New trends in the production of pharmaceutical granules: batch versus continuous processing. European Journ. of Pharmaceutics and Biopharmaceutics, 2001, no. 52, pp. 289–296.
7. Siepmann J., Siepmann F. Mathematical modeling of drug dissolution. International Journal of Pharmaceutics, 2013, no. 453, pp. 12–24.
8. Bertrand N., Leclair G., Hildgen P. Modeling drug release from bioerodible microspheres using a cellular automaton. Intern. Journ. of Pharmaceutics, 2006, no. 343, pp. 196–207.
9. Ivanov S.I., Tiptsova I.A., Menshutina N.V. Modeling dissolution of solids based on cellular automata with changing sizes of cells. Computer Aided Chemical Engineering, 2015, vol. 37, pp. 605–610.
10. Руководство по программированию на C#. URL: https://msdn.microsoft.com/ru-ru/library/67ef8sbd(v=vs.120).aspx (дата обращения: 12.01.2016).
11. Параллельные вычисления CUDA#. URL: http://www. nvidia.ru/object/cuda-parallel-computing-ru.html (дата обращения: 12.01.2016).


 (1)
(1)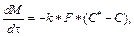 где М – масса твердого вещества; k – коэффициент растворения; F – поверхность растворения; C* – концентрация насыщенного раствора; С – текущая концентрация вещества в растворе. Выражение для расчета коэффициента растворения k в аппаратах с мешалками получено на основе предположения, что реша- ющую роль во внешнем массообмене играет раз- рушение пограничного слоя мелкомасштабными турбулентными пульсациями:
где М – масса твердого вещества; k – коэффициент растворения; F – поверхность растворения; C* – концентрация насыщенного раствора; С – текущая концентрация вещества в растворе. Выражение для расчета коэффициента растворения k в аппаратах с мешалками получено на основе предположения, что реша- ющую роль во внешнем массообмене играет раз- рушение пограничного слоя мелкомасштабными турбулентными пульсациями: 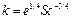 , где e –удельная диссипация механической энергии; Sc – критерий Шмидта.
, где e –удельная диссипация механической энергии; Sc – критерий Шмидта.



