Одной из актуальных задач мониторинга частотного ресурса, связанных с эффективным использованием спутников-ретрансляторов, расположенных на геостационарных орбитах (ГСО), яв- ляется противодействие несанкционированному использованию, как правило, с хакерским взломом защиты. И тогда встает вопрос об идентификации передатчика. При этом расположенные на Земле источники помех используют спутниковый канал по линии вверх, а сигнал по линии вниз будет восприниматься как помеха.
Методы определения местоположения передатчиков на поверхности Земли для спутников на ГСО
Определение местоположения несанкционированных наземных радиопередатчиков, затрагивающих спутники связи на ГСО, является сложной задачей, которая обычно выполняется путем анализа временной задержки сигнала (ВЗС) и доплеров-ского смещения частоты (ДСЧ) сигнала. Общее описание этих подходов приведено в [1].
При проведении измерений для повышения точности определения координат источника помех может использоваться сигнал от второго спутника ГСО, если он попадает в луч передатчика станции помехи. Земных станций приема сигналов от спутников также может быть две и более, при этом земные станции должны быть синхронизированы.
 Рассмотрим предельные показатели эффективности определения местоположения передатчиков на поверхности Земли с помощью одного спутника на ГСО и обратного доплеровского сдвига [1–6] (рис. 1).
Рассмотрим предельные показатели эффективности определения местоположения передатчиков на поверхности Земли с помощью одного спутника на ГСО и обратного доплеровского сдвига [1–6] (рис. 1).
Местоположение передатчика (или источника помех) на поверхности Земли можно определить при конкретных условиях, используя сигналы передатчика, ретранслируемые через одиночный спутник связи на ГСО. Небольшой доплеровский сдвиг несущей частоты сигнала, вызванный небольшим перемещением данного спутника на орбите относительно поверхности Земли, можно использовать для расчета местоположения передатчика вплоть до указания определенной точки (в пределах десятков километров), где можно развернуть подвижные средства для точного установления местоположения передатчика или источника помех. В этой методике используются измерения несущей частоты нерегулярных кратковременных передач, разнесенных по времени на несколько часов. Для оценки с необходимой степенью точности малого доплеровского сдвига в передаваемых сигналах используются методы со сверхвысокой разрешающей способностью и высоким качеством обработки сигнала. Прогнозы позиций и скорости спутника могут уточняться при использовании эталонного передатчика [3].
Эксцентриситет и ненулевой наклон плоскости ГСО приводят к некоторому перемещению спутника относительно поверхности Земли. При таком перемещении создается небольшой доплеровский сдвиг, который можно использовать для расчета местоположения передатчика. В целях обеспечения необходимой точности определения координат источника помех могут использоваться наблюдения за излучениями передатчиков, разнесенными по времени на несколько часов. Чтобы можно было использовать этот метод, несущие частоты требуется измерять с очень высокой точностью.
В [1] приведено выражение для прогнозирования несущей частоты сигнала, который ретранслируется через спутник на ГСО:
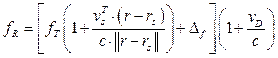 , (1)
, (1)
где fR – несущая частота принимаемого сигнала; fT – несущая частота передаваемого сигнала; vs – вектор скорости спутника в период наблюдения; rs – вектор позиции спутника в период наблюдения; r – вектор позиции передатчика; Df – транспониро-вание частоты в ретрансляторе спутника; vD – ска-лярная скорость изменения дальности между спут-ником и приемником; c – скорость распростране-ния сигнала.
Векторы rs и r определены в пространственной геоцентрической декартовой системе координат.
Для определения местоположения передатчика на поверхности Земли в алгоритме [3] используется доплеровский сдвиг частоты, который возникает на линии вверх (от источника помех на спутник) и на линии вниз (от спутника на земную станцию).
Измерения частоты на приемнике земной станции осуществляются достаточно продолжительное время. Определение местоположения источника помех на поверхности Земли выполняется на основе получаемых оценок доплеровского смещения частоты, для чего следует использовать алгоритмы марковской теории оптимальной нелинейной фильтрации в дискретном времени [7]. Эти алгоритмы основаны на накоплении полезной информации о параметрах сигнала, которые содержатся в апостериорной плотности вероятности.
В настоящей работе основное внимание сосредоточено на потенциальной точности оценок и на выборе эффективного в смысле минимума энтропии покрытия [8] подхода.
В алгоритме для определения местоположения на поверхности Земли на основе выражения (1) применим линеаризованный вариант выражения принимаемой частоты, для чего используем разложение правой части выражения (1) в ряд Тейлора и ограничимся членами первого порядка малости. В результате придем к системе линейных уравнений с представлением в виде матричного урав- нения [1, 3–5]:
F=DA, (2)
где F – вектор совокупности k измерений несущей частоты принятого сигнала: Ft = (f1, f2, …, fk); t – знак транспонирования; At= [Af Ax Ay AZ]t, каждый вектор-столбец A является производной правой части выражения (1) по каждому параметру:
 ,
,
 ,
,
 ,
,

где D – матрица размером k´4 погрешностей между истинными и оценочными значениями параметров f, x, y, z на каждом из k моментов времени.
Данное матричное уравнение используется в качестве детерминированной составляющей в уравнении наблюдения для алгоритмов квазиоптимальной нелинейной фильтрации, использующих расширенный дискретный фильтр Калмана [8].
Точность результатов определения местоположения на поверхности Земли зависит от погрешности определения векторов позиции и скорости спутника во время каждого сеанса наблюдения. Векторы обычно вычисляются на основе модели движения по орбите и совокупности из шести орбитальных элементов, которые характеризуют орбиту спутника. Элементы периодически уточняются на основе наблюдений спутника и полученных совокупностей элементов орбиты. Алгоритмами движения по орбите моделируется влияние гравитационных полей Земли, Солнца и Луны для прогнозирования позиции и скорости спутника на более длительные периоды времени, чем то время, на которое эти элементы были вычислены [6].
Информационная оценка эффективности измерений с использованием энтропии покрытия
Выражение (1) в правой части содержит в качестве неизвестных параметров как вектор координат r, так и частоту передатчика fT. Для оценки потенциальной точности целесообразно разнести эти параметры в разные части равенства:
 . (3)
. (3)
В выражении (3) значение c/fT представим длиной радиоволны передатчика λT:
 . (4)
. (4)
В левой части выражения (4) случайной величиной является параметр λT, а в правой части – вектор координат передатчика r. В алгоритме определения координат [3] применена линеаризация выражения (1) путем разложения его правой части в ряд Тейлора с оставлением членов первого порядка малости. Для правой части выражения (4) также следует применить разложение в ряд Тейлора по вектору r с оставлением членов первого порядка малости. Тогда будет справедливо допущение о подобности законов распределения для λT и r, поскольку λT будет линейной комбинацией от компонентов вектора r.
В качестве параметрического шума для частоты сигнала будем использовать аддитивный белый гауссовский шум. Тогда плотность распределения примет вид:
 , (5)
, (5)
где sf – среднеквадратическое отклонение (СКО) значений частоты; mf – математическое ожидание значения частоты с учетом доплеровского сдвига.
Поскольку параметр λT функционально связан с fT, его плотность распределения как плотность распределения функции случайной величины может быть определена следующим образом:
 . (6)
. (6)
С использованием неравенства Крамера–Рао может быть получено значение СКО для потенциальных оценок измерения доплеровского смещения частоты:
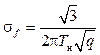 , (7)
, (7)
где q=2E/N0 – отношение сигнал/шум по энергии сигнала; Tн – интервал времени наблюдения сигнала.
Для уточненных элементов орбиты геостационарного спутника в примере, приведенном в [1], использованы значения частот от 248,934968 МГц до 248,934974 МГц. Доплеровское смещение частоты составляет примерно 6 Гц, sf ≈ 8,71728E-05 Гц, sλ ≈ 1,83E+10 м.
 Будем использовать эти данные для проведения оценки эффективности измерений. В этом случае с учетом того, что погрешности определения дальности и измерения частоты пропорциональны, получаем, что при отношении сигнал/шум 10 дБ значение СКО по дальности составит sD ≈ 523,04 м. График плотности распределения вероятностей для измерений длины волны передатчика представлен на рисунке 2.
Будем использовать эти данные для проведения оценки эффективности измерений. В этом случае с учетом того, что погрешности определения дальности и измерения частоты пропорциональны, получаем, что при отношении сигнал/шум 10 дБ значение СКО по дальности составит sD ≈ 523,04 м. График плотности распределения вероятностей для измерений длины волны передатчика представлен на рисунке 2.
Из приведенного материала видно, что время сеанса проведения измерений, отношение сигнал/шум и параметры проведения измерений взаимосвязаны между собой. Возникает вопрос об оптимизации измерений. Ясно, что, чем дольше проводить измерения, тем меньше их погрешности. Но несанкционированные передачи могут быть как кратковременными (до нескольких секунд), так и достаточно продолжительными (до нескольких часов). Для информационной оценки эффективности необходимо задать тактико-технические требования по нормативной длительности наблюдения и нормативному СКО оценки дальности. Тогда можно использовать информационную меру – энтропию покрытия [7–9]: Hп (Dр) = klog {||CDрDтÈ ÈDт||2 / ||Dт||2}, где CDр – операция дополнения к множеству реальных технических показателей Dр; Dт – множество требуемых технических показателей; ||×||2 – вторая норма. Коэффициент k определяет единицы измерения энтропии покрытия. Для двоичного логарифма энтропия покрытия измеряется в битах.
Энтропию покрытия в рассматриваемом случае доопределим следующим образом:
 , (8)
, (8)
где Tнорм и sDнорм – нормативные значения времени наблюдения и СКО дальности соответственно.
Энтропия покрытия характеризует эффективность систем, которые могут быть представлены вектором показателей эффективности, в соответствии с их целевым применением. Минимальное значение, равное нулю, означает, что нормативные требования выполнены полностью, а положительные значения характеризуют уровень обобщенного несоответствия нормативным требованиям.
С использованием энтропии покрытия была проведена оценка информационной потенциальной эффективности при обнаружении координат источника помех с использованием эффекта доплеровского сдвига частоты. В качестве нормативного значения времени наблюдения использовано значение 10 сек., а в качестве нормативно допустимой погрешности измерения дальности использованы значения 100 и 1 000 метров. Результаты компьютерного моделирования при различных значениях сигнал/шум представлены на рисунках 3 и 4.


По результатам компьютерного моделирования можно сделать вывод, что оптимальный минимум энтропии покрытия связан со значением сигнал/шум в канале приема. При этом для нормативного СКО определения дальности 100 метров оптимальное время наблюдения должно составлять от 100 до 400 секунд, а для СКО определения дальности 1 000 метров – от 55 до 100 секунд.
Энтропия покрытия позволяет не допускать лишних затрат на поиски источника помех, когда заданы требуемые точностные характеристики.
Работа выполнена при поддержке РФФИ, грант № 16-07-00511.
Литература
1. Handbook on Spectrum Monitoring. ITU, Switzerland, Geneva, 2011, pp. 374–387.
2. Черняк В.С. Многопозиционная радиолокация. М.: Радио и связь, 1993. 416 с.
3. Koets M.A., Bentley R.T. Satellite based geolocation using a single geosynchronous satellite and an inverse doppler technique. SRI Publ., USA, S.A., 1999.
4. Ковалев А.Н., Ковалев Ф.Н. Потенциальная точность определения параметров траектории цели в просветном бистатическом радиолокаторе // Тр. НГТУ им. Р.Е. Алексеева. 2014. Т. 104. № 2. С. 17–22.
5. Рындык А.Г., Сидоров С.Б., Бляхман А.Б., Ковалев Ф.Н. Точность определения координат методом максимального правдоподобия при локации «на просвет» // Радиотехника и электроника. 1999. Т. 44. № 12. С. 1436–1440.
6. Алипбаев К.А. Моделирование движения геостационарного спутника // Вестн. КазНТУ. 2011. № 6. C. 120–122.
7. Ломакин М.И., Коровайцев А.А., Сухов А.В. Информационно-энтропийный подход к оценке метрологического ресурса средств измерений // Измерительная техника. 2014. № 6. С. 14–17.
8. Сухов А.В. Динамика информационных потоков в системе управления сложным техническим комплексом // Теория и системы управления. 2000. № 4. С. 111–120.

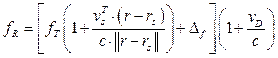 , (1)
, (1) ,
, ,
, ,
,
 . (3)
. (3) . (4)
. (4) , (5)
, (5) . (6)
. (6)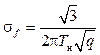 , (7)
, (7)
 , (8)
, (8)

