Во время движения летательный аппарат (ЛА) создает вихревые возмущения, которые остаются вдоль траектории его полета. Совокупность этих возмущений формирует турбулентный (вихревой) след ЛА [1], который со временем эволюционирует и в конечном итоге разрушается [2]. Пока вихревой след существует, он может представлять опасность для других участников воздушного движения при попадании их в данный след [3]. Особенно это критично в местах скопления ЛА, где на небольшом участке пространства может находиться сразу большое количество вихревых следов (аэродромы) [4]. Поэтому необходимо осуществлять постоянный мониторинг вихревых следов вплоть до их разрушения и оценивать опасность их влияния на собственный ЛА [5]. В данной статье рассматривается задача определения потенциальных конфликтов с множеством вихревых следов ЛА. Приводится алгоритм решения данной задачи, а также рассматривается его реализация на вычислителе Intel Xeon Phi.
Постановка задачи
Траекторию движения ЛА зададим набором точек в пространстве, последовательно соединенных отрезками. Будем считать, что в данных точках известны характеристики ЛА, в том числе и интенсивность создаваемых им вихревых возмущений, а также то, что опасная зона одной конкретной точки представляет собой шар с центром в этой точке. Точку в трехмерном пространстве зададим радиус-вектором, направленным из начала координат в эту точку, а сферу – ее центром и радиусом следующим образом: 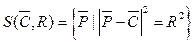 .
.
Примем, что опасная зона отрезка является объединением опасных зон всех его точек, где радиус опасной зоны точки отрезка меняется линейно от одного его конца до другого. Для задания опасной зоны отрезка введем понятие пучка сфер, опирающегося на две различные сферы. Пусть заданы две сферы:  .
.
Тогда пучком сфер, опирающимся на них, назовем такое множество сфер, центры и радиусы которых определяются следующим образом:

где параметр α изменяется от 0 до 1. Нетрудно заметить, что опасная зона отрезка представляет собой область, ограниченную опасными зонами его концов, являющимися шарами, и множеством общих внешних касательных данных шаров. Кроме того, отметим, что опасная зона отрезка является выпуклым телом. Опасную зону всей траектории движения ЛА будем определять как объединение опасных зон всех отрезков его движения
 На рисунке 1 показан пример траектории движения ЛА, закрашенными кругами обозначены опасные зоны точек, в которых известны характеристики ЛА, также очерчена опасная зона всей траектории движения.
На рисунке 1 показан пример траектории движения ЛА, закрашенными кругами обозначены опасные зоны точек, в которых известны характеристики ЛА, также очерчена опасная зона всей траектории движения.
Итак, в задаче обнаружения возможных кон- фликтов с опасными зонами траекторий движения в местах скопления ЛА задаются множество траекторий движения различных ЛА, а также положение и вектор мгновенной скорости собственного ЛА, для которого нужно определить конфликт. Положение и вектор скорости собственного ЛА определяют луч, состоящий из множества точек  при t ³ 0, для которого нужно определить, пересекает ли он опасную зону траектории движения хотя бы одного ЛА. В случае конфликта требуется найти точку первого пересечения для определения уровня угрозы, то есть времени, оставшегося до пересечения опасной зоны.
при t ³ 0, для которого нужно определить, пересекает ли он опасную зону траектории движения хотя бы одного ЛА. В случае конфликта требуется найти точку первого пересечения для определения уровня угрозы, то есть времени, оставшегося до пересечения опасной зоны.
Решение
Для решения поставленной задачи необходимо решить задачу пересечения прямой с пучком сфер. Сначала рассмотрим пересечение прямой и отдельной сферы. Без ограничения общности будем считать, что собственный ЛА находится в начале координат (этого всегда можно добиться с помощью параллельного переноса). Пересечение прямой со сферой находится из следующей системы уравнений:

Данная система уравнений преобразуется в квадратное уравнение относительно t, дискриминант которого равен  .
.
Так как значение дискриминанта может быть вычислено непосредственно, дальнейшее нахождение точек пересечения не представляет труда (если он неотрицательный).
Перейдем к поиску точек пересечения прямой и пучка сфер. Для каждой конкретной сферы из пучка можно выписать условие наличия точек пересечения:
 .
.
Подставив конкретные выражения для центра и радиуса сферы и выполнив необходимые преобразования, получим квадратное неравенство относительно параметра α:  , где
, где 
Полученное неравенство можно решить относительно α, так как все коэффициенты вычисляются непосредственно. Нас интересует решение данного неравенства только на отрезке [0, 1], оно представляет собой либо пустое множество, либо отрезок.
Если на отрезке [0, 1] приведенное неравенство не имеет решения, прямая не пересекает пучок сфер. Допустим, на отрезке [0, 1] данное неравенство имеет решение [a0, a1] Í [0, 1].
Для произвольного значения α из данного отрезка корни уравнения

существуют и выражаются следующим образом:
 .
.
Искомые точки пересечения прямой с пучком сфер соответствуют минимальному и максимальному значениям параметра t(a), достигаемым на отрезке [a0, a1]. Максимальное и минимальное значения t(a) могут достигаться либо на концах отрезка, либо в точках локального экстремума. Для точки локального экстремума должно быть выполнено соотношение t’1,2(a) = 0 или в явном виде

После преобразования получим следующее квадратное уравнение относительно α:
 ,
,
решая которое, найдем потенциальные точки локальных экстремумов  .
.
Данные точки нужно учитывать только в случае их попадания в отрезок [a0, a1]. В общем случае значения находятся по четырем значениям α:
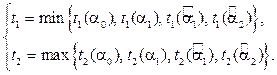
По найденным значениям непосредственно находятся точки пересечения прямой с пучком сфер. Для задачи, рассматриваемой в статье, необходимо получить ответ о пересечении с пучком сфер не на всей прямой, а на луче, соответствующем неотрицательным t. Конечно, возможен случай, когда собственный ЛА уже находится в опасной зоне и пересечение с данной опасной зоной произошло при t < 0, но данный случай легко сво- дится к общему.
Особенности решения
Рассмотрим подробнее решение представленного ранее квадратного неравенства A2a2+2A1a + + A0 ³ 0.
Утверждалось, что решением данного неравенства на отрезке [0, 1] является либо пустое множество, либо отрезок. Единственным потенциально возможным вариантом, когда это не так, является вариант, при котором A2 > 0 и оба значения α, при которых неравенство обращается в равенство, находятся внутри отрезка [0, 1]. Это означает, что прямая пересекает сферы S0 и S1, однако не пересекает хотя бы одну другую сферу из пучка. Но это невозможно в силу выпуклости пучка сфер, а значит, этот случай исключен.
Теперь рассмотрим подробнее случай A2 < 0:
 .
.
Раскрыв скалярное произведение векторов и выполнив необходимые преобразования, получим следующее условие на угол между скоростью собственного ЛА и отрезком, содержащим центры сфер пучка:  , где
, где  представляет собой синус угла раствора пучка сфер. Заметим, что данный угол раствора всегда очень мал, так как характеристики ЛА меняются медленно во время движения и ½DR½ близко к нулю. Таким образом, случай A2 < 0 является наиболее частым и данное условие выполняется в подавляющем большинстве случаев (рис. 2).
представляет собой синус угла раствора пучка сфер. Заметим, что данный угол раствора всегда очень мал, так как характеристики ЛА меняются медленно во время движения и ½DR½ близко к нулю. Таким образом, случай A2 < 0 является наиболее частым и данное условие выполняется в подавляющем большинстве случаев (рис. 2).

Программная реализация и оптимизация
Опишем программную реализацию функции, которая по набору пучков сфер выдает координаты точек пересечения с ними. Для простоты будем считать, что задана только одна траектория движе- ния ЛА. Входными данными функции являются четыре массива: три массива с координатами точек, последовательно соединенных отрезками (x, y, z), и один массив с радиусами опасных зон этих то- чек (r). Также на вход подается вектор скорости собственного ЛА. Тогда алгоритм поиска точек пересечения с одним пучком сфер можно записать в виде следующей последовательности шагов.
1. Вычислить коэффициенты A2, A1, A0, фигурирующие в квадратном неравенстве.
2. Если A2 > 0, решить квадратное неравенство на отрезке [0,1] и перейти к п. 5, иначе перейти к п. 3.
3. Если A2 < 0, решить квадратное неравенство на отрезке [0, 1] и перейти к п. 5, иначе перейти к п. 4.
4. Так как A2 = 0, решить линейное неравенство на отрезке [0, 1] и перейти к п. 5.
5. Если решение неравенства из пп. 2–4 на отрезке [0, 1] пусто, перейти к следующему пучку сфер, иначе перейти к п. 6.
6. На отрезке [a0, a1], найденном в пп. 2–4, найти точки, в которых значения t1,2 достигают своих экстремумов.
7. По значениям  в общем случае найти моменты времени пересечения прямой с пучком сфер.
в общем случае найти моменты времени пересечения прямой с пучком сфер.
Данный алгоритм был реализован на языке C, а исполняемые коды опробованы на ускорителях Intel Xeon Phi 7110X [6], которые входят в состав находящегося в МСЦ РАН вычислительного комплекса МВС-10П [7]. Однако полученные результаты выявили неэффективное использование возможностей ускорителя. Основной проблемой стало наличие в алгоритме довольно сложного управления. В частности, разбор различных случаев при решении квадратного неравенства и при нахождении точек экстремумов  . Такое сложное управление привело к невозможности эффективного применения векторизации в цикле обработки пучков сфер [8].
. Такое сложное управление привело к невозможности эффективного применения векторизации в цикле обработки пучков сфер [8].
Так как оптимизирующий компилятор [9] из состава Intel Parallel Studio, который использовался для компиляции кода, не смог подготовить эффективный исполняемый код, для устранения недостатков в эффективности было принято решение модифицировать код таким образом, чтобы удалить из цикла маловероятные ветви исполне- ния [10]. Как было показано выше, в подавляющем большинстве случаев при решении квадратного неравенства выполняется условие A2 < 0. Однако даже в этом случае решение квадратного неравенства на отрезке [0, 1] почти всегда представляет собой пустое множество. Переписав условие отсутствия пересечений с пучком сфер, в данном случае получим выражение, которое истинно с вероятно- стью, близкой к единице:
 ,
,
где m = max(A1 + A2, –A1). Если обозначить это вероятное условие через cond, можно переписать основной цикл обработки пучков сфер в следующем виде:
for (<цикл по всем пучкам сфер>)
{
<вычисления>
if (cond)
{
continue; // prob. ~100%
}
else
{
<маловероятные вычисления>
}
}
Данный цикл можно расщепить на два цикла, используя дополнительный массив, содержащий значения условий cond. При этом получим следующий результат:
for (<цикл по всем пучкам сфер>)
{
<вычисления>
tmp[i] = cond;
}
for (<цикл по всем пучкам сфер>)
{
if (!tmp[i])
{
<маловероятные вычисления>
}
}
В оптимизированном варианте основная часть вычислений приходится на первый цикл, при этом он не содержит сложного управления, а значит, подходит для векторизации. Второй цикл, конечно, неэффективно исполняется на ускорителе, но его время исполнения настолько мало, что им можно пренебречь.
Были проведены сравнительные запуски с моделированием случайных траекторий движения ЛА для неоптимизированного и оптимизированного вариантов и получены стабильные результаты, которые демонстрируют ускорение вычислений за счет векторизации более чем в 5 раз по сравнению с неоптимизированным вариантом.
 На рисунке 3 представлены результаты запусков. По горизонтальной оси отмечены 10 запусков, каждый из которых состоял из обработки 107 пучков сфер. По вертикали указано ускорение, полученное при использовании векторизованного варианта по сравнению с исходным.
На рисунке 3 представлены результаты запусков. По горизонтальной оси отмечены 10 запусков, каждый из которых состоял из обработки 107 пучков сфер. По вертикали указано ускорение, полученное при использовании векторизованного варианта по сравнению с исходным.
Заключение
При решении реальных практических задач с применением современных аппаратных вычислительных ресурсов сложно ожидать эффективного исполнения программы даже при использовании высококачественного компилятора, способного проводить оптимизацию кода. Зачастую задача требует вмешательства исследователя, способного определить особенности алгоритма и должным образом использовать их. Часто небольшие из- менения логики вычислений, не влияющие на результат, но использующие особенности алгоритма, способны привести к кратному повышению производительности.
Литература
1. Аубакиров Т.О., Желанников А.И., Иванов П.Е., Ништ М.И. Спутные следы и их воздействие на летательные аппараты. Моделирование на ЭВМ. Алматы: Гылым, 1999. 280 с.
2. Вышинский В.В., Судаков Г.Г. Вихревой след самолета в турбулентной атмосфере // Тр. ЦАГИ. 2006. Вып. 2667. 155 с.
3. Бабкин В.И., Белоцерковский А.С., Турчак Л.И., Баранов Н.А., Замятин А.И., Каневский М.И., Морозов В.В., Пасекунов И.В., Чижов Н.Ю. Системы обеспечения вихревой безопасности полетов летательных аппаратов. М.: Наука, 2008. 373 с.
4. Бурлуцкий С.Г. Вопросы обеспечения вихревой безопасности аэропортов // Системный анализ и логистика. 2014. № 11. С. 37–40.
5. Кудрявцев Н.С. Оценка эффективности систем обеспечения вихревой безопасности полетов // Естественные и математические науки в современном мире. 2016. № 11. С. 31–37.
6. Jeffers J., Reinders J. Intel Xeon Phi coprocessor high performance programming. Morgan Kaufmann Publ., 2013, 432 p.
7. Описание интерфейса пользователя, предназначенного для работы с интеловской гибридной архитектурой суперЭВМ... URL: http://www.jscc.ru/informat/MVS-10PInter.pdf (дата обращения: 15.05.2017).
8. Шабанов Б.М., Телегин П.Н., Аладышев О.С. Особенности использования многоядерных процессоров // Програм- мные продукты и системы. 2008. № 2. С. 7–9.
9. Aho A.V., Lam M.S., Sethi R., Ullman J.D. Compilers: principles, techniques, and tools (2nd Ed.). Pearson Education Inc. Publ., 2006, 1038 p. 10. Allen R., Kennedy K. Optimizing compilers for modern architectures. Morgan Kaufmann Publ., 2001, 790 p.
10. Allen R., Kennedy K. Optimizing compilers for modern architectures. Morgan Kaufmann Publ., 2001, 790 p.
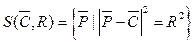 .
. .
.

 при t ³ 0, для которого нужно определить, пересекает ли он опасную зону траектории движения хотя бы одного ЛА. В случае конфликта требуется найти точку первого пересечения для определения уровня угрозы, то есть времени, оставшегося до пересечения опасной зоны.
при t ³ 0, для которого нужно определить, пересекает ли он опасную зону траектории движения хотя бы одного ЛА. В случае конфликта требуется найти точку первого пересечения для определения уровня угрозы, то есть времени, оставшегося до пересечения опасной зоны.
 .
. .
. , где
, где 

 .
.
 ,
, .
.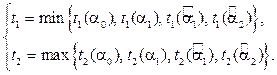
 .
. , где
, где  представляет собой синус угла раствора пучка сфер. Заметим, что данный угол раствора всегда очень мал, так как характеристики ЛА меняются медленно во время движения и ½DR½ близко к нулю. Таким образом, случай A2 < 0 является наиболее частым и данное условие выполняется в подавляющем большинстве случаев (рис. 2).
представляет собой синус угла раствора пучка сфер. Заметим, что данный угол раствора всегда очень мал, так как характеристики ЛА меняются медленно во время движения и ½DR½ близко к нулю. Таким образом, случай A2 < 0 является наиболее частым и данное условие выполняется в подавляющем большинстве случаев (рис. 2).
 в общем случае найти моменты времени пересечения прямой с пучком сфер.
в общем случае найти моменты времени пересечения прямой с пучком сфер. . Такое сложное управление привело к невозможности эффективного применения векторизации в цикле обработки пучков сфер [8].
. Такое сложное управление привело к невозможности эффективного применения векторизации в цикле обработки пучков сфер [8]. ,
,
