Поводом для данного исследования послужило привлекшее внимание сообщение в Интернете. Прочтите его не по буквам и не по слогам, а как обычно читаете тексты.
По рзелульаттам илссеовадний одонго анлигйсокго унвиертисета, не иеемт занчнеия, в кокам пряоддке рсапожплены бкувы в солве. Осатьлыне бкувы мгоут селдовтаь в плоонм бсепордяке, все рвано ткест чтаитсея без побрелм. Пичрионй эгото ялвятеся то, что мы не чиатем кдаужю бкуву по отдльенотси, а все солво цликеом.
Составив на английском, литовском, русском, таджикском языках и на языке эсперанто разнообразные тексты, делая во всех словах случайные перестановки букв и выставив такое творчество на обозрение, можно убедиться в том, что респонденты без затруднений понимают содержание полученного «произведения».
Постановка задачи
Примем, что текст какого-либо естественного языка является анаграммно искаженным, если каждому его слову сопоставлен набор из тех же самых букв, но расставленных в произвольном порядке. Фрагмент из Интернета как раз является примером такого текста. Каким же образом человеческий мозг легко справляется с его прочтением, восприятием и пониманием?
Предлагаемая далее математическая модель распознавания мозгом содержания искаженного текста основывается на гипотезе (упрощенной), состоящей из трех пунктов:
- мозг воспринимает текст пословно;
- мозг распознает слово правильно, если из заданного набора букв может быть составлено одно и только одно слово;
- мозг допускает ошибку, если из заданного набора букв может быть составлено несколько слов.
В двух последних пунктах в неявном виде просматривается понятие анаграммы. Поскольку в настоящей статье оно будет использоваться в несколько нетрадиционном смысле, приведем вначале два общеизвестных определения.
В энциклопедии анаграмма означает слово или словосочетание, образованное перестановкой букв другого слова или словосочетания.
В толковом словаре русского языка анаграм- ма – это перестановка букв, посредством которой из одного слова составляется другое.
Из первого определения следует, что анаграм- ма – слово, а из второго – процедура (перестановка букв). В дальнейшем будем пользоваться обоими определениями, а также и следующим: анаграм- ма – это конечное множество (по крайней мере, пара) слов естественного языка, составленных из одного и того же набора букв.
Анаграмму естественно называть тривиальной, если она состоит из одного элемента-слова. Рассмотрим, как обстоит дело с нетривиальными анаграммами в некоторых языках.
Инструмент для формирования подмножеств словоформных анаграмм
Пусть L – естественный язык с алфавитом A и W = ²a1a2 … an² – некоторое слово длины n, состоящее из букв ak Î A. Рассмотрим цепочку CW = = ²as1as2 … asn², составленную из тех же самых букв, что и слово W, но упорядоченных по алфавиту.
Определение 1. Отображение F: W ® CW назовем упорядоченным алфавитным кодированием (ab-кодированием) слова W, а цепочку букв CW – его ab-кодом [1].
Для пояснения определения укажем, что ab-кодирование, например, слова W = “реферат” приводит к цепочке  = “аеерртф”, а слова W = = “агент” − к той же самой цепочке CW = “агент”, поскольку в этом слове буквы уже расположены в алфавитном порядке.
= “аеерртф”, а слова W = = “агент” − к той же самой цепочке CW = “агент”, поскольку в этом слове буквы уже расположены в алфавитном порядке.
Кодирующее отображение F: W ® CW является однозначным, декодирующее F–1: CW ® W, вообще говоря, является многозначным, поскольку коду могут соответствовать несколько словоформ. Нарушение однозначности происходит на образах анаграмм. Например, цепочке букв CW = = “иикопрт” соответствует анаграмма из двух прообразов (тропики − киприот).
Всякой анаграмме соответствует единственный образ, соответствующий ab-код. Этот факт подсказывает простой способ извлечения множества словоформных анаграмм из какого-либо текста. Вначале следует построить частотный словарь словоформ, затем каждой словоформе сопоставить ее ab-код и, наконец, скомпоновать в подмножества словоформы с одинаковыми ab-кодами.
Исследование декодирующего отображения F–1
Обратимся к таблице 1. В ней в 1-м столбце представлен список языков, во 2-м – размеры (в словах) коллекций текстов. Результаты обработки исходных данных приведены в последующих столбцах: в 3-м указывается число различных словоформ, обнаруженных в коллекциях; в 4-м – число различных ab-кодов словоформ; в 5-м и 6-м из общего числа кодов выделяются однозначные и многозначные, а в 7-м и 8-м столбцах данные 5-го и 6-го столбцов показаны в процентах.
Из столбцов 5–6 и 7–8 таблицы 1 видно, что для рассматриваемых языков количество однозначно декодируемых кодов на порядок больше суммарного количества кодов анаграмм. Полученный результат, отдавая приоритет однозначно декодируемым кодам, создает искаженную картину об обратном отображении F–1, ибо не принимает в расчет частотности кодов и тех, и других.
Уточненные свойства F–1 выявляются в столб- цах 4 и 6 таблицы 2. Действительно, в этих столб- цах приводятся данные о суммарных частотах встречаемости однозначно декодируемых и двусмысленных (многозначных) кодов для соответствующих коллекций. Эти данные, пересчитанные в столбцах 4 и 6 в процентах, показывают недостаточно приемлемый для практических целей уровень декодирования слов, реализуемый отображением F–1: относительные частоты встречаемости элементов анаграмм для отмеченных языков группируются вокруг значения 0,5. Иначе говоря, почти каждое второе слово из корпуса текстов принадлежит множеству анаграмм.

Определение модифицированного отображения F(*)
Итак, ab-кодирование, будучи удобным средством для выявления всевозможных элементов анаграмм, оказывается неэффективным для декодирования. В связи с этим обратимся к отображению F(*), которое наделим следующими свойствами [1]:
- как и F, оно определено на множестве {W} слов естественного языка L;
- как и F, оно ставит в соответствие слову W его ab-код, то есть F(*): W ® CW;
- обратное отображение  на множестве однозначно декодируемых кодов совпадает с F–1, а на множестве многозначных кодов (образов анаграмм) каждому образу CW ставит в соответствие единственное слово W*, которое имеет максимальную частоту встречаемости в текстах в сравнении с другими словами из набора слов рассматриваемой анаграммы.
на множестве однозначно декодируемых кодов совпадает с F–1, а на множестве многозначных кодов (образов анаграмм) каждому образу CW ставит в соответствие единственное слово W*, которое имеет максимальную частоту встречаемости в текстах в сравнении с другими словами из набора слов рассматриваемой анаграммы.
Последнее свойство назовем F(*)-схемой декодирования. Очевидно, что принятие решений по этой схеме имеет вероятностный характер и предполагает возможность допущения ошибки в случаях, когда при правильном декодировании на выходе должно появиться слово не с максимальной частотой.
Практическое использование отображения F(*) предполагает наличие развитой БД {W Û CW}, реализующей взаимно однозначное соответствие между элементами множеств {W} и {CW}. Поскольку установление такого соответствия основывается на отмеченных свойствах функции F(*), ее априорную эффективность естественно определять суммарной частотой слов, ab-коды которых декодируются по F(*)-схеме. Соответствующие данные, приведенные в столбцах 7 и 8 таблицы 2, указывают на высокий уровень такого декодирования (не менее 94 % для эсперанто и 97 % для других языков).
Итак, F(*)-отображение можно трактовать как математическую модель работы распознающего мозга. Действительно, всякий раз, когда приходится иметь дело с очередным «сумбурным» сло- вом, мозг интуитивно сопоставляет ему то един- ственное слово (с той же самой совокупностью букв), которое встречалось в его практике чаще других слов из их общей анаграммы. Именно такое свойство мозга заключено в F(*)-схеме.
Обратим внимание еще на одну важную сторону F(*)-отображения. Оно указывает, что исследование (а фактически заключение) «…одного английского университета», представленное во введении настоящей статьи, является неточным: для понимания анаграммно испорченного текста нет никакой необходимости фиксировать неподвижными первую и последнюю буквы слова (остальные перемешивать произвольно).
Далее рассмотрим другие модели понимания текста, которые в сравнении с F(*)-моделью подчиняются дополнительным ограничениям. Априори очевидно, что такие модели будут иметь более высокий процент безошибочного восприятия текстов, однако, как будет показано далее, повышение точности не будет столь принципиальным.
F(*)-модель распознавания текста (фиксируются неизменными первые буквы слов).
Функция F(f) задается на множестве {W} слов естественного языка L.
Определение 2. Отображение F(f) слову W ставит в соответствие цепочку a1C(W/a1), в которой a1 – первая буква в слове W и C(W/a1) − ab-код цепочки W/a1, то есть слова W без первой буквы.
В отличие от F это отображение оставляет в слове W неизменной первую букву, то есть a1, и упорядочивает по алфавиту прочие буквы. Из общих соображений ясно, что декодирование a1C(W/a1) ® W в определенном смысле обладает лучшими свойствами, чем CW ® W.
Пример. Обратимся к анаграмме {W: W = автор, втора, отвар, рвота, тавро, товар}. Отображение F(f) первые четыре элемента кодирует следующим образом: аворт, ваорт, оаврт, равот, оставляя неизменными первые буквы элементов анаграммы (отмечены жирным шрифтом) и располагая в алфавитном порядке прочие буквы. Этим кодам однозначно соответствуют первые четыре элемента анаграммы. Пятый и шестой элементы анаграммы кодируются одинаково – тавро.
F(f,l)-модель распознавания текста (не измене- ны первые и последние буквы слов).
Как и F(f), функция F(f,l) задается на множестве {W} слов естественного языка L.
Определение 3. F(f,l) : W ® a1C(W/{a1, an})an.
В нем a1 – первая и an – последняя буквы слова W остаются неподвижными, а цепочка букв между ними, то есть W/{a1, an}, подвергается ab-кодированию.
Теперь рассмотрим применение отображения F(f,l) к той же анаграмме, что и в примере для F(f). В этом случае первая и последняя буквы (далее показаны жирным шрифтом) элементов анаграмм должны оставаться неизменными, а все другие буквы упорядочиваются по алфавиту. Результаты кодирования записываются в виде: авотр, ворта, оавтр, рвота, тавро, тавор, то есть все шесть слов рассматриваемой анаграммы получили собственные коды. Декодирование с помощью обратной функции также однозначно.
 Итак, в сравнении с F отображения F(f) и F(f,l) несколько сложнее, зато наверняка успешнее в вопросах декодирования (см. табл. 3). Отметим также, что F(f,l) – именно то отображение, о котором шла речь в начале статьи.
Итак, в сравнении с F отображения F(f) и F(f,l) несколько сложнее, зато наверняка успешнее в вопросах декодирования (см. табл. 3). Отметим также, что F(f,l) – именно то отображение, о котором шла речь в начале статьи.
Отметим, что для отображения F речь идет об анаграммах в смысле приведенного определения, а для отображений F(f) и F(f,l) – о соответствующим образом модернизированных анаграммах.
Замечание относительно отображений F(f) и F(f,l)
Из данных столбцов 8 и 9 видно, что для рассматриваемых языков количество различных однозначно декодируемых кодов на порядок больше суммарного количества различных кодов анаграмм. Отметим, что здесь имеется в виду список слов частотных словарей, причем без учета частот их встречаемости. Полученный результат, отмечающий высокий процент однозначно декодируемых кодов, создает, однако, искаженную картину мощности множества слов, входящих в состав анаграмм. Сделанный вывод подтверждает дальнейшее исследование, результаты которого представлены в таблице 4.

Прежде чем переходить к рассмотрению этой таблицы, объясним смысл обозначений  ,
,  и
и  . Как отмечалось ранее, отображения F, F(f) и F(f,l) каждому слову приписывают единственный код, однако обратные отображения в общем случае не обеспечивают однозначного декодирования. Использование отображений
. Как отмечалось ранее, отображения F, F(f) и F(f,l) каждому слову приписывают единственный код, однако обратные отображения в общем случае не обеспечивают однозначного декодирования. Использование отображений  ,
,  и
и  – это по существу попытка устранения неоднозначности при декодировании анаграмм и распознавании порождающих их прообразов за счет использования дополнительных атрибутов, присоединяемых к ab-кодированию.
– это по существу попытка устранения неоднозначности при декодировании анаграмм и распознавании порождающих их прообразов за счет использования дополнительных атрибутов, присоединяемых к ab-кодированию.
Определения отображений 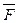 ,
,  и
и 
Определение 4. Отображения  ,
,  и
и  обладают следующими свойствами:
обладают следующими свойствами:
- задаются на множестве слов {W} языка L;
- совпадают, соответственно, с F, F(f) и F(f,l) при кодировании слов;
- их обратные отображения  ,
,  и
и  на кодах, однозначно декодируемых, совпадают, соответственно, с F–1, (F(f))–1, (F(f,l))–1, а на кодах анаграмм каждому из них ставят в соответствие единственное слово W*, которое имеет максимальную частоту встречаемости в текстах в сравнении с другими словами с одинаковым кодом.
на кодах, однозначно декодируемых, совпадают, соответственно, с F–1, (F(f))–1, (F(f,l))–1, а на кодах анаграмм каждому из них ставят в соответствие единственное слово W*, которое имеет максимальную частоту встречаемости в текстах в сравнении с другими словами с одинаковым кодом.
Пример. Положим, что в анаграмме {W: W = казан, казна, наказ} наибольшую частоту в корпусе текстов имеют слово наказ, затем казна. При отображении F (= 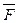 ) рассматриваемой анаграмме будет соответствовать код аазкн, которому отображение
) рассматриваемой анаграмме будет соответствовать код аазкн, которому отображение 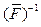 поставит в соответствие слово наказ.
поставит в соответствие слово наказ.
Если же применить отображение 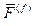 ( = F(f)), то первые два слова анаграммы получат одинаковый код каазн, а третье слово – код наазк (напомним, что при кодировании первые буквы в словах анаграмм фиксируются). Коду каазн будет сопоставляться слово казна, у которого частота больше, чем у слова казан.
( = F(f)), то первые два слова анаграммы получат одинаковый код каазн, а третье слово – код наазк (напомним, что при кодировании первые буквы в словах анаграмм фиксируются). Коду каазн будет сопоставляться слово казна, у которого частота больше, чем у слова казан.
Замечание. Предлагаемый в определении 4 метод выбора единственного прообраза того или иного кода анаграммы носит вероятностный характер. Он не исключает возможности принятия ошибочного решения в случаях, когда при правильном декодировании на выходе должно появиться слово не с максимальной частотой.
В таблице 4 приводятся результаты статистической обработки данных коллекций текстов с учетом определений трех типов кодирования словоформ.
Поясним эту таблицу. В ней первые два столб- ца – те же, что и в таблице 3. Столбец 3 отмечает три типа используемых способов кодирования слов. Столбцы 4–7 по существу продолжают таблицу 3. С учетом того, что, согласно определению 4, при кодировании слов отображения F и  F(f) и
F(f) и  F(f,l) и
F(f,l) и  совпадают, эти столбцы представляют информацию о частотах встречаемости однозначно декодируемых кодов и элементов анаграмм (многозначных кодов), причем столбцы 4 и 6 информируют об абсолютных, а 5 и 7 – об относительных значениях частот, выраженных в процентах по отношению к общему количеству слов (словоупотреблений) текстовых коллекций.
совпадают, эти столбцы представляют информацию о частотах встречаемости однозначно декодируемых кодов и элементов анаграмм (многозначных кодов), причем столбцы 4 и 6 информируют об абсолютных, а 5 и 7 – об относительных значениях частот, выраженных в процентах по отношению к общему количеству слов (словоупотреблений) текстовых коллекций.
Из данных столбцов 4–7 и пяти строк, привязанных к отображению  видно, что для всех языков, за исключением русского, слова, являющиеся элементами анаграмм, составляют более половины общего числа слов (словоупотреблений) текстовых коллекций (для русского языка – 45,69 %). По этой причине при перемешивании всех букв в слове читающий мозг будет допускать много ошибок.
видно, что для всех языков, за исключением русского, слова, являющиеся элементами анаграмм, составляют более половины общего числа слов (словоупотреблений) текстовых коллекций (для русского языка – 45,69 %). По этой причине при перемешивании всех букв в слове читающий мозг будет допускать много ошибок.
Из пяти ячеек, стоящих на пересечении столбца 7, и пяти строк, привязанных к отображению  , видно, что относительная частотность многозначных кодов располагается между значениями 17,61 % (эсперанто) и 30,52 % (литовский язык). Это и предопределяет невозможность достаточно успешного восприятия смысла слов с фиксированной первой буквой.
, видно, что относительная частотность многозначных кодов располагается между значениями 17,61 % (эсперанто) и 30,52 % (литовский язык). Это и предопределяет невозможность достаточно успешного восприятия смысла слов с фиксированной первой буквой.
Из пяти ячеек, стоящих на пересечении столбца 7, и пяти строк, привязанных к отображению  видно, что частотности многозначных кодов среди общего числа словоупотреблений равны 4,84 % и 3,75 % соответственно для эсперанто и английского языка, то есть являются относительно малыми величинами, вследствие чего читающий мозг в большинстве случаев правильно справляется с пониманием слов искаженного текста. Наряду с этим в трех других языках частотность многозначных кодов примерно на 10 % выше, поэтому ошибочность в понимании искаженных слов будет недопустимой для практического применения
видно, что частотности многозначных кодов среди общего числа словоупотреблений равны 4,84 % и 3,75 % соответственно для эсперанто и английского языка, то есть являются относительно малыми величинами, вследствие чего читающий мозг в большинстве случаев правильно справляется с пониманием слов искаженного текста. Наряду с этим в трех других языках частотность многозначных кодов примерно на 10 % выше, поэтому ошибочность в понимании искаженных слов будет недопустимой для практического применения  -модели.
-модели.
Итак, несмотря на то, что количество различных однозначно декодируемых слов (словоформ) оказалось на порядок больше количества различных слов, входящих в состав анаграмм (см. данные столбцов 8 и 9 для строк F-отображения), частоты встречаемости рассматриваемых элементов в тестовых коллекциях пяти языков оказались одного порядка.
Последние два столбца, 8-й и 9-й, таблицы 4 выдают количественные показатели эффективности декодирования в соответствии с определением 4. Для всех пяти языков ошибки принятия неверных решений заключаются в пределах 1 % при декодировании посредством  и
и  и не превосходят 3 % при декодировании с помощью
и не превосходят 3 % при декодировании с помощью  (для эсперанто – не более 6 %).
(для эсперанто – не более 6 %).
Обсуждение результатов
Итак, отображения  ,
,  и
и  можно рассматривать в качестве математических моделей функционирования мозга, распознающего смысл анаграммно искаженного текста. В согласии с этим процесс понимания мозгом произвольного набора букв происходит следующим образом:
можно рассматривать в качестве математических моделей функционирования мозга, распознающего смысл анаграммно искаженного текста. В согласии с этим процесс понимания мозгом произвольного набора букв происходит следующим образом:
- если набору букв соответствует однозначный ab-код, мозг сопоставляет ему единственную словоформу;
- если набору букв соответствует многозначный ab-код, мозг сопоставляет ему ту словоформу из анаграммы, которая имеет максимальную частоту встречаемости.
Математическая модель, описываемая отобра- жением  охватывает более общую ситуацию в сравнении с
охватывает более общую ситуацию в сравнении с  и
и 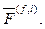 В ней нет по существу каких-либо ограничений на характер перестановок букв в слове. Вместе с тем она обеспечивает достаточно высокий уровень (не менее 97 %) распознавания смысла искаженных слов, уступая двум другим моделям в точности результата не более чем на 2 % (см. столбец 9). Если сравнивать эффективность моделей по этим двум факторам, предпочтение следовало бы отдать
В ней нет по существу каких-либо ограничений на характер перестановок букв в слове. Вместе с тем она обеспечивает достаточно высокий уровень (не менее 97 %) распознавания смысла искаженных слов, уступая двум другим моделям в точности результата не более чем на 2 % (см. столбец 9). Если сравнивать эффективность моделей по этим двум факторам, предпочтение следовало бы отдать  -отображению.
-отображению.
Гипотеза (расширенная) распознавания искаженного текста
Предложенные в настоящей статье математические модели основывались на гипотезе восприятия каждого искаженного слова в отдельности. Даже в этом случае удалось добиться почти безошибочного понимания их смысла в искаженном тексте. При необходимости достижения более точных результатов можно обратиться к цепям Маркова [2, 3], привлекая для анализа пары соседствующих слов (так называемые словоформные биграммы), которые привнесут дополнительную информацию о семантической связи слов. Последние должны быть предварительно распознаны с помощью, например,  -модели.
-модели.
Заключение
Настоящая статья по содержанию созвучна работам [4] и [5], в которых обсуждается утверждение Г. Роулинсона о том, что случайное расположение букв в середине слов либо слабо влияет, либо совсем не влияет на способность квалифицированного читателя понимать текст. При этом авторы проходят мимо того факта, что если искаженному слову соответствует многозначный код, то для его правильного восприятия мозг интуитивно использует накопленную в регулярных чтениях информацию о частотности слов, входящих в анаграмму, и извлекает из памяти то слово, которое имеет максимальную частоту.
Литература
1. Усманов З.Д. Об упорядоченном алфавитном кодировании слов естественных языков // ДАН РТ. 2012. Т. 55. № 7. С. 545–548.
2. Марков А.А. Исчисление вероятностей. М.: ГИЗ, 1924. 589 с.
3. Гнеденко Б.В. Курс теории вероятностей. М.: Физмат- гиз, 1961. 408 с.
4. Rawlinson G.E. The significance of letter position in word recognition: PhD Thesis. Univ. of Nottingham Publ., UK, 1976.
5. MRC Cognition and Brain Sciences Unit. URL: http://www.mrc-cbu.cam.ac.uk/people/matt.davis/Cmabrigde (дата обращения: 20.02.2018).
References
- Usmanov Z.D. On the Ordered Alphabetic Coding of Natural Language Words. Reports of the Academy of Sciences of the Republic of Tajikistan. 2012, vol. 55, no 7, pp. 545–548 (in Russ.).
- Markov A.A. Calculus of Probabilities. Moscow, GIZ, 1924, 589 p.
- Gnedenko B.V. Course of the Probability Theory. Moscow, Fizmatgiz Publ., 1961, 408 p.
- Rawlinson G.E. The Significance of Letter Position in the Word Recognition: Unpublished. Univ. of Nottingham Publ., UK, 1976.
- MRC Cognition and Brain Sciences Unit. Available at: http://www.mrc-cbu.cam.ac.uk/people/matt.davis/Cmabrigde (accessed February 20, 2018).
 = “аеерртф”, а слова W = = “агент” − к той же самой цепочке CW = “агент”, поскольку в этом слове буквы уже расположены в алфавитном порядке.
= “аеерртф”, а слова W = = “агент” − к той же самой цепочке CW = “агент”, поскольку в этом слове буквы уже расположены в алфавитном порядке.
 на множестве однозначно декодируемых кодов совпадает с F–1, а на множестве многозначных кодов (образов анаграмм) каждому образу CW ставит в соответствие единственное слово W*, которое имеет максимальную частоту встречаемости в текстах в сравнении с другими словами из набора слов рассматриваемой анаграммы.
на множестве однозначно декодируемых кодов совпадает с F–1, а на множестве многозначных кодов (образов анаграмм) каждому образу CW ставит в соответствие единственное слово W*, которое имеет максимальную частоту встречаемости в текстах в сравнении с другими словами из набора слов рассматриваемой анаграммы.

 ,
,  и
и  . Как отмечалось ранее, отображения F, F(f) и F(f,l) каждому слову приписывают единственный код, однако обратные отображения в общем случае не обеспечивают однозначного декодирования. Использование отображений
. Как отмечалось ранее, отображения F, F(f) и F(f,l) каждому слову приписывают единственный код, однако обратные отображения в общем случае не обеспечивают однозначного декодирования. Использование отображений  ,
, 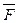 ,
,  ,
,  и
и  обладают следующими свойствами:
обладают следующими свойствами: ,
,  и
и  на кодах, однозначно декодируемых, совпадают, соответственно, с F–1, (F(f))–1, (F(f,l))–1, а на кодах анаграмм каждому из них ставят в соответствие единственное слово W*, которое имеет максимальную частоту встречаемости в текстах в сравнении с другими словами с одинаковым кодом.
на кодах, однозначно декодируемых, совпадают, соответственно, с F–1, (F(f))–1, (F(f,l))–1, а на кодах анаграмм каждому из них ставят в соответствие единственное слово W*, которое имеет максимальную частоту встречаемости в текстах в сравнении с другими словами с одинаковым кодом.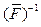 поставит в соответствие слово наказ.
поставит в соответствие слово наказ.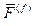 ( = F(f)), то первые два слова анаграммы получат одинаковый код каазн, а третье слово – код наазк (напомним, что при кодировании первые буквы в словах анаграмм фиксируются). Коду каазн будет сопоставляться слово казна, у которого частота больше, чем у слова казан.
( = F(f)), то первые два слова анаграммы получат одинаковый код каазн, а третье слово – код наазк (напомним, что при кодировании первые буквы в словах анаграмм фиксируются). Коду каазн будет сопоставляться слово казна, у которого частота больше, чем у слова казан. F(f) и
F(f) и  F(f,l) и
F(f,l) и  видно, что частотности многозначных кодов среди общего числа словоупотреблений равны 4,84 % и 3,75 % соответственно для эсперанто и английского языка, то есть являются относительно малыми величинами, вследствие чего читающий мозг в большинстве случаев правильно справляется с пониманием слов искаженного текста. Наряду с этим в трех других языках частотность многозначных кодов примерно на 10 % выше, поэтому ошибочность в понимании искаженных слов будет недопустимой для практического применения
видно, что частотности многозначных кодов среди общего числа словоупотреблений равны 4,84 % и 3,75 % соответственно для эсперанто и английского языка, то есть являются относительно малыми величинами, вследствие чего читающий мозг в большинстве случаев правильно справляется с пониманием слов искаженного текста. Наряду с этим в трех других языках частотность многозначных кодов примерно на 10 % выше, поэтому ошибочность в понимании искаженных слов будет недопустимой для практического применения  и
и  и не превосходят 3 % при декодировании с помощью
и не превосходят 3 % при декодировании с помощью  можно рассматривать в качестве математических моделей функционирования мозга, распознающего смысл анаграммно искаженного текста. В согласии с этим процесс понимания мозгом произвольного набора букв происходит следующим образом:
можно рассматривать в качестве математических моделей функционирования мозга, распознающего смысл анаграммно искаженного текста. В согласии с этим процесс понимания мозгом произвольного набора букв происходит следующим образом: охватывает более общую ситуацию в сравнении с
охватывает более общую ситуацию в сравнении с 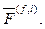 В ней нет по существу каких-либо ограничений на характер перестановок букв в слове. Вместе с тем она обеспечивает достаточно высокий уровень (не менее 97 %) распознавания смысла искаженных слов, уступая двум другим моделям в точности результата не более чем на 2 % (см. столбец 9). Если сравнивать эффективность моделей по этим двум факторам, предпочтение следовало бы отдать
В ней нет по существу каких-либо ограничений на характер перестановок букв в слове. Вместе с тем она обеспечивает достаточно высокий уровень (не менее 97 %) распознавания смысла искаженных слов, уступая двум другим моделям в точности результата не более чем на 2 % (см. столбец 9). Если сравнивать эффективность моделей по этим двум факторам, предпочтение следовало бы отдать 