Journal influence
Bookmark
Next issue
A nested model of radio-electronic systems for estimation of temporary reliability
Abstract:The effective intended application of special-purpose complexes based on radio-electronic systems involves a proper choice of optimal exploitation methods, as well as organization of maintenance, first line repair and supply of the sys- tems with replacement tools and supplies to provide high readiness of the systems for using as intended. For this purpose, there is a system of maintenance with the operating effectiveness depending on the relative position of the radio-electronic systems in a terrain. The essence of the article implies the construction of a nested model of radio-electronic systems designed to develop environment tools allowing to estimate temporary reliability characteristics of the nested radio-electronic systems as well as to undertake the study taking into account a relative position of nest elements and temporary correlation between them. The construction of the nest model has two stages. The first one is the construction of a terrain transport network representing a combination of a graph and a reachability matrix. The approach allows obtaining all possible routes between transport network elements. The second stage includes a description of radio-electronic nest systems by highlighting special type apexes in the transportation network, which include nest radio-electronic systems elements. Then there goes the construction of a spatial and temporary nested model of radio-electronic systems that represens the combination of a graph and reachability sub-matrixes with each route being relevant of temporary features (the route movement time). The spatial and temporary nested model is implemented in C#. It allows calculating temporal reliability indicators taking into account the influence of various factors and estimating the degree of their influence on the availability factor.
Аннотация:Эффективное применение комплексов специального назначения, основу которых составляют радиоэлектронные системы, предполагает выбор оптимальных методов эксплуатации, организации и проведения технического обслуживания, войскового ремонта и снабжения комплексов запасными инструментами и принадлежностями с целью обеспечения высокой степени готовности этих комплексов к применению по предназначению. Для этого создана система технической эксплуатации, эффективность функционирования которой зависит от взаимного расположения радиоэлектронных систем на местности. Основные положения работы связаны с построением модели группировки радиоэлектронных систем, которая является основой для разработки инструментальной среды, с учетом пространственного расположения элементов группировки и временных соотношений между ними. Построение модели группировки выполняется в два этапа. Первый этапа заключается в построении модели транспортной сети местности, которая представляет собой совокупность графа и матрицы достижимости. Такое представление позволяет получить все возможные маршруты между элементами транспортной сети. На втором этапе осуществляется описание группировки радиоэлектронных систем путем выделения на графе транспортной сети вершин особого типа, в которых размещаются элементы группировки радиоэлектронных систем. Далее производится построение пространственно-временной модели группировки радиоэлектронных систем, представляющей собой совокупность графа и подматриц достижимостей, где каждому маршруту между элементами группировки ставится в соответствие временной показатель (время движения по маршруту). Пространственно-временная модель группировки, программно реализованная на языке С#, позволяет рассчитать временные показатели надежности с учетом влияния различных факторов и оценить степень их влияния на коэффициент готовности.
| Authors: S.V. Ignatev (pogrebnserg@mail.ru) - Yaroslavl Higher Military College of Air Defense (Professor), Yaroslavl, Russia, Ph.D, Yu.A. Plaksa (drozhzhin-1991@mail.ru) - Yaroslavl Higher Military Air Defense College (Associate Professor), Yaroslavl, Russia, Ph.D, A.V. Krasnikov (alexalexosipov@mail.ru) - Yaroslavl Higher Military College of Air Defense (Senior Lecturer), Yaroslavl, Russia, Ph.D, А.V. Drozhin (drozhzhin-1991@mail.ru) - Yaroslavl Higher Military Air Defense College (adjunct), Yaroslavl, Russia | |
| Keywords: radio-electronic nested systems, spatio-temporal model, terrain transport network, graph, attainability matrix, temporary route system |
|
| Page views: 5846 |
PDF version article Full issue in PDF (29.03Mb) |
Актуальность поддержания сложных радиоэлектронных систем (РЭС) на заданном уровне надежности не вызывает сомнений. Для этого создана система технической эксплуатации (СТЭ), которая, в свою очередь, включает системы технического обслуживания, диагностирования и материально-технического обеспечения [1]. Функционирование первых двух систем направлено на увеличение времени наработки РЭС до отказа (TO) и уменьшение их времени восстановления (TВ) соответственно. На сегодняшний день исследования ведутся по каждой системе, причем в разных направлениях [2–6]. В основу таких исследований положены математические модели, учитывающие влияние различных параметров этих систем на надежность РЭС. Кроме того, они проводились при определенных ограничениях, одним из которых является допущение того, что РЭС полностью укомплектованы требуемыми материально-техническими ресурсами (МТР) и последние не оказывают никакого воздействия на TO и TВ. Такой подход не позволяет в полной мере оценить эффективность функционирования СТЭ при обеспечении заданного уровня надежности группировки РЭС, что приводит к необходимости более глубокого исследования процесса восстановления РЭС. Опыт эксплуатации показывает, что эффективность функционирования СТЭ будет зависеть от ряда факторов. Прежде всего это взаимное расположение на местности элементов группировки РЭС, что определяет пространственную топологию группировки (так называемый пространственный параметр). Кроме того, в процессе эксплуатации возникает ряд задач [7]: доставка запасных частей, инструментов и принадлежностей, горюче-смазочных материалов, прибытие специалиста для ремонта и т.д. Их решение характеризуется временными показателями, которые, в свою очередь, являются составляющими времени восстановления: ТВ=tк + tр + tподг.+ tпер. + tдост. + tадм., где tк – время поиска и локализации отказавшего элемента; tр – время устранения отказа; tподг. – время подготовки к включению; tпер. – время перерывов обслуживающего персонала; tдост. – время доставки исправного элемента; tадм. – время прибытия специалиста для ремонта [1]. Как правило, решение последних двух задач осуществляется с использованием транспортной сети местности (ТСМ), на которой расположена группировка РЭС. Учитывая это, время восстановления элемента группировки можно представить как ТВ = ТЭГ + ТТС, где ТЭГ = tк + tр + tподг. + tпер. – время выполнения операций в элементе группировки; ТТС = tдост. + + tадм. – время выполнения операций с использованием транспортной сети (ТС). В этом случае расстояние s между узлами ТСМ, в которых размещаются элементы группировки РЭС, и средняя скорость движения v будут определять ТТС (так называемый временной параметр). Для комплексного учета возможных ситуаций и проведения дальнейших исследований с оценкой показателей надежности, связанных с временными параметрами (коэффициент готовности, коэффициент технического использования, время восстановления), необходимо построить модель группировки РЭС, учитывающую пространственное положение ее элементов и временные соотношения между ними, которую будем называть пространственно-временной моделью группировки РЭС. С учетом того, что группировка РЭС располагается на местности (на ТС), построение данной модели целесообразно осуществить в два этапа. Первый этап предполагает построение модели ТСМ, на которой размещается группировка РЭС. На втором этапе производится описание группировки РЭС на модели ТСМ путем размещения в ее узлах элементов группировки. Первый этап (построение модели ТСМ) Рассмотрим абстрактный пример. Пусть имеется некая ТСМ, на которой размещается группировка РЭС (рис. 1). Для ее формализации осуществим переход от концептуальной модели (разнотипных элементов, описанных в терминах предметной области) к ее математическому описанию (формальным однотипным). Очевидно, что наиболее просто это осуществимо с использованием теории графов [8]. Представим узловые пункты ТС (населенные пункты, элементы РЭС, пункты перегрузки груза и смены транспорта, развилки дорог и т.д.) вершинами (узлами) графа, а пути сообщения между этими пунктами (наземные, воздушные, водные) – ребрами графа. В результате получим мультиграф ТС (рис. 2): GП = , где U = {ui ½ i = 1, 2, …, 5} – множество вершин графа; R = {rk ½ k = 1, 2, …, 8} – множество ребер графа [4]. В общем случае GП = , где U = {ui ½ i = 1, 2, …, I}, I – количество вершин графа; R = {rk ½ k = 1, 2, …, K}, K – количество ребер графа. Каждая вершина графа GM (рис. 3) нагружается кортежем ei = [ti, ci], (1) где ti – время выполнения определенных действий (время задержки) в i-м узле ТС (например: дозаправка транспортного средства (ТСр), оформление необходимых документов, перегрузка материальных ресурсов из одного ТСр в другое и т.д.), которые необходимо выполнить, чтобы продолжить дальнейшее движение; ci – стоимость выполнения этих действий в i-м узле ТС. Ребра графа GM нагружены кортежем
где rk – обозначение участка пути ТС (ребра графа); sk – протяженность участка пути ТС; qn – тип ТСр, движущегося по участку пути ТС; vk(qn) – скорость ТСр, движущегося по участку пути ТС; gk – коэффициент изменения скорости ТСр; ck(qn) – стоимость перевозки конкретным типом ТСр за единицу пути. Исходя из вышеизложенного, в общем виде граф маршрутов ТС [8, 9] опишется выражением
Веса вершин и ребер графа (рис. 3) могут выступать в качестве их идентификаторов. Поэтому GМ опишем матрицей смежности взвешенного графа [9–11] (весовой матрицей смежности) S(GМ) = [sij]IxI вида
В результате весовая матрица смежности S(GМ) для рассматриваемого графа будет иметь следующий вид:
Для получения возможных маршрутов между i-й и j-й вершинами графа GМ – mij, где
где d(G) – диаметр графа GМ. При этом операцию умножения при возведении матрицы смежности в степень необходимо рассматривать как конкатенацию, а операцию сложения – как дизъюнкцию и учитывать только простые маршруты, в которых отсутствуют повторения вершин графа между начальным ei и конечным ej узлами маршрута: ei ¹ … ¹ eq ¹ … ej, то есть каждая вершина в одном маршруте должна встречаться один раз. В общем виде
Так, например, в соответствии с выражением (7) маршруты между узлами e1 и e2 опишутся следующим выражением:
Тогда с учетом примера (8) представим матрицу достижимости:
Содержимое ячеек матрицы (9) полностью определяет систему маршрутов ТС [4, 9]. В общем виде модель ТС запишется как
В соответствии с выражением (10) количество маршрутов между начальным ei и конечным ej узлами ТС Hij будет равно количеству слагаемых по операции дизъюнкции. Второй этап (описание группировки РЭС на ТСМ) Для описания группировки РЭС выделим из рассматриваемого графа ТС вершины особого типа, в которых размещаются элементы группировки РЭС, и объединим их в множество E¢: E¢ Í E. Пусть для рассматриваемого графа ТС (рис. 2) это вершины e1, e4, e5: E¢ = e1, e4, e5. В результате получим граф группировки РЭС (рис. 4). Особенностью данных вершин является то, что попарное сочетание вершин множества образуют начало и конец маршрутов ТС. Другие вершины графа (рис. 4) не могут выступать в качестве начала и окончания маршрутов. Матрица достижимости D¢(GM) для вершин графа из множества E¢ получается из D(GM) путем вычисления соответствующих строк и столбцов:
Следует отметить, что полученная подматрица является симметричной. Учтем сделанные ранее замечания (вес вершины (ребра) при движении в прямом и обратном направлениях одинаковый). Для уменьшения количества вычислений будем ис- пользовать только те ячейки преобразованной матрицы достижимости, которые находятся выше (ниже) главной диагонали. Тогда система маршрутов между элементами группировки для рассматриваемого примера примет вид
Для дальнейшего решения задачи преобразо- ванную матрицу достижимости представим в виде набора подматриц достижимостей, в ячейках которых между вершинами ei и ej записывается только один h-й маршрут
Из выражения (12) видно, что между вершинами e1 и e4 существуют 13 маршрутов, то есть H1,4 = 13. Аналогично H1,5 = 11, H4,5 = 17 В общем виде выражение для определения всех маршрутов между элементами группировки представим в виде
Учитывая, что в одной ячейке подматрицы достижимости записывается один маршрут и выбор маршрута является (может быть) произвольным (осуществляется в произвольном порядке), количество подматриц достижимости D¢(GM) для рассматриваемого примера определяется как число сочетаний из общего количества маршрутов по количеству элементов группировки: и в общем виде представлено как
где e¢ – количество вершин особого типа (элементов группировки). Для рассматриваемого примера набор подматриц достижимости представим в матричной форме:
или в виде системы
Для каждого h-го маршрута системы рассчитывается ТТС. Необходимые данные для этого содержатся в весах графа e и p. Время движения на n-м типе ТС qn на k-м участке маршрута будет определяться как Тогда общее время выполнения операций на всем маршруте ТС найдем как сумму соответствующих величин исходя из количества участков на этом маршруте и количества узлов, входящих в этот маршрут. Например, для маршрута m1 между вершинами e1 и e4 (см. (13)) получим следующее значение времени ТТС:
Учитывая описание маршрута выражением (20), систему маршрутов на примере выражения (12) можно представить временной системой маршрутов:
В общем виде ТТС между вершинами ei и ej на h-м маршруте запишется как
В итоге получим пространственно-временную модель группировки РЭС H, представляющую собой совокупность графа (3) и подматриц достижимостей (19), где каждому h-му маршруту между вершинами ei и ej ставится в соответствие время ТТС на этом маршруте. В общем виде пространственно-временная модель группировки РЭС запишется как H = GM, D²z(GM), где
Модель программно реализована на языке программирования С# (получены свид. о рег. прогр. для ЭВМ № 2015661720 и № 2017616840). Интерфейс представлен на рисунках (см. рис. 5 и http:// www.swsys.ru/uploaded/image/2018-3/2018-3-dop/ 13.jpg, http://www.swsys.ru/uploaded/image/2018-3/2018-3-dop/14.jpg, http://www.swsys.ru/uploaded/ image/2018-3/2018-3-dop/15.jpg). Использование данного программного продукта позволяет рассчитывать временные показатели надежности группировки РЭС и проводить ис- следования с учетом влияния на них следующих факторов: расположение элементов группировки на местности, расстояние между элементами группировки, тип используемого транспорта, скорость движения, условия, в которых осуществляется движение, время выполнения работ. Литература 1. Анисимов О.В., Беляков Р.А., Игнатьев С.В., Каменский И.Е., Мещеряков В.Д., Приступюк А.И., Тихонов В.Б., Черваков В.О. Основы эксплуатации радиотехнических систем. Ярославль: Изд-во Филиала ВКА им. А.Ф. Можайского, 2015. 200 с. 2. Давыдов П.С. Техническая диагностика радиоэлектронных систем. М.: Радио и связь, 1988. 256 с. 3. Дорохов А.Н., Керножицкий В.А., Миронов А.Н., Шестопалова О.Л. Обеспечение надежности сложных технических систем. СПб: Лань, 2016. 352 с. 4. Анисимов О.В., Осипов А.А., Харитонов А.В., Беля- ков Р.А. Техническое обслуживание зенитного ракетного вооружения в системе ВКО // Вестн. ВУНЦ ВВС. 2012. Вып. 15. Ч. 1. С. 34–38. 5. Анисимов О.В., Попов Т.А. Метод информационной поддержки процесса диагностирования сложных технических комплексов на основе паттернов элементов электрических схем радиоэлектронной аппаратуры // Теоретические и прикладные проблемы развития и совершенствования автоматизированных систем управления военного назначения: сб. тез. II Всерос. науч.-технич. конф. СПб: 2015. С. 16–17. 6. Анисимов О.В., Курчидис В.А., Приветень А.С. Дескриптивная модель радиоэлектронной аппаратуры на основе онтологий для автоматизации информационной поддержки обслуживающего персонала при диагностировании сложных технических комплексов // Наукоемкие технологии в космических исследованиях Земли. 2016. Т. 8. № 3. С. 72–77. 7. Медведев В.М., Мищенко В.И., Солоха Н.Г. Развитие концепции эксплуатации изделий // Вестн. ОГУ. 2008. № 85. С. 149–157. 8. Черкесов Г.Н. Оценка надежности систем с учетом ЗИП. СПб: БХВ-Петербург, 2012. 480 с. 9. Игнатьев С.В., Тихонов В.Б., Красников А.В., Оси- пов А.А. Пространственно-временная модель транспортной сети системы материально-технического обеспечения эксплуатации группировки радиоэлектронных средств // Программные продукты и системы. 2017. № 3. С. 510–517. 10. Оре О. Теория графов. М.: Наука, 1980. 336 с. 11. Горбатов В.А., Горбатов А.В., Горбатова М.В. Дискретная математика. М.: Астрель, 2003. 447 с. 12. Кристофидес Н. Теория графов. Алгоритмический подход. М.: Мир, 1978. 432 с. References
|
| Permanent link: http://swsys.ru/index.php?id=4505&lang=en&page=article |
Print version Full issue in PDF (29.03Mb) |
| The article was published in issue no. № 3, 2018 [ pp. 598-604 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Пространственно-временная модель транспортной сети системы материально-технического обеспечения эксплуатации группировки радиоэлектронных средств
- Фазовый переход наработки на отказ в растущих вычислительных сетях
- Технологические процессы с гибкими связями типа «звезда» для интерактивных программных систем
- Интеллектуальный подход к автоматизации технологических и производственных процессов
- Алгоритмы навигации на внешней поверхности модели международной космической станции
Back to the list of articles



 , (2)
, (2) (3)
(3) (4)
(4) (5)
(5)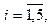
 и i ¹ j, находится матрица достижимости:
и i ¹ j, находится матрица достижимости: (6)
(6) (7)
(7) (8)
(8) . (9)
. (9) (10)
(10)

 (12)
(12) (13)
(13)
 , где h − номер маршрута в системе mij. Например, для рассматриваемого примера одна из набора подматриц достижимости будет иметь вид
, где h − номер маршрута в системе mij. Например, для рассматриваемого примера одна из набора подматриц достижимости будет иметь вид (GM)=
(GM)=


 Тогда общее количество маршрутов между элементами группировки может быть вычислено как H = H1,5 + + H4,5 = 41.
Тогда общее количество маршрутов между элементами группировки может быть вычислено как H = H1,5 + + H4,5 = 41. . (16)
. (16)
 (17)
(17)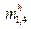


 (19)
(19) , а время задержки в i-м узле маршрута – временем ti.
, а время задержки в i-м узле маршрута – временем ti. . (20)
. (20) (21)
(21) . (22)
. (22)
 (23)
(23)
