Software & Systems

Nowadays, the ArcGIS software is the most well-known product of the ESRI (Environmental Systems Research Institute) used by millions of GIS users all over the world. This software is a set of representative software tools for collecting, organizing, managing, analyzing, sharing and distributing geographical information [1]. ArcGIS is a leading platform for building and using GIS. Therefore, specialists (scientists and engineers) around the world use it to apply geographic knowledge in government, business, science, education and mass media. The ArcGIS software includes four units (components implementing individual applications): ArcMap; ArcCatalog; ArcScene; ArcGlobe. ArcMap and ArcCatalog allow using a wide range of data sources. It is possible to view this data and organize them in ArcCatalog, to create metadata and manage them, to search for data sources by their content. ArcMap allows creating map layers based on these sources. The ArcGlobe component is a part of the ArcGIS 3D-Analyst extension module. This application is designed to work with large data sets and visualize raster and vector data [2]. The ArcScene component is a 3D image viewer and is suitable for navigation and work with 3D vector and raster data. Based on OpenGL technology, ArcScene supports complex three-dimensional linear symbols, provides texture mapping, surface creation, and TIN (Triangulated Irregular Network) mapping.

The ArcScene component allows combining multiple data layers in 3D environment. To locate 3D objects, the application uses height data derived from its geometry, object attributes, layer properties, or a specified 3D surface. Each layer of a 3D image can be processed separately from others. Data with different spatial reference are reprojected or displayed using only relative coordinates (relative to each other in a local or proposed coordinate system).

The ArcScene application is fully integrated into the geoprocessing environment, therefore it possible to use numerous analytical tools and functions to analyze and pre- sent data. The program also provides many tools for edit- ing and manipulating 3D raster and vector data.

ArcScene makes it possible to project any layer on another. In the example in Figure 1, a layer of buildings is projected on the layer of a digital elevation model. 3D buildings and a digital elevation model (DEM) after projecting these buildings on DEM are shown in figure (refer to http://www.swsys.ru/uploaded/image/2019-1/2019-1-dop/18.jpg).

The most important things related to cartography are cartographic projections. When transiting from the earth’s physical surface to its mapping into a plane (on a map), there are two operations. The first one is projecting the earth's surface with its complex relief to the surface of the earth's ellipsoid with the dimensions determined by geodetic and astronomical measurements. The second is projecting the earth's ellipsoid on a surface using one of cartographic projections.

All cartographic projections are classified according to a number of features including the nature of distortions (equal-angle, equal-size, equidistant and arbitrary), the construction method (cylindrical, conical, azimuthal, and multi-faceted projections), the pole position of the normal coordinate system (straight lines or normal, transverse or equatorial, transverse or equatorial, oblique or horizontal), etc. [3].

Now we are going to discuss the first difficulty in ArcScene that arises when adding 3D data (raster or vector) such as a point, a line, a polygon, or DEM in ArcScene. These objects or data are displayed as vertical lines. The difficulty is that the data is in a geographic projection. Therefore the coordinates of points in the X and Y planes are measured in degrees (longitude and latitude) and have small values, while the units of point heights are measured in meters, and ArcScene assumes that the horizontal coordinated (X, Y) and the vertical coordinate (Z) have the same units. This leads to the fact that the vertical units will be stretched largely. Therefore, it is necessary to ensure a correspondence between horizontal and vertical coordi- nate units. The example of such case is presented in figure (refer to http://www.swsys.ru/uploaded/image/2019-1/ 2019-1-dop/18.jpg). DEM in ArcScene is a vertical line after displaying it in three dimensions.

The heights of the points in figure (refer to http://www. swsys.ru/uploaded/image/2019-1/2019-1-dop/18.jpg) in relation to the values of the X and Y coordinates are very large, so the 3D model is displayed as a vertical line.

There are several solutions for this problem.

The first one is to project data (raster or vector layer) on a non-geographic projection (metric projection) in order to create a correspondence between horizontal (X and Y) and vertical (Z) layers to make them all in metric units. For raster layers, it is necessary to follow the steps.

1.    Start ArcToolbox.

2.    Click Data Management Tools > Projections and Transformations > Raster > Project Raster tool.

3.    Specify the required parameters.

4.    Select a metric projection (for example, UTM).

5.    Run the tool.

For vector data, the steps are the following.

1.    Start ArcToolbox.

2.    Click Data Management Tools > Projections and Transformations > Feature > Project.

3.    Specify the required parameters.

4.    Select a metric projection (for example, UTM).

5.    Specify the transformation if necessary.

6.    Run the tool.

The second option is to edit the unit of height coordinate (Z) for a layer (raster or vector) with a very small value. This requires doing the follow steps.

1.    Right-click the layer in the table of contents and select properties.

2.    Click on the “Base heights” tab.

3.    Adjust the value to a number between 0.001 and 0.0001 (http://www.swsys.ru/uploaded/image/2019-1/ 2019-1-dop/19.jpg).

This solution is to reduce the vertical scale (Z) in order to eliminate the distortion caused by big height values.

The third option is to adjust the vertical exaggeration of the entire scene to a very small value. It includes the following steps.

1.    Click View > Scene Properties.

2.    Click the “General” tab.

3.    Adjust the vertical exaggeration to a value from 0.001 to 0.0001 (http://www.swsys.ru/uploaded/image/ 2019-1/2019-1-dop/20.jpg).

In fact, this solution is similar to the second one. It only differs in changing a vertical scale not only for a certain layer with the problem, but for the whole setting, that displays all data layers.

After applying one of the three above solutions, the DEM is displayed as shown in Figure 2.

It can be noticed that Figure 2 displays DEM in 3D, so now it actually represents the terrain and we can visualize and measure the height and coordinates of any point without any problems.

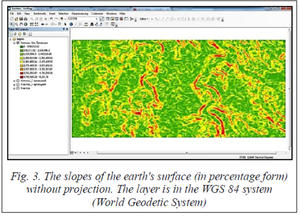
In order to explain this problem related to coordinate systems in general, we will give another example of a similar difficulty in ArcMap. We input a digital elevation model in the form of a raster data layer in ArcMap, so that we can extract the slopes of the earth's surface (in the form of raster data) as a degree or a percentage. In this case, we have DEM downloaded from the site of the US Geological Survey [4] with the accuracy (30´30 m). The data in this site is in the geographical coordinate system (World Geo- detic System WGS 84). According to this projection, the position of each point on the earth's surface is determined by the latitude and longitude (degrees).

In ArcMap, we extracted the slopes vales of the earth's surface depending on DEM that are shown in Figure 3. But as shown in the figure (refer to http://www.swsys.ru/uploaded/image/2019-1/2019-1-dop/21.jpg), the values are huge and illogical. This can be explained by the fact that in the layer of slopes, the X and Y values (the distance between points on the map) are determined by latitude and longitude in degrees (i.e. angular, non-metric system), while the height of a point is determined by metric units. Thus, the incompatibility between the values creates a problem with illogical and huge slope values.

The slope between the two considered points can be defined as a ratio of the vertical distance between two points to the horizontal distance between them. Figure 4 shows the principle and the mathematical concept of a slope. In this case, the horizontal distance between points is measured in degrees, therefore its magnitude will be very small since 1 degree here equals almost 111 km. In these calculations, we assume that the Earth is a sphere with a radius of 6370 km, therefore, the diameter will be almost 40023 km, so 1 degree is 40023/360 = 111.177 km.

If a distance between two points is 30 m, then in degrees it will be equal to 0.00027778 (30/111000 = 0.00027778 degrees or 1 second). If the difference between the heights of these points is 2 meters, then the slope will be the following:

Slope = Tangent = 2 / 0.00027778 = 7200 = 720000 %.

In this case, we have illogical values. To avoid this problem and obtain the correct and logical values, it is necessary to put the DEM layer (raster) in the metric coordinate system. For this purpose, we have chosen a Mercator universal transverse projection, or UTM (Universal Transverse Mercator). In this projection, the Earth is divided into 60 six-degree zones (6° x 60 = 360°). The zones are numbered from 1 to 60 from 180°W. Each zone has its own central meridian. The UTM projection is based on a cylinder that is parallel to the equator, so it is transverse. UTM coordinates are measured in meters. The X-axis (east direction) starts from the central meridian of the zone. The Y-axis (north direction) starts from the equator. To exclude negative coordinates, the projection changes the values at the origin. The magnitude of the shift from the central meridian is a false eastern shift, it is equal to 500,000 meters; the shift from the equator is a false north shift (0 meters) [5].

The UTM projection is conformal, i.e. it keeps the form in exact observance of small forms and the minimum dis- tortions of large forms within a zone. A direction is also preserved within certain limits. There is a slight area dis- tortion. The scale is constant along the central meridian with a scale factor of 0.9996 in order to reduce latitudinal distortions within each zone [6].

In the ArcMap, it is possible to choose an appropriate projection and edit its parameters depending on the studied area. Therefore, using this option for the studied area with a longitude varying from 37.49–37.56, we have created a new Mercator projection with the central meridian (37.525) in order to reduce distortions. At the end, we have obtained the correct values of earth's surface slopes for the same studied area (Fig. 5).

Obviously, after solving the presented problem, we got logical and corrected values of the earth's surface slopes as shown in figure (refer to http://www.swsys.ru/uploaded/image/2019-1/2019-1-dop/22.jpg). They vary from zero to 80.44 %.

Conclusion. Based on the foregoing, we can conclude that GIS is not an independent system or just simple software that might be used independently. On the contrary, a GIS user has to possess the basic knowledge of a number of GIS related sciences, primarily the earth sciences like geodesy and cartography. The lack of basic knowledge about these sciences might lead to incomprehensible, inaccurate or incorrect results, which are very difficult to correct in most cases. This paper shows the necessity to ensure compatibility between displayed data regardless of their type (raster or vector). Therefore, it is necessary to check coordinate systems, processed data layers and unit systems used in the program by default. Sometimes they do not meet the requirements and lead to incomprehensible results.

References

1.     About 3D Navigation Tools in ArcScene. Available at: http://desktop.arcgis.com/en/arcmap/latest/extensions/3d-analyst/3d-navigation-tools-in-arcscene.htm/ (accessed October 12, 2018).

2.     Kennedy H. Data in three dimensions: a guide to ArcGIS 3D analyst. Delmar Cengage Learning, 2004, 256 p.

3.     Berlyant A.M. Cartography. Moscow, Aspekt Press, 2002, 336 p.

4.     EarthExplorer. Available at: https://earthexplorer.usgs.gov/ (accessed October 12, 2018).

5.     ESRI. ArcGIS 9 Map Projections. 2004, 165 p.

6.     Zhmoydyak R.A., Atoyan L.V. Cartography. Lecture course. Minsk, 2006, 192 p.

7.     Kennedy H. Introduction to 3D Data: Modeling with ArcGIS 3D Analyst and Google Earth. John Wiley & Sons Publ., 2010, 350 p.

8.     ArcGIS 3D Analyst. 124 p. 

9.     Topchilov M.A., Romashova L.A., Nikolaeva O.N. Cartography. Novosibirsk, 2009, 110 p.

10.  Seredovich V.A., Klyushnichenko V.N., Timofeeva N.V. Geographic Information Systems (Purpose, Functions, Classification). Novosibirsk, 2008, 117 p.

Литература

1. About 3D Navigation Tools in ArcScene. URL: http://desktop.arcgis.com/en/arcmap/latest/extensions/3d-analyst/3dnavigation-tools-in-arcscene.htm/ (дата обращения: 12.10.2018).
2. Kennedy H. Data in three dimensions: a guide to ArcGIS 3D analyst. Delmar Cengage Learning, 2004, 256 p.
3. Берлянт А.М. Картография. М.: Аспект Пресс, 2002. 336 с.
4. EarthExplorer. URL: https://earthexplorer.usgs.gov/ (дата обращения: 12.10.2018).
5. ArcGIS 9 Картографические проекции; [пер. с англ.]. М.: DATA+, 2004. 109 c.
6. Жмойдяк Р.А., Атоян Л.В. Картография. Минск, 2006. 192 c.
7. Kennedy H. Introduction to 3D data: Modeling with ArcGIS 3D analyst and google earth. John Wiley & Sons, 2010, 350 p.
8. ArcGIS 3D Analyst. URL: https://docplayer.ru/31710826-Arcgis-3d-analyst-uchebnoe-posobie.html (дата обращения: 12.10.2018).
9. Топчилов М.А., Ромашова Л.А., Николаева О.Н. Картография. Н.: Изд-во СГГА, 2009. 110 c.
10. Середович В.А., Клюшниченко В.Н., Тимофеева Н.В. Геоинформационные системы (назначение, функции, классификация). Н.: Изд-во СГГА, 2008. 117 c.