Software & Systems

При построении математического описания химико-технологических процессов требуется определение динамики взаимодействующих веществ химических реакций. Одним из этапов математической обработки экспериментальных данных является построение и исследование кинетической модели химической реакции, которая представляет собой систему обыкновенных дифференциальных уравнений. Обратная кинетическая задача заключается в определении вида кинетической модели реакции и ее параметров на основе экспериментальных данных [1]. В процессе поиска кинетических параметров химической реакции необходимо минимизировать функционал отклонения экспериментальных данных от расчетных значений, то есть решить оптимизационную задачу.

Однако большинство методов оптимизации, применяемых для решения обратной за- дачи, зависит от начального приближения поиска решения [2–4]. Одним из методов, позволяющих отыскать глобальный оптимум независимо от начальной точки поиска, является метод дифференциальной эволюции. Это прямой метод оптимизации, так как в ходе его работы не требуется нахождение производных целевой функции, а необходимо определять значения только целевой функции [5, 6].

Расчет кинетических параметров химической реакции является трудоемким процессом, поскольку для вычисления значений целевой функции необходимо неоднократно решать систему дифференциальных уравнений, то есть прямую кинетическую задачу. В связи с этим возникает необходимость в создании программного средства, позволяющего автоматизировать все этапы решения обратной кинетической задачи, что существенно сократит вы- числительные затраты исследователя при составлении математического описания химических процессов.

Алгоритм поиска кинетических параметров реакции

Пусть кинетическая модель химической реакции описывается системой дифференциальных уравнений:

 i = 1, …, n,                         (1)

где x = (x1, x2, …, xn) – вектор концентраций веществ, вид функции f определяется схемой реакции; k = (k1, k2, …, km) – вектор констант скоростей стадий, причем константа скорости j-й стадии определяется из уравнения Аррениуса:

           (2)

где k0j – предэкспоненциальный множитель; Ej – значение энергии активации j-й стадии; T – температура; R – универсальная газовая постоянная [7].

Неизвестными параметрами кинетической модели реакции являются вектор значений предэкспоненциальных множителей k0 = (k01, k02, …, k0m) и вектор значений энергий активации E = (E1, E2, …, Em) стадий реакции.

Требуется найти такой набор значений кинетических параметров k0 и E, при которых функционал отклонения между расчетными и экспериментальными данными принимает минимальное значение:

                            (3)

где  – значения концентраций веществ, полученных в результате решения системы дифференциальных уравнений (1);  – экспериментальные значения концентраций веществ; k – количество точек эксперимента; n – количество веществ.

Сформулируем алгоритм поиска кинетических констант с помощью метода дифференциальной эволюции. Данный метод имитирует этапы эволюции живых организмов [8, 9]. Аналогом поколений живых существ выступает набор векторов с фиксированным числом координат kj = (kj1, kj2, …, kjm), j = 1, …, count_Pop (count_Pop задает количество векторов в популяции), которые представляют собой кинетические константы скоростей реакции. Представим алгоритм в виде последовательности шагов.

Шаг 1. Создание начальной популяции.

Задаются параметры алгоритма: размер популяции count_Pop, максимальное количество популяций max_Pop, весовой масштабирующий множитель F Î [0.4, 1], параметр оператора скрещивания Cross Î [0, 1], счетчик итераций i = 0.

Случайным образом генерируется начальная популяция констант скоростей стадий k1, k2, …, kcount_Pop, где kj = (kj1, kj2, …, kjm), j = 1, …, count_Pop, в пределах пространства поиска.

Устанавливается номер вектора-мишени mish = 1, и вектору-мишени kmish присваивается значение первой константы скорости k1.

Для каждого набора кинетических констант вычисляется значение целевой функции (3) путем решения системы дифференциальных уравнений (1).

Шаг 2. Мутация.

Из текущей популяции случайным образом выбираются два вектора kq, kp так, что q ¹ mish, p ¹ mish, и третий вектор kl (l ¹ mish) с наименьшим значением целевой функции (3). Генерируется новый вектор-мутант по формуле kmut = = kl + F(kq – kp).

Шаг 3. Кроссовер.

Создается пробный вектор kprob следующим образом. Для каждой координаты вектора kj = = (kj1, kj2, …, kjm), j = 1, …, count_Pop, на интервале [0, 1] генерируется случайное число ri (i = 1, …, m). Если сгенерированное число меньше значения параметра оператора скрещивания (ri £ Cross), то kprob i := kmut i, иначе kprob i := := kmish i. Для пробного вектора kprob и вектора-мишени kmish вычисляются значения целевой функции (3).

Шаг 4. Создание новой популяции.

Если Q(kprob) < Q(kmish), то в новую популяцию помещается пробный вектор, иначе – вектор-мишень.

Осуществляется переход к следующей итерации работы алгоритма. Если mish < count_ Pop, то mish := mish + 1 и выполняется переход на шаг 2, иначе – на шаг 5.

Шаг 5. Проверка условия окончания поиска.

Если i < max_Pop, то i := i + 1 и осуществляется переход к шагу 2, иначе – к шагу 6.

Шаг 6. Формирование решения задачи поиска кинетических констант.

Из последней популяции k1, k2, …, kcount_Pop  выбирается вектор констант, который соответствует наименьшему значению целевой функции. Этот вектор будет решением задачи поиска кинетических констант стадий реакции.

На основе вычисленных значений констант скоростей стадий реакции определяются вектор значений предэкспоненциальных множителей k0 = (k01, k02, …, k0m) и вектор значений энергий активации E = (E1, E2, …, Em) стадий реакции.

Из уравнения Аррениуса (2) рассчитываются значения энергий активации:

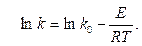
Если известны значения кинетических констант скоростей стадий реакции при различных значениях температуры ki(T1), ki(T2),  …, ki(TNT), i = 1, …, m, то получаем систему уравнений:

                        (4)

Обозначим   

  j = 1, …, NT.

Тогда система уравнений (4) примет вид

Неизвестными параметрами данной системы уравнений являются a и b, для вычисления которых методом наименьших квадратов требуется минимизировать функционал:

                    (5)

Значения энергий активаций E и константы k0 рассчитываются по формулам:

k0 = ea, E = – bR.                                    (6)

Сформулированный алгоритм программно реализован на языке программирования Delphi. Разработанное приложение позволяет по набору экспериментальных данных вычислять кинетические параметры химических реакций.

Описание ПО

Работа программы состоит из нескольких этапов.

Этап 1. Считывание из файла схемы реак- ции.

С помощью пункта меню «Файл» из текстового файла считывается схема реакции в специальном формате, который включает в себя обозначения реагентов и продуктов реакции. Например, реакция вида X1 + X2 ® X3 должна быть представлена в файле в виде строки: X1 + X2 ® X3.

Синтаксический анализатор программы на основе схемы реакции выстраивает кинетическую модель, то есть систему обыкновенных дифференциальных уравнений.

Этап 2. Считывание/ввод экспериментальных данных.

Для расчета значения функционала отклонения между расчетными и экспериментальными данными необходимо ввести/считать из файла значения концентраций веществ, полученные опытным путем. Это можно сделать на вкладке «Экспериментальные данные» (рис. 1) либо непосредственно введя в таблицу значения концентраций реагентов, либо открыв данные из текстового файла («Считать из файла»), причем первый столбец значений означает текущее время, остальные – текущие значения концентраций веществ.

Этап 3. Ввод параметров процесса.

В ходе решения оптимизационной задачи многократно решается построенная система дифференциальных уравнений, поэтому пользователю необходимо ввести на вкладке «Параметры процесса» значения начальных концентраций веществ, температуру и время протекания реакции.

Этап 4. Установка параметров алгоритма.

На вкладке «Параметры алгоритма» необходимо ввести такие параметры, как размер популяции, количество популяций, количество констант скоростей стадий, ограничения на константы скоростей реакции, весовой масштабирующий множитель (число из интервала [0.4, 1]), параметр оператора скрещивания (число из интервала [0.4, 1]).

После установки необходимых параметров нужно нажать на кнопку «Расчет k». В результате вычислений определяются значения кинетических констант реакции. Чтобы рассчитать значения предэкспоненциальных множителей и энергий активации стадий, необходимо перейти на вкладку «Кинетические параметры» и нажать на кнопку «Расчет k0 и E». На основе найденных кинетических параметров решается прямая кинетическая задача, решение ее представляется в численном и графическом видах (вкладки «Решение прямой задачи», «Графики»). На вкладке «Графики» строится график динамики концентраций веществ, рассчитанных по вычисленным кинетическим параметрам и найденных экспериментальным путем. Пользователь может отобразить концентрации всех веществ или части из них. Кроме этого, для каждого вещества вычисляется относительная погрешность значений концентраций, что дает возможность сделать вывод об удовлетворительном согласовании опытных данных с рассчитанными значениями.

Вычислительный эксперимент

Применяя разработанное программное средство, вычислим кинетические параметры реакции получения фталевого ангидрида.

Фталевый ангидрид – один из важнейших видов сырья для производства лакокрасочных материалов, пластификаторов, лекарственных веществ, красителей, присадок к смазочным маслам, ускорителей вулканизации каучука, добавок к реактивным топливам, инсектицидов.

Реакция получения фталевого ангидрида представляется совокупностью следующих стадий [10]:

X1 ® X2

X2 ® X4

X1 ® X3                                                  (7)

X1 ® X4

X2 ® X3

X3 ® X5,

где X1 – нафталин; X2 – нафтохинон; X3 – фта- левый ангидрид; X4 – углекислый газ; X5 – малеиновый ангидрид.

Кинетическая модель данной реакции представляет собой систему дифференциальных уравнений:

                          (8)

где xi – концентрация i-го вещества (i = 1, …, 5) (моль/л); kj – константа скорости j-й стадии реакции (j = 1, …, 6) (1/ч).

На основании экспериментальных данных, представленных в [10], для реакции получения фталевого ангидрида рассчитаны значения кинетических констант и энергии активации (рис. 2).

В ходе работы алгоритма система дифференциальных уравнений (8) с начальными условиями решалась методом прогноза и коррекции. Вычисления проводились при следующих параметрах оптимизационного алгоритма: размер популяции – 60, количество популя- ций – 2 000, количество констант скоростей стадий – 6, весовой масштабирующий множитель – 0.6, параметр оператора скрещивания – 0.7. Начальные концентрации веществ задавались следующими значениями (моль/л): x1(0) = 1, xi(0) = 0, i = 2, …, 5.

Время протекания реакции – 0.6 ч.

На рисунке 2 приведены численные значения кинетических констант и энергий активации стадий реакции, а также представлены графики динамики концентраций веществ Х1 и X2, вычисленных на основе найденных кинетических параметров и полученных экспериментальным путем при температуре 620 °К.

Заключение

Чтобы определить, согласуются ли экспериментальные данные с рассчитанными значениями концентраций, в программе для каждого вещества рассматриваемой реакции (7) вычислены относительные погрешности нахождения значений концентраций веществ: d(X1) = = 11,5 %, d(X2) = 8,5 %, d(X4) = 9 %, d(X5) = = 11,2 %.

Поскольку отклонение расчетных значений концентраций, полученных на основе вычисленных кинетических параметров, от опытных данных не превышает 12 %, можно сделать вывод об удовлетворительном согласовании с результатом эксперимента.

Таким образом, разработанная программа позволяет рассчитать значения констант скоростей и энергий активации ее стадий. Кинетиче- ская модель реакции, построенная на основе вычисленных кинетических параметров, доста- точно близко описывает динамику концентраций веществ, полученных экспериментальным путем.

Программное средство может применяться в практической деятельности научно-исследовательских лабораторий промышленных предприятий при проведении вычислительных экспериментов разрабатываемых процессов, а также при разработке их математического обеспечения.

Исследование выполнено при финансовой поддержке РФФИ и Правительства Республики Башкортостан в рамках научного проекта № 17-47-020068.

Литература

1.    Губайдуллин И.М., Рябов В.В., Тихонова М.В. Применение индексного метода глобальной оптимизации при решении обратных задач химической кинетики // Вычислительные методы и программирование. 2011. T. 12. № 1. С. 127–135.

2.    Исмагилова А.С., Пыжьянова Л.Р., Спивак С.И. Автоматизация метода декомпозиции для анализа информативности кинетических измерений при решении обратных задач // Вестн. Башкирского ун-та. 2016. Т. 21. № 1. С. 9–13.

3.    Седова Н.А., Седов В.А. Логико-лингвистическая модель оценки уровня аварийных ситуаций // Современная наука: актуальные проблемы теории и практики. 2016. № 2. С. 65–69.

4.    Степашина Е.В. Оптимизация финансовых показателей предприятия на основе нейросетевой модели // Информационные системы и технологии. 2014. № 5. С. 34–42.

5.    Canayaz M., Karci A. Cricket behavior based evolutionary computation technique in solving engineering optimization problems. Applied Intelligence, 2016, vol. 44, pp. 362–376.

6.    Zaheer H., Pant M., Kumar S., Monakhov O., Monakhova E., Deep K. A new guiding force strategy for differential evolution. Intern. J. of System Assurance Engineering and Management, 2015, vol. 6, pp. 1–14. DOI: 10.1007/s13198-014-0322-6.

7.    Антипина Е.В., Антипин А.Ф. Алгоритм расчета оптимальных начальных концентраций веществ химических реакций // Вестн. Технологического ун-та. 2017. Т. 20. № 13. С. 84–87.

8.    Karci A. Differential evolution algorithm and its variants. Anatolian J. of Computer Sciences, 2017, vol. 2, no. 1, pp. 10–14.

9.    Седова Н.А. Нечеткая продукционная модель первичной оценки опасности столкновения су- дов // Мир транспорта. 2015. Т. 13. № 2. С. 200–206.

10. Вайтиев В.А., Мустафина С.А. Построение двусторонних оценок решения прямой задачи химической кинетики // Журнал Средневолжского математического об-ва. 2012. Т. 14. № 4. С. 18–25.

References

1. Gubaydullin I.M., Ryabov V.V., Tikhonova M.V. Application of the global optimization index method to solving inverse problems of chemical kinetics. Numerical Methods and Programming. 2011, vol. 12, no. 1, pp. 127–135 (in Russ.).
2. Ismagilova A.S., Pyzhyanova L.R., Spivak S.I. Automation of decomposition method for the analysis of informativity of kinetic measurements in the inverse problem. Bull. of Bashkir University. 2016, vol. 21,
   no. 1, pp. 9–13 (in Russ.).
3. Sedova N.A., Sedov V.A. The logical-linguistic model for assessing of the emergency level. Modern Science: Actual Problems of Theory and Practice. 2016, no. 2, pp. 65–69 (in Russ.).
4. Stepashina E.V. Optimization the financial performance of enterprise on neural network model. Information Systems and Technologies. 2014, no. 5, pp. 34–42 (in Russ.).
5. Canayaz M., Karci A. Cricket behavior based evolutionary computation technique in solving engineering optimization problems. Applied Intelligence. 2016, vol. 44, pp. 362–376.
6. Zaheer H., Pant M., Kumar S., Monakhov O., Monakhova E., Deep K. A new guiding force strategy for differential evolution. Int. J. of Syst. Assurance Eng. and Management. 2015, vol. 6, pp. 1–14. DOI: 10.1007/s13198-014-0322-6.
7. Antipina E.V., Antipin A.F. Algorithm for calculating the optimal initial concentrations of substances of chemical reactions. Bulletin of Technological University. 2017, vol. 20, no. 13, pp. 84–87 (in Russ.).
8. Karci A. Differential evolution algorithm and its variants. Anatolian J. of Computer Sciences. 2017,
   vol. 2, no. 1, pp. 10–14.
9. Sedova N.A. Fuzzy production model for initial evaluating of the risk of collisions. World of Transport and Transportation J. 2015, vol. 13, no. 2, pp. 200–206 (in Russ.).
10. Vaytiev V.A., Mustafina S.A. Creation of bilateral estimates of the solution of a direct problem of chemical kinetics. Middle Volga Mathematical Society J. 2012, vol. 14, no. 4, pp. 18–25 (in Russ.).