Journal influence
Bookmark
Next issue
Using discrete optimization tools to classify cognitive deficits: special aspects of using the minimax and additive criterion
Abstract:The paper devoted to the development of discrete optimization methods for solving the applied problem of clustering the cognitive resources of patients with coronary artery disease (CAD). The methods reflect the prospects of their surgical treatment. Many indicators of different cognitive functions and brain activity are used to determine the cognitive deficits associated with aging and concomitant cerebrovascular atherosclerosis. Coronary artery bypass grafting, which is widely used to treat CAD patients, increases the risk of postoperative cognitive deficits. In this regard, it is im-portant to identify the most informative markers of the cognitive status in patients in the preopera-tive state. To classify this state, the authors use the hemispheric activity characteristics, i.e. lateral-ized power of the theta, alpha, and beta rhythms together with the indicator of minimal cerebral dys-function (MMSE) and the integral cognitive indicator based on a set of parameters obtained during a recording sensory-motor responses and testing attention and memory in 114 male patients admitted to the clinic for coronary artery bypass grafting. The average patient’s age is 55.9 ± 5.3 years; 90 of them had secondary education and 32 had higher education. The results of computational experiments with clustering indicators of psychometric and neuro-physiological testing of CAD patients have shown the effectiveness of the developed toolkit for clustering by the discrete optimization means and the best discriminatory capabilities due to the ad-ditive criterion.
Аннотация:Статья посвящена разработке методов дискретной оптимизации для решения прикладной задачи кластеризации когнитивных ресурсов пациентов с ишемической болезнью сердца. Данные методы отражают перспективность оперативного лечения таких пациентов. Для определения когнитивного дефицита, связанного со старением и сопутствующим атеросклерозом сосудов мозга, применяют множество показателей разных когнитивных функций и активности мозга. Широко используемое для лечения пациентов с ишемической болезнью сердца коронарное шунтирование усиливает риск возникновения послеоперационного когнитивного дефицита. В связи с этим актуально выявление наиболее информативных маркеров предоперационного со-стояния когнитивного статуса пациентов. Для его классификации использованы характеристики полушарной активности мозга на частотах тета-, альфа- и бета-диапазонов совместно с показателем минимальных мозговых дисфункций и интегральным показателем, который сформирован на основе комплекса параметров, полученных при регистрации сенсорно-моторной реакции и характеристик внимания и памяти группы пациентов. Результаты вычислительных экспериментов с кластеризацией показателей психометрического и нейрофизиологического тестирования пациентов с ишемической болезнью сердца по-казали эффективность разработанного инструментария кластеризации с применением дискретной оптимизации и лучшие дискриминационные возможности при использовании аддитивного критерия.
| Authors: Razumnikova O.M. (razoum@mail.ru) - Novosibirsk State Technical University (Professor), Novosibirsk, Russia, Ph.D, Mezentsev Yu.A. (mesyan@yandex.ru) - Novosibirsk State Technical University (Professor), Novosibirsk, Russia, Ph.D, Pavlov P.S. (fuzzokolobok@gmail.com) - Novosibirsk State Technical University (Senior Lecturer), Novosibirsk, Russia, Tarasova I.V. (iriz78@mail.ru) - State Research Institute for Complex Issues of Cardiovascular Diseases (Leading Researcher), Kemerovo, Russia, Ph.D, Trubnikova O.A. (olgalet17@mail.ru) - State Research Institute for Complex Issues of Cardiovascular Diseases (Head of Laboratory), Kemerovo, Russia, Ph.D | |
| Keywords: clusterization, minimax quality criterion, additive function, linear relaxation, binary cuts and branches algorithm, cognitive deficit detection |
|
| Page views: 4901 |
PDF version article |
Вычислительные эксперименты с кластеризацией данных нейрофизиологического тестирования с использованием оригинальной формальной постановки задачи смешанного целочисленного программирования, или milp (mixed linear programming), с минимаксным критерием и адаптированного под нее алгоритма бинарных отсечений и ветвлений авторы проводили и ранее. Перспективы применения разработанного метода для классификации пациентов с ишемией мозга вследствие сердечно-сосудистых заболеваний показаны в [1]. Было установлено, что разработанный способ кластеризации переменных обладает хорошими дискриминационными возможностями и может быть полезен для различения разных по своим свой- ствам исследуемых групп. Известно, что ишемическая болезнь сердца сопровождается гипоксическими явлениями в мозге, ослаблением кровотока и связанным с этими эффектами когнитивным дефицитом. Среди значимых факторов снижения когнитивного статуса пациентов и риска его ухудшения после оперативного вмешательства отмечают возраст и уровень образования [2–5]. С другой стороны, в качестве предиктора послеоперационной корковой дисфункции (ПОКД) рассматриваются частотно-пространственные изменения полушарной активности мозга [6, 7]. Выводы о влиянии перечисленных факторов сделаны преимущественно с применением регрессионного анализа или сравнения разных групп пациентов, у которых ПОКД чаще диагностируется на основе показате- ля минимальных мозговых дисфункций (MMSE) как стандартного критерия деменции. В силу своей простоты MMSE широко применяется в клинических исследованиях, однако многие авторы признают, что такой подход недостаточно информативен и не позволяет дифференцировать пациентов по степени нарушения у них когнитивных функций и типу развития деменции [8, 9]. В связи с этим для оценки когнитивного статуса пациентов с сердечно-сосудистыми патологиями применяют батареи разнообразных методик для определения внимания и памяти, что затрудняет сопоставление полученных результатов и приводит к противоречивым выво- дам [10, 11]. Следовательно, требуются новые методы многопараметрического анализа данных. Для выяснения особенностей когнитивного профиля пациентов с сердечно-сосудистыми заболеваниями и классификации их на этой основе для персонализированного выбора способа лечения и реабилитации применяются разные методы кластерного анали- за [11–13]. Заключение о различном профиле когнитивных функций у пациентов с сердечной недостаточностью сделано с применением агломеративно-иерархического кластерного анализа [13]. Три выделенных кластера различались не только по когнитивному статусу, но и по возрасту, расе, образованию, социоэкономическому статусу и диабету, но не по настроению, тревоге, сердечно-сосудистым или легочным заболеваниям. C применением комбинации иерархического кластерного анализа для выбора начального набора кластеров с последующим применением метода К-средних также выделены три группы лиц: когнитивно интактных, с нарушениями памяти и с глобальными нарушениями [11]. Для анализа был использован массив социально-демографических показателей, MMSE и результатов выполнения тестов для оценки внимания, памяти и вербальных функций. Авторы подчеркивают важность индивидуально дифференцированной оценки когнитивного профиля пациентов, так как его гетерогенность важна для выбора оптимального способа лечения. Такой же подход с объединением этих двух стандартных методов кластерного анализа использован для определения групп с кардиореспираторной нестабильностью [12]. Выделенные кластеры наряду с частотой дыхания и сердечных сокращений различались по возрасту, количеству сопут- ствующих заболеваний и продолжительности пребывания в больнице. Подчеркивается необходимость дальнейших исследований для определения общих или специфических физиологических основ кластеров для принятия оптимальных клинических решений при первых проявлениях кардиореспираторной нестабильности. Показано, однако, что кластеризация на основе К-средних существенно зависит от выбора начальных кластерных центров, поэтому разрабатываются другие алгоритмы оптимизации кластеризации, например, дополнения метода K-ближайших соседей логистической регрессией в качестве метаклассификато- ра [14], оптимальной дискретизации дан- ных [15] или машинного обучения на основе опорных векторов и других гибридных методов [16, 17]. Высокая частота встречаемости ПОКД после коронарного шунтирования, широко использующегося в современной кардиологии, обусловливает актуальность выявления наиболее информативных психометрических и/или нейрофизиологических маркеров предоперационного состояния пациентов, характеризующих их когнитивный статус. В связи с этим целью настоящей работы стал поиск наилучшей дифференциации когнитивного состояния пациентов с ишемической болезнью сердца. Для выявления таких групп был использован метод кластеризации по множеству социально-демографических, психометрических и нейрофизиологических показателей посредством аппарата дискретной оптимизации с применением минимаксного или аддитивного критерия и последующим сравнением результатов этих вычислений. Содержательная и формальная постановки задачи оптимальной кластеризации многомерных объектов по множеству показателей В качестве исходных данных для кластеризации использованы когнитивные показатели, измеренные с помощью тестов, и нейрофизиологические, снятые посредством электроэнцефалограммы (ЭЭГ). Собранные данные характеризуют 114 объектов. Основной особенностью постановки задачи кластеризации является ориентация на минимизацию суммарных расстояний между всеми объектами, включаемыми в кластер. В отличие от стандартного подхода, используемого в методе к-центров [18], результаты применения описываемого инструментария не зависят от выбора начальных приближений к решению. С одной стороны, его применение приводит к усложнению постановки с образованием NP-трудной задачи и соответствующих алгоритмов, а с другой, позволяет получать наиболее качественные разбиения на кластеры. При этом, как показывают вычислительные эксперименты, подход совместим с методом к-центров для поиска начального приближения, а последовательное применение обоих подходов с обучающей выборкой для первого снимает проблему размерности при сохранении качества разбиений. Приведем формальную постановку задачи оптимальной кластеризации. Будем именовать ее оптимальной m-кластеризацией (с разбиением множества объектов в метрическом пространстве на m кластеров) для общего случая. Введем обозначения: Обозначим ci,j расстояния между объектами i и j, Определим переменные Тогда задача кластеризации будет состоять в определении булевых переменных Условия выбора:
линеаризующие посредством замены
Добавив в задачу условия, реализующие минимаксный критерий
имеющий смысл минимизации максимальной по всем кластерам суммы расстояний между всеми объектами каждого кластера, получим (1)–(5) – вариант формализации задачи оптимальной кластеризации многомерных объектов по множеству показателей. Минимаксный критерий (5) эффективен при разбиении исходного множества на максимально однородные подмножества с одновременной минимизацией сумм расстояний между объектами. Кроме критерия (5), в зависимости от содержательного смысла задачи кластеризации в ряде случаев более приемлемым является аддитивный критерий, который удобно представлять в виде
Здесь lk – сумма расстояний между всеми парами объектов в кластере k, Решение варианта задачи m-кластеризации (1)–(4), (6), (7) позволяет находить разбиения множества объектов с заданными расстояниями между всеми парами объектов на заданное число (m) подмножеств (кластеров), которое гарантирует минимизацию суммы минимальных суммарных расстояний между всеми парами объектов по всем кластерам. В совокупности условия (6) и (7) реализуют аддитивный критерий кластеризации, наиболее часто используемый для разбиения множеств объектов на максимально непохожие (отдаленные друг от друга по суммам расстояний между объектами) подмножества. Следует отметить, что для сокращения трудоемкости обеих постановок milp можно заменить зависимые булевы переменные
Доказательство эквивалентности задач оптимальной m-кластеризации (1)–(5), (1)–(4), (6), (7) и (1)–(3), (5), (8), (1)–(3), (6)–(8) соответственно приведено в работе [1]. Трудоемкость задачи оптимальной кластеризации многомерных объектов и средства решения В работе [1] также показана принадлежность обеих постановок milp (1)–(3), (5), (8) и (1)–(3), (6)–(8) классу NP. Это означает, что для представленных выше вариантов задач кластеризации не существует теоретически эффективных алгоритмов. Однако для практического применения в достаточной степени разработаны алгоритмы, которые можно именовать как условно экспоненциальные. Несмотря на недоказанность эффективности, данные алгоритмы позволяют за разумное время находить оптимальные (либо приближенные к оптимальным) решения представленных задач дискретной оптимизации. Примером такого алгоритма может служить алгоритм бинарных отсечений и ветвлений [19]. В качестве стандартных средств решения также могут применяться модуль Gurobi optimization либо IBM CPLEX optimization studio. Средства последнего применены для поиска решения сформулированных выше задач кластеризации (1)–(3), (5), (8) и (1)–(3), (6)–(8). В частности, для решения обеих задач ис- пользованы язык OPL (optimization program language) и вычислительные модули CPLEX, реализующие барьерный метод в качестве оценочного и алгоритмы смешанного программирования (ветвей и отсечений, ветвей и границ). Далее приводится содержательная интерпретация результатов обработки данных медико-психологических исследований на основе формальных постановок (1)–(3), (5), (8) и (1)–(3), (6)–(8) средствами IBM CPLEX optimization studio. Результаты применения разработанного инструментария кластеризации когнитивных и нейрофизиологических показателей для сравнения эффективности минимаксного и аддитивного критериев Для выяснения дискриминационных возможностей разработанного метода кластеризации использованы показатели когнитивных функций и ЭЭГ пациентов НИИ комплексных проблем сердечно-сосудистых заболеваний (114 пациентов-мужчин, поступивших в клинику для проведения операции коронарного шунтирования; средний возраст – 55,9±5,3 лет; 90 имели среднее и 32 высшее образование). Для оценки когнитивного статуса пациентов наряду с MMSE применяли интегральный когнитивный показатель (ИКП), сформированный на основе комплекса параметров, полученных при регистрации сенсорно-моторной реакции и характеристик внимания и памяти, с использованием психофизиологического программно-аппаратного комплекса Status PF [2]. ЭЭГ была зарегистрирована в состоянии покоя с закрытыми глазами монополярно в 62 отведениях. Показатели мощности ЭЭГ после удаления артефактов рассчитаны на основе быстрого преобразования Фурье. Более подробно методики регистрации и анализа ЭЭГ описаны в ряде ранее опубликованных ра- бот [6, 7]. Для статистического анализа данных были использованы показатели мощности тета- (4–6 Гц), альфа- (8–10 Гц) и бета- (20–30 Гц) ритмов, усредненные для левого и правого полушарий. Для анализа мощности тета-, альфа- и бета-ритмов в левом и правом полушариях совместно с показателями MMSE и ИКП применен представленный выше инструмента- рий кластеризации на базе задач milp (1)–(3), (5), (8) и (1)–(3), (6)–(8). Все исходные показатели В результате выполненных расчетов с применением минимаксного критерия (5) были выделены три кластера, в каждый из которых вошли по 36–45 пациентов. Анализ составов пациентов в этих кластерах показал относительную устойчивость при сравнении лево- и правополушарных показателей мощности исследованных ритмов при их изменении для разных частотных диапазонов, так как большая часть пациентов из кластеров 1 и 2, сформированных на основе низкочастотных тета- и альфа-ритма, перешла, соответственно, в кластеры 2 и 1 на частоте бета-осцилляций. Для выяснения особенностей мощности ритмов в кластерах использован однофакторный дисперсионный анализ ANOVA для переменной КЛАСТЕР (3). Результаты анализа для показателей мощности биопотенциалов в левом и правом полушариях в трех частотных диапазонах, различающихся показателями как ЭЭГ, так и когнитивного статуса, представлены в таблице 1. Аналогично были выполнены вычисления с применением аддитивного критерия (7) (табл. 2). Как видно из сравнения данных, представленных в таблицах 1 и 2, применение кластеризации с аддитивным критерием позволяет лучше дифференцировать группы пациентов по показателям MMSE, ИКП и ЭЭГ во всех частотных диапазонах (F и η в таблице 2 для всех частотных диапазонов выше, чем представленные в таблице 1), особенно для правополушарной мощности бета2-ритма.
Согласно полученным результатам, различия MMSE и ИКП между кластерами значимы при анализе для каждого из параметров ЭЭГ, что подтверждает дискриминационные возможности разработанного метода кластеризации. Вместе с этим применение аддитив- ного критерия позволяет выделить группы, различающиеся по возрасту, который признается важным фактором развития когнитивного дефицита [3–6]. Заключение Поиск информативных методов определения когнитивного дефицита при старении и сопутствующем ему развитии патологических состояний организма остается актуальным направлением междисциплинарных исследований. Используемые в настоящее время разнообразные показатели активности мозга и функций внимания и памяти свидетельствуют о широком диапазоне их возрастных изменений и разной степени вовлечения компенсаторных ресурсов мозга как в дооперационном состоянии, так и для предотвращения риска возникновения послеоперационного когнитивного дефицита, который может сопутствовать любым оперативным вмешательствам с применением анестезии. Результаты вычислительных экспериментов с кластеризацией показателей психометрического и нейрофизиологического тестиро- ваний пациентов с ишемической болезнью сердца с использованием разбиений по множеству этих переменных посредством аппарата дискретной оптимизации показали эффективность разработанного инструментария оптимальной кластеризации и лучшие дискриминационные возможности при применении аддитивного критерия. Этот новый подход может быть использован не только для оценки предоперационного состояния когнитивного статуса пациентов, но и для прогноза риска развития послеоперационного когнитивного дефицита и разработки индивидуальных методов нейрореабилитации. Метод кластеризации с дискретной оптимизацией имеет широкие перспективы применения в медицине, психологии и педагогике, так как позволяет с использованием минимаксного или аддитивного критерия сформировать кластеры, оптимально дифференцированные согласно множеству показателей, информативных с позиций разных форм описания состояния здоровья или поведения человека. Работа поддержана РФФИ, проект № 19-29-01017. Литература 1. Мезенцев Ю.А., Разумникова О.М., Тарасова И.В., Трубникова О.А. О некоторых задачах кластеризации больших данных по минимаксным и аддитивным критериям, применение в медицине и нейрофизиологии // Информационные технологии. 2019. Т. 25. № 10. С. 602–608. DOI: 10.17587/it.25.602-608. 2. Трубникова О.А., Тарасова И.В., Артамонова А.И., Сырова И.Д., Барбараш О.Л. Возраст как фактор риска когнитивных нарушений у пациентов, перенесших коронарное шунтирование // Журнал неврологии и психиатрии им. С.С. Корсакова. 2011. Т. 111. № 8. С. 46–49. 3. Benson R.A., Ozdemir B.A., Matthews D., Loftus I.M. A systematic review of postoperative cognitive decline following open and endovascular aortic aneurysm surgery. The Annals of The Royal College of Surgeons of England, 2017, vol. 99, no. 2, pp. 97–100. DOI: 10.1308/rcsann.2016.0338. 4. Glumac S., Kardum G., Karanovic N. Postoperative cognitive decline after cardiac surgery: A narrative review of current knowledge in 2019. Medical Science Monitor, 2019, vol. 25, pp. 3262–3270. DOI: 10.12659/MSM.914435. 5. Snyder B., Simone S.M., Giovannetti T., Floyd T.F. Cerebral hypoxia: Its role in age-related chronic and acute cognitive dysfunction. Anesthesia and Analgesia, 2021, vol. 132, no. 6, pp. 1502–1513. DOI: 10.1213/ANE.0000000000005525. 6. Трубникова О.А., Тарасова И.В., Мамонтова А.С., Сырова И.Д., Малева О.В., Барбараш О.Л. Структура когнитивных нарушений и динамика биоэлектрической активности мозга у пациентов после прямой реваскуляризации миокарда // Российский кардиологический журнал. 2014. № 8. С. 57–62. DOI: 10.15829/1560-4071-2014-8-57-62. 7. Тарасова И.В., Трубникова О.А., Барбараш О.Л., Барбараш Л.С. Изменения электроэнцефалограммы у пациентов с ранней и стойкой послеоперационной когнитивной дисфункцией при коронарном шунтировании с искусственным кровообращением // Неврологический журнал. 2017. Т. 22. № 3. С. 136–141. 8. Тарасова И.В., Трубникова О.А., Кухарева И.Н., Барбараш О.Л. Методические подходы к диагностике послеоперационной когнитивной дисфункции в кардиохирургической клинике // Комплексные проблемы сердечно-сосудистых заболеваний. 2015. № 4. С. 73–78. 9. Davis K.K., Allen J.K. Identifying cognitive impairment in heart failure: a review of screening measures. Heart and Lung, 2013, vol. 42, no. 2, pp. 92–97. DOI: 10.1016/j.hrtlng.2012.11.003. 10. Трубникова О.А., Тарасова И.В., Артамонова А.И. и др. Нейродинамические показатели у пациентов с ишемической болезнью сердца до и после операции коронарного шунтирования // Кардиология и сердечно-сосудистая хирургия. 2011. № 4. С. 10–13. 11. Miller L.A., Spitznagel M.B., Alosco M.L., Cohen R.A., Raz N., Sweet L.H. et al. Cognitive profiles in heart failure: A cluster analytic approach. J. of Clinical and Experimental Neuropsychology, 2012, vol. 34, no. 5, pp. 509–520. DOI: 10.1080/13803395.2012.663344. 12. Bose E.L., Clermont G., Chen L., Dubrawski A.W., Ren D., Hoffman L.A., Pinsky M.R., Hravnak M. Cardiorespiratory instability in monitored step-down unit patients: using cluster analysis to identify patterns of change. J. of Clinical Monitoring and Computing, 2018, vol. 32, no. 1, pp. 117–126. DOI: 10.1007/s10877-017-0001-7. 13. Hawkins M.A., Schaefer J.T., Gunstad J., Dolansky M.A. et al. What is your patient's cognitive profile? Three distinct subgroups of cognitive function in persons with heart failure. ANR, 2015, vol. 28, no. 2, pp. 186–191. DOI: 10.1016/j.apnr.2014.10.005. 14. Shorewala V. Early detection of coronary heart disease using ensemble techniques. IMU, 2021, art. 100655. DOI: 10.1016/j.imu.2021.100655. 15. Han Y., Zhu L., Cheng Z., Li J., Liu X. Discrete optimal graph clustering. IEEE Transactions on Cybernetics, 2020, vol. 50, no. 4, pp. 1697–1710. DOI: 10.1109/TCYB.2018.2881539. 16. Kausar N., Abdullah A., Samir B.B., Palaniappan S., AlGhamdi B.S., Dey N. Ensemble clustering algorithm with supervised classification of clinical data for early diagnosis of coronary artery disease. J. of Medical Imaging and Health Informatics, 2016, vol. 6, no. 1, pp. 78–87. DOI: 10.1166/jmihi.2016.1593. 17. Verma L., Srivastava S., Negi P.C. A hybrid data mining model to predict coronary artery disease cases using non-invasive clinical data. J. of Medical Systems, 2016, vol. 40, no. 7, art. 178. DOI: 10.1007/s10916-016-0536-z. 18. Айвазян С.А., Бухштабер В.М., Еников И.С., Мешалкин Л.Д. Прикладная статистика: классификация и снижение размерности. М.: Финансы и статистика, 1989. 608 с. 19. Mezentsev Y. Binary cut-and-branch method for solving mixed integer programming problems. Constructive Nonsmooth Analysis and Related Topics (dedicated to the memory of V.F. Demyanov) (CNSA), 2017, pp. 1–3. DOI: 10.1109/cnsa.2017.7973989. References
|
| Permanent link: http://swsys.ru/index.php?id=4852&lang=en&page=article |
Print version |
| The article was published in issue no. № 4, 2021 [ pp. 579-588 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Кластеризация документов интеллектуального проектного репозитария на основе FCM-метода
- Метод ситуационного прогнозирования появления новых технологий Индустрии 4.0
- Информационно-коммуникационная технология комплексного управления деятельностью студентов
- Применение технологии CUDA для обучения нейронной сети Кохонена
- Трехтактная кластеризация динамичных интернет-ресурсов с применением DOM-моделей
Back to the list of articles
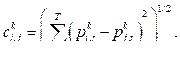
 (4)
(4)


