В настоящее время активно разрабатываются и применяются математические и компьютерные модели химических реакций (ХР), на основе которых можно прогнозировать возможность протекания тех или иных ХР, а также подбирать оптимальные условия для них. При использовании этих моделей возникает задача оценки эффективности условий проведения ХР с учетом таких факторов, как наличие примесей, стоимость катализаторов, а также других, влияющих на стоимость технологического процесса. Так как факторы, влияющие на протекание реакций, имеют различную природу, их крайне сложно сравнивать при оценке эффективности условий ХР.
Один из подходов, применяемых для оценки значимости того или иного фактора, основан на возможности применения методов интеллектуального анализа данных. Эти методы предполагают возможность накопления доста- точно репрезентативной БД.
Пусть имеется ХР, в результате которой при взаимодействии исходных веществ S1, S2, …, Sn и выполнении ряда условий φ1, φ2, …, φk образуются продукты P1, P2, …, Pm. Как правило, при протекании ХР образуются один основной продукт и один или несколько побочных. Под условиями понимаются параметры, при которых протекает ХР – температура, давление, состав катализаторов.
Важнейшей характеристикой полноты протекания ХР является выход продукта – отношение количества продукта к его теоретически возможному значению:
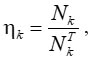 (1) (1)
где Nk – фактическое количество вещества продукта, полученного в результате реакции; NTk – максимально возможное количество вещества продукта, которое теоретически можно получить в результате реакции. Примем, что для конкретной реакции при заданном наборе исходных веществ имеется отображение набора условий реакции на вектор выходов продуктов:
{φ1, φ2, …, φk} ® {w1, w2, …, wn}. (2)
Данное отображение может быть получено разными способами:
- как результат измерений при проведении экспериментов;
- задано аналитической функцией, построенной на основе теоретических выкладок;
- как результат математического моделирования процесса протекания ХР.
Пусть отображение (2) получено некоторым способом. Встает вопрос о том, как оценить его эффективность и как приписать ему некую оценку оптимальности, позволяющую выделить среди множества отображений те, которые имеют максимальные оценки эффективности реакции. Возможность построения таких оценок позволит подбирать оптимальные условия протекания ХР.
В данной работе для оценки эффективности ХР предлагается вначале независимо оценить эффективность каждого фактора, а затем построить суммарную оценку, учитывающую эффективность каждого из них.
В этом случае удается оценить значимость факторов, используя такие методы, как построение ассоциативных правил и правил, извлекаемых из построения деревьев классификации, другие алгоритмы. В работах [1, 2] авторы также использовали такой подход, получая оценки значимости факторов на основе как содержащей экспериментальные данные, так и построенной модельной БД. Применяемый комплекс алгоритмов позволял получать оценки и на качественном, и на количественном уровне.
В данной работе предлагается другая методика оценки эффективности ХР, учитывающая различные условия ее протекания (например, давление и температура). Этот подход ближе к методам нечеткой логики.
Предложения по построению оценок проиллюстрированы следующим примером отображения (2), полученного на основе экспериментальных данных, заимствованным из рабо- ты [3] (табл. 1).
В таблице 1 представлены результаты шести экспериментов, полученные за одинаковое время. Во втором и третьем столбцах отражается выход целевого и побочного продуктов, в четвертом и пятом – условия протекания реак- ции: температура и давление соответственно.
Таблица 1
Экспериментальные данные: продукты и условия протекания реакции
Table 1
Experimental data: reaction products and conditions
|
Эксперимент
|
ηtar
|
ηside
|
T
|
P
|
|
1
|
0.69
|
0.03
|
438.15
|
30
|
|
2
|
0.79
|
0.01
|
458.15
|
30
|
|
3
|
0.78
|
0.10
|
478.15
|
30
|
|
4
|
0.93
|
0.04
|
498.15
|
30
|
|
5
|
0.56
|
0.36
|
498.15
|
20
|
|
6
|
0.69
|
0.05
|
498.15
|
40
|
Оценка эффективности условий протекания реакции
Данная оценка является важной задачей и представляет значительный интерес при управлении химическими производствами и выборе режимов технологических процессов. Очевидно, что выбор наиболее эффективных условий является задачей принятия решений при нечеткой исходной информации. Так, сложно сформулировать, эффективно ли проводить реакцию с меньшим выходом целевого продукта при меньшей температуре либо с большим выходом продукта при более высокой температуре, затрачивая ресурсы на нагрев. Кроме того, условия протекания имеют различную физическую природу, измеряются в различных единицах, и их сравнение крайне затруднительно. В ряде работ оценивалась эффективность влияния отдельных факторов на конечный результат. В работах [4, 5] оценивалось влияние такого фактора, как температура.
В работах [6, 7] для управления химическими процессами и оценки их эффективности применялся аппарат нечеткой логики.
В данной работе предложен иной подход к оценке эффективности.
Для каждого продукта и каждого условия ХР введем нечеткую меру эффективности – монотонную функцию со значениями из интервала [0, 1]. Над нечеткими мерами можно определить операции сложения и умножения, понимая сложение как взятие максимума из двух мер, а умножение как взятие минимума [7–9]. Сохраняя понимание эффективности условия как нечеткой меры, предложим способ построения общей оценки эффективности ХР на основе частных оценок:
es = F(etar, …, eT, ep), es Î [0, 1]. (3)
Будем рассматривать суммарную эффективность ХР как возможность получения бонусов – за получение продукта ХР, за минимизацию затрат для достижения условий протекания реакции.
Оценка эффективности полноты протекания ХР
Важнейшей характеристикой полноты протекания ХР является выход продуктов.
При протекании ХР в зависимости от условий образуется некоторое количество целевого и побочных продуктов, при этом на практике получается значительно меньше вещества, чем это теоретически возможно. Так что, ηk принадлежит интервалу [0, 1], поэтому выход целевого продукта можно использовать в качестве меры эффективности по целевому продукту:
etar = htar. (4)
На образование побочных продуктов расходуется субстрат, и к тому же возникает необходимость удаления побочного продукта, что снижает эффективность протекания реакции. С учетом сказанного построим функцию εside, задающую оценку эффективности по побочному продукту:
eside = 1 – h side. (5)
Эффективность etar и eside можно интерпретировать как бонусы за получение основного продукта и за минимизацию побочного.
Оценки эффективности условий протекания реакции
Построение оценки эффективности для продуктов (основных и побочных) вполне естественно: чем больше на выходе основного продукта и чем меньше побочного, тем выше должна быть суммарная эффективность ХР.
Рассматривая условия протекания ХР, следует скорее говорить о затратах на поддержание нужных условий: чем выше температура, давление, требуемое для проведения реакции, тем выше затраты и, соответственно, ниже общая эффективность. Чтобы разумным образом задать оценку эффективности того или иного условия, введем понятие мягкого условия [10].
Мягкое значение условия – это такое значение, при котором затраты на выполнение условия минимальны, что означает максимальную эффективность.
Например, если ХР может протекать при нормальной комнатной температуре, то значе- ние комнатной температуры и представляет мягкое условие. Для условия V наряду с параметром Vs, задающим мягкое значение, введем еще два параметра – Vmin и Vmax – минимально и максимально допустимые значения условия. Для этих значений естественно предположить, что затраты будут максимальными, а эффективность минимальной. Понятно, что выполняется естественное соотношение
Vmin £ Vs £ Vmax. (6)
Тем самым сформулированы требования к функции ε. На интервале [Vmin, Vs] функция монотонно возрастает от 0 до 1, а на интервале [Vs, Vmax] монотонно убывает от 1 до 0.
Простейшим вариантом такой функции является треугольная функция:
 (7) (7)
Следует отметить, что оценка эффективности для основного и побочного продуктов – это частный случай треугольной функции. На рисунке 1 представлен график функции для условий Pmin = –2 атм, Pmax = 10 атм, Ps = 1 атм.
Учитывая специфику условия, мера может быть задана более сложной функцией. Не приводя доводов, учитывающих специфику организации температурного режима, зададим функцию для температуры:
 (8) (8)
 Несмотря на сложную форму записи (8), функция задает гладкую колоколообразную функцию, подобную гауссиане, для случая, когда мягкие условия симметричны относительно краевых значений. На рисунке 2 показан график такой функции для случая Tmin = 100 K, Tmax = 500 K, TS = 300 K. Несмотря на сложную форму записи (8), функция задает гладкую колоколообразную функцию, подобную гауссиане, для случая, когда мягкие условия симметричны относительно краевых значений. На рисунке 2 показан график такой функции для случая Tmin = 100 K, Tmax = 500 K, TS = 300 K.
Построение суммарной оценки эффективности ХР
Учитывая, что в предлагаемом подходе эффективность получения продуктов и условий можно рассматривать как нечеткую меру, суммарную эффективность можно определить как минисвязную функцию:
 (9) (9)
В данном случае такой подход не позволяет учесть вклад каждого фактора, поэтому разумнее суммарную эффективность определить как среднее значение всех факторов:
 (10) (10)
В этом случае общая эффективность находится в пределах [0, 1].
Исходя из предложенного подхода интерпретации эффективности как получение бонусов, можно предложить вычислять эффективность как средневзвешенное значение полученных бонусов.
Тогда
 (11) (11)
Коэффициент а – это число бонусов, назначаемых за единицу эффективности.
Такой подход позволяет ранжировать вклад различных факторов в общую эффективность. Например, можно использовать параметры atar = 100, а aside = aT = aP = 50, существенно увеличив вклад целевого продукта в общую эффективность.
 В таблице 2 отражены результаты оценки эффективности для условий из таблицы 1. В первом столбце таблицы задан номер эксперимента. В следующих четырех столбцах представлены данные об эффективности отдельных факторов – выхода целевого и побочного продуктов, температуры и давления. В трех последних – данные о суммарной эффективности эксперимента, рассчитанные соответственно по формулам (9)–(11). В таблице 2 отражены результаты оценки эффективности для условий из таблицы 1. В первом столбце таблицы задан номер эксперимента. В следующих четырех столбцах представлены данные об эффективности отдельных факторов – выхода целевого и побочного продуктов, температуры и давления. В трех последних – данные о суммарной эффективности эксперимента, рассчитанные соответственно по формулам (9)–(11).
Использование оценки эффективности в соответствии с формулой (10) для большого количества параметров не работает. Оценка (9) с точки зрения информативности уступает оценке по формуле (11). Результат оценки по формуле (11) четко отображает влияние на эффективность выхода целевого и побочного продуктов, но с выбранными параметрами (atar = 100, aside = aT = aP = 50) практически не учитывает влияние давления. Очевидно, подбор параметров решает данную проблему.
Заключение
В статье предложена методика оценки эффективности протекания ХР с учетом ключе- вых характеристик, по которым можно судить об эффективности: выхода продуктов, температуры, давления. Предложенная методика с назначением бонусов позволяет учитывать вклад характеристик с различным физическим смыслом и различными единицами измерения. Наиболее приемлемой суммарной оценкой является средневзвешенная оценка эффективности отдельных факторов. Проблема весов может быть решена либо на основе экспертных знаний, либо с использованием результатов работы комплекса алгоритмов интеллектуального анализа данных.
Литература
1. Биллиг В.А., Звягинцев Н.В. Алгоритмы Data Mining при поиске эффективных условий проведения химических реакций // Вестн. ТвГУ. Сер.: Прикладная математика. 2021. № 4. С. 29–42. DOI: 10.26456/vtpmk625.
2. Биллиг В.А., Звягинцев Н.В. Комплекс алгоритмов Data Mining в исследовании процесса протекания химических реакций // Математические основы информатики и информационно-коммуникационных систем: Сб. тр. 2021. С. 118–124. DOI: 10.26456/mfcsics-21-19.
3. del Rıo I., Ruiz N., Claver C., van der Veen L.A., van Leeuwen P.W.N.M. Hydroxycarbonylation of styrene with palladium catalysts – the influence of the mono- and bidentate phosphorus ligand. J. of Molecular Catalysis A: Chemical, 2000, vol. 161, no. 1-2, pp. 39–48. DOI: 10.1016/S1381-1169(00)00359-9.
4. Смирнова А.И., Дягилева А.Б. Оценка влияния температуры на эффективность очистки сточных вод композиционным коагулянтом-флокулянтом на основе нефелинового сырья // Журнал прикладной химии. 2021. Т. 94. № 2. С. 256–263. DOI: 10.31857/S0044461821020146.
5. Юленец Ю.П., Марков А.В., Краснобородько Д.А. Повышение эффективности реакторов для блочной полимеризации изопрена // Журнал прикладной химии. 2020. Т. 93. № 7. С. 988–995. DOI: 10.31857/S0044461820070099.
6. Кафаров В.В., Дорохов И.Н., Марков Е.П. Системный анализ процессов химической технологии: метод нечетких множеств. М.: Юрайт, 2018. 360 с.
7. Sarmasti Emami M.R. Fuzzy logic applications in chemical processes. JMCS, 2010, vol. 1, no. 4, pp. 339–348. DOI: 10.22436/JMCS.001.04.11.
8. Орловский С.А. Проблемы принятия решений при нечеткой исходной информации. М.: Наука, 1981. 208 с.
9. Кофман А. Введение в теорию нечетких множеств; [пер. с франц.]. М.: Радио и связь, 1982. 431 с.
10. Кольцов Н.И., Федотов В.Х. Использование нечеткой логики для построения адекватных кинетических моделей химических реакций // Химия и химическая технология. 2013. Т. 56. № 9. С. 50–53.
References
- Billig V.A., Zvyagintsev N.V. Data Mining algorithms in search of effective conditions for conducting chemical reactions. Herald of Tver State University. Ser. Appl. Math., 2021, no. 4, pp. 29–42. DOI: 10.26456/vtpmk625 (in Russ.).
- Billig V.A., Zvyagintsev N.V. A set of Data Mining algorithms in the study of the process of chemical reactions. Proc. Conf. Mathematical Foundations of Computer Science and Information and Communication Systems, 2021, pp. 118–124. DOI: 10.26456/mfcsics-21-19 (in Russ.).
- del Rıo I., Ruiz N., Claver C., van der Veen L.A., van Leeuwen P.W.N.M. Hydroxycarbonylation of styrene with palladium catalysts – the influence of the mono- and bidentate phosphorus ligand. J. of Molecular Catalysis A: Chemical, 2000, vol. 161, no. 1-2, pp. 39–48. DOI: 10.1016/S1381-1169(00)00359-9.
- Smirnova A.I., Dyagileva A.B. Evaluation of the effect of temperature on the efficiency of wastewater treatment with a composite coagulant-flocculant based on nepheline raw materials. Russ. J. of Applied Chemistry, 2021, vol. 94, no. 2, pp. 252–258. DOI: 10.31857/S0044461821020146 (in Russ.).
- Yulenets Yu.P., Markov A.V., Krasnoborod’ko D.A. Rising the efficiency of the isoprene bulk polymerization apparatuses. Russ. J. of Applied Chemistry, 2020, vol. 93, no. 7, pp. 1027–1033. DOI: 10.31857/
S0044461820070099 (in Russ.).
- Kafarov V.V., Dorokhov I.N., Markov E.P. System Analysis of Chemical Technology Processes: The Method of Fuzzy Sets. Moscow, 2018, 360 p. (in Russ.).
- Sarmasti Emami M.R. Fuzzy logic applications in chemical processes. JMCS, 2010, vol. 1, no. 4,
pp. 339–348. DOI: 10.22436/JMCS.001.04.11.
- Orlovskiy S.A. Problems of Decision-Making with Fuzzy Initial Information. Moscow, 1981, 208 p.
(in Russ.).
- Jones A., Kaufmann A., Zimmermann H.-J. Fuzzy Sets Theory and Applications. NY, Masson Publ., 1986, 403 p. DOI: 10.1007/978-94-009-4682-8. (French ed.: Paris, 1977, 235 p.).
- Koltsov N.I., Fedotov V.H. Using fuzzy logic to construct adequate kinetic models of chemical reactions. Chemistry and Chemical Technology, 2013, vol. 56, no. 9, pp. 50–53 (in Russ.).
|
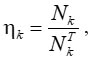 (1)
(1) (7)
(7) (8)
(8)
 (10)
(10)
