Введение. Заполнение пропущенных значений в наборах данных является важным этапом предобработки и может оказать значительное влияние на результаты анализа. Современные исследователи часто сталкиваются с проблемой пропущенных данных, которые необходимо обрабатывать, потому что отсутствие некоторых значений или их некорректное заполнение приводит к невозможности применения методов машинного обучения и принятия решения на основе имеющихся данных, делая анализ таких данных бесполезным [1]. Таким образом, нахождение эффективных методов для правильной обработки пропусков является актуальной задачей. Существуют различные методы заполнения таких значений, к наиболее простым относится заполнение средним или медианным значением по столбцу [1]. Однако такой подход к заполнению отсутствующих данных является сугубо статистическим и не учитывает возможных зависимостей в данных, принадлежащих разным столбцам [2].
Если задачу восстановления пропусков числовых данных свести к задаче прогнозирования, то одним из перспективных подходов к ее решению является применение нейронных сетей. В данной работе рассматривается обобщенная регрессионная нейронная сеть GRNN (Generalized Regression Neural Network), которая показывает лучшие результаты прогнозирования в сравнении, например, с сетями прямого распространения [3, 4].
 GRNN является разновидностью нейронных сетей с радиальным базисом, ее архитектура приведена на рисунке 1.
GRNN является разновидностью нейронных сетей с радиальным базисом, ее архитектура приведена на рисунке 1.
GRNN состоит из четырех слоев: входного, радиального, суммирования и деления, выходного.
На входной (первый) слой поступают наборы данных, функция активации нейронов входного слоя линейная:
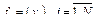 (1)
(1)
где xi - сигнал, поступающий на вход нейронов первого слоя.
Второй слой называется радиальным, каждый его нейрон воспроизводит гауссову поверхность отклика:
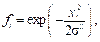 (2)
(2)
 где xi - сигнал, поступающий на вход нейронов второго слоя GRNN; σÎ[0, 1] - параметр, определяющий радиус влияния каждой базисной функции и быстроту стремления к нулю при удалении от центра (рис. 2).
где xi - сигнал, поступающий на вход нейронов второго слоя GRNN; σÎ[0, 1] - параметр, определяющий радиус влияния каждой базисной функции и быстроту стремления к нулю при удалении от центра (рис. 2).
Слой суммирования и деления передает на первый нейрон этого слоя числитель - сумму произведений значений сигналов нейронов второго слоя на значения их функций активации:
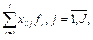 (3)
(3)
и знаменатель - сумму значений функций активации:
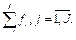 (4)
(4)
Выходной слой содержит один нейрон, он вычисляет выходные данные путем деления части числителя на часть знаменателя и предназначен для оценки взвешенного среднего [5, 6]:
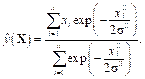 (5)
(5)
Алгоритм обучения GRRN является однопроходным. Во время обучения настраиваются веса связей между слоями GRRN и параметры, такие как σ и скорость обучения. Цель обучения GRRN - минимизировать ошибку прогнозироания, в качестве которой, как правило, вы- ступает среднеквадратичная ошибка (Mean Squared Error, MSE) [7, 8].
Достоинством сети GRNN можно считать определенность структуры: сеть вмещает в себя все обучаю- щие данные. С другой стороны, такая структура нейронной сети является ее основным недостатком, поскольку при большом объеме обучающих данных скорость работы сети падает. Однако при небольшом объеме входных данных сеть способна быстро обучаться, например, в сравнении с сетью прямого распространения. Также важно отметить, что GRNN позволяет учитывать нелинейные зависимости в данных. Это обстоятельство делает GRNN эффективным инструментом для аппроксимации сложных функций, а значит, и предсказания пропущенных значений [9, 10].
Таким образом, учитывая достоинства GRNN для решения задачи пропущенных значений в наборах данных, воспользуемся этим инструментом и сравним его со статистическим методом - заполнение средним значением по столбцу.
Описание эксперимента
В качестве входных наборов данных использованы клинико-лабораторные показатели - 142 000 наборов данных по общему анализу крови, в которых присутствуют показатели обмена железа, маркеры воспаления, ретикулоцитарные показатели и другие. Для некоторых показателей данные либо отсутствуют, либо некорректны (около 15 %).
Алгоритм заполнения пропущенных значений с применением GRNN будет следующим:
- проверить наличие пропусков в данных на этапе предварительной обработки данных;
- определить признак или признаки, в которых необходимо заполнить пропуски, – y;
- выделить из полного набора данных X часть наборов 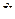 , в которых значения в строках для этого признака полностью заполнены;
, в которых значения в строках для этого признака полностью заполнены;
- обучить GRNN на наборе данных 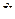 ;
;
- оценить MSE на валидационных данных из набора 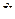 ;
;
- восстановить значения целевого столбца y в наборе данных 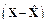 с помощью обученной модели GRNN.
с помощью обученной модели GRNN.
Для разработки модели GRNN использованы язык программирования Python, библиотеки Keras и PyGRNN. Перед обучением сети выполнена предварительная обработка данных, которая включала их нормализацию и удаление выбросов для более точного прогноза. Строки, в которых отсутствовали значения целевого столбца, в обучении не участвовали. Оставшиеся данные были поделены на тренировочную и валидационную выборки, на валидацию приходилась 1/4 часть.
На рисунке 3 представлены результаты MSE для 125 эпох обучения: на обучающей выборке ошибка обучения на последней эпохе составила 0.0144, на валидационной - 0.0377.
В ходе работы также был проанализирован набор данных, в котором количество заполненных данных для обучения составляло 150 строк. Следует отметить, что обучить модель GRNN для эффективного выявления закономерностей в данных не удалось. Можно предположить, что такой результат связан с сокращением количества наборов данных для обучения.

 Схема заполнения пропущенных значений статистическим методом приведена на рисунке 4.
Схема заполнения пропущенных значений статистическим методом приведена на рисунке 4.
Алгоритм заполнения пропущенных значений статистическим методом:
- проверить наличие пропусков в данных на этапе их предварительной обработки;
- определить номера столбцов-признаков, требующих заполнения, и для каждого такого столбца: а) найти следующую незаполненную ячейку aij, где i – номер строки, j - номер столбца-признака; б) найти математическое ожидание для заполненных данных столбца j, находящихся выше строки i: 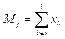 , и принять значение признака yj равным Mj; в) заполнить ячейку aij значением yj;
, и принять значение признака yj равным Mj; в) заполнить ячейку aij значением yj;
- оценить MSE на валидационных данных из набора 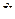 ;
;
- восстановить значения целевого столбца y в наборе данных 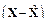 с помощью статистического метода.
с помощью статистического метода.
В таблице приведены результаты MSE, полученные на валидационных данных после применения GRNN и статистического метода соответственно.
Значения MSE на разных объемах наборов данных
MSE values on different volumes of datasets
|
Число записей
|
GRNN
|
Статистический метод
|
|
150
|
0.401
|
0.127
|
|
1 000
|
0.309
|
0.109
|
|
5 000
|
0.101
|
0.102
|
|
50 000
|
0.072
|
0.091
|
|
100 000
|
0.039
|
0.088
|
|
142 000
|
0.038
|
0.072
|
Выводы
В работе представлены методы заполнения пропущенных значений в исходных наборах данных с использованием обобщенной регрессионной нейронной сети GRNN и статистического подхода.
Как показывают результаты эксперимента, GRNN представляет собой эффективный инструмент, который можно использовать для заполнения пропущенных значений на больших наборах данных, так как он позволяет автоматически извлекать зависимости из данных и выполнять прогнозы высокой точности.
В ходе работы проанализированы небольшие наборы данных с числом заполненных данных для обучения 1 000 строк и менее, для которых не удалось обучить модель GRNN с допустимым значением MSE = 0,1. Причина высокой ошибки обучения может быть связана с небольшим количеством данных для обучения. В то же время для небольшого объема наборов данных статистический метод показывает лучшие в сравнении с GRNN результаты.
Очевидно, что представляют интерес дальнейшее исследование зависимости эффективности данного метода от количества объектов для обучения и сравнение данного подхода с другими методами.
Список литературы
1. Bozhenko V.V., Tatarnikova T.M. Application of data preprocessing in medical research. Proc. WECONF, 2023, pp. 1–4. doi: 10.1109/WECONF57201.2023.10148004.
2. Сташкова О.В., Шестопал О.В. Использование искусственных нейронных сетей для восстановления пропусков в массиве исходных данных // Изв. вузов. Северо-Кавказский регион. Технич. науки. 2017. № 1. С. 37–42.
3. Андреев П.Г., Андреева Т.В., Юрков Н.К. Использование искусственной нейронной сети типа GRNN в задачах прогнозирования // Международная конференция по мягким вычислениям и измерениям. 2017. Т. 2. С. 63–66.
4. Шпаков А.В., Лавина Т.А. Применение нейронных сетей для аппроксимации экспериментальных данных // Тенденции развития науки и образования. 2022. № 84-2. С. 60–64. doi: 10.18411/trnio-04-2022-61.
5. Sharma S., Sharma S., Athaiya A. Activation functions in neural networks. IJEAST, 2020, vol. 4, no. 12, pp. 310–316. doi: 10.33564/ijeast.2020.v04i12.054.
6. Богданов П.Ю., Пойманова Е.Д., Краева Е.В., Веревкин С.А., Татарникова Т.М. Программные среды для изучения основ нейронных сетей // Программные продукты и системы. 2021. Т. 31. № 1. С. 145–150. doi: 10.15827/ 0236-235X.133.145-150.
7. Тарик Р. Создаем нейронную сеть. М.: Диалектика, 2017. 272 c.
8. Macpherson T., Matsumoto M., Gomi H., Morimoto J., Uchibe E., Hikida T. Parallel and hierarchical neural me- chanisms for adaptive and predictive behavioral control. Neural Networks, 2021, vol. 144, pp. 507–521. doi: 10.1016/ j.neunet.2021.09.009.
9. Yu S., Jiang F., Li L., Xie Y. CNN-GRNN for image sharpness assessment. In: LNIP. Proc. CNN, 2017, vol. 10116, pp. 50–61. doi: 10.1007/978-3-319-54407-6_4.
10. Крутиков А.К. Прогнозирование спортивных результатов в индивидуальных видах спорта с помощью обобщенно-регрессионной нейронной сети // Молодой ученый. 2018. № 12. С. 22–26.
References
1. Bozhenko, V.V., Tatarnikova, T.M. (2023) ‘Application of data preprocessing in medical research’, Proc. WECONF, pp. 1–4. doi: 10.1109/WECONF57201.2023.10148004.
2. Stashkova, O.V., Shestopal, O.V. (2017) ‘Using artificial neural networks to restore gaps in the source data array’, Bull. of Higher Educational Institutions. North Caucasus Region. Tech. Sci., (1), pp. 37–42 (in Russ.).
3. Andreev, P.G., Andreeva, T.V., Yurkov, N.K. (2017) ‘Using an artificial neural network of the GRNN type in forecasting problems’, Proc. Int. Conf. SCM-2017, 2, pp. 63–66 (in Russ.).
4. Shpakov, A.V., Lavina, T.A. (2022) ‘Application of neural networks for approximation of experimental data’, Trends in the Development of Sci. and Education, (84-2), pp. 60–64 (in Russ.). doi: 10.18411/trnio-04-2022-61.
5. Sharma, S., Sharma, S., Athaiya, A. (2020) ‘Activation functions in neural networks’, IJEAST, 4(12), pp. 310–316. doi: 10.33564/ijeast.2020.v04i12.054.
6. Bogdanov, P.Yu., Kraeva, E.V., Verevkin, S.A., Poymanova, E.D., Tatarnikova, T.M. (2021) ‘Software environ-ments for studying the basics of neural networks’, Software & Systems, 34(1), pp. 145–150 (in Russ.). doi: 10.15827/0236-235X.133.145-150.
7. Tariq, R. (2016) Make Your Own Neural Network. CreateSpace Publ., 223 p. (Russ. ed.: (2017) Moscow, 272 p.).
8. Macpherson, T., Matsumoto, M., Gomi, H., Morimoto, J., Uchibe, E., Hikida, T. (2021) ‘Parallel and hierarchical neural mechanisms for adaptive and predictive behavioral control’, Neural Networks, 144, pp. 507–521. doi: 10.1016/ j.neunet.2021.09.009.
9. Yu, S., Jiang, F., Li, L., Xie, Y. (2017) ‘CNN-GRNN for image sharpness assessment’, in LNIP. Proc. CNN, 10116, pp. 50–61. doi: 10.1007/978-3-319-54407-6_4.
10. Krutikov, A.K. (2018) ‘Forecasting sports results in individual sports using a generalized regression neural net-work’, Young Scientist, (12), pp. 22–26 (in Russ.).


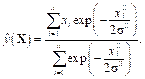 (5)
(5)

