Journal influence
Bookmark
Next issue
Method of an estimation of probability of acceptance of erroneous decisions at the discriminant analysis of transport knots
The article was published in issue no. № 3, 2009Abstract:Using diskriminants models in transport nodes, it is sufficiently often bring about wrong decisions. So finding to probability such mistakes exceedingly it is important, to term of the tense motion and manoeuvre of the transport units particularly. The method finding happens in work to probability such mistake and their estimations.
Аннотация:Применение дискриминационных моделей при организации процедур управления в транспортных узлах достаточно часто приводит к ошибочным решениям. Поэтому нахождение вероятности таких ошибок чрезвычайно важно, особенно в условиях напряженного движения и маневров транспортных единиц на ограниченном пространстве акваторий, терминалов. В работе приводится метод нахождения вероятности таких ошибок и их оценки.
| Authors: (tmp@nwpi.ru) - , Ph.D | |
| Keywords: system, mistake (error), probability, mathematical model, transport |
|
| Page views: 11667 |
Print version Full issue in PDF (4.21Mb) |
Применение дискриминационной модели в управлении транспортными узлами (ТУ) в некоторых случаях может дать ошибочное решение. Это вытекает из самого характера моделей данного типа. Такие ошибки опасны тем, что могут привести к неадекватным решениям по управлению грузовыми операциями на акваториях, терминалах, станциях, грузовых площадках и т.д. По характеру функционирования они сами по себе являются объектами повышенной техногенной и экологической опасности. Если в этих условиях к указанным ошибкам добавить ошибки модели управления такого рода объектами, процесс принятия решений может оказаться неадекватным уже на первых шагах анализа и прогнозирования состояния объекта (ТУ) и вызвать нарушения в переработке груза. Это приведет, в свою очередь, к накоплению товара, нарушению работы ТУ, вызовет скопление подвижного состава всех видов транспорта в данном ТУ. Поэтому нахождение и оценка вероятности таких ошибочных решений чрезвычайно важны, особенно в условиях напряженного движения и маневров транспортных единиц на ограниченных пространствах ТУ. Процесс управления ТУ рассматривается как единая процедура поддержки принятия решений взаимосвязанных подсистем выгрузки, переработки, хранения и погрузки товара для минимизации стоимости обработки груза в данном ТУ. Иными словами, управление в ТУ реализует схему подготовки и принятия решения по управлению для многомерных систем. Отсюда и постановка задачи оценки принятия ошибочных решений. Для двух многомерных систем
где
что известно как линейная дискриминационная функция (ЛДФ). Пусть В случае с ЛДФ
где F – дистрибуанта функции нормального распределения; Для одномерной системы
Оптимальным правилом решения, минимизирующим риск по Байесу [2, 4], будет утверждение: классифицируй наблюдение x в систему p1, если Подставляя случайную переменную X вместо наблюдения в правой части равенства (3), получаем соотношение
Произведя преобразования в (6) и принимая
Если
Если
Распределение T является линейной функцией смещенного распределения Если
Если
Отсюда
где Рассматривая функцию плотности смещенного распределения c2, вероятность (3) определится из следующего выражения:
Подобным образом
где Принимая алгоритмы, описанные в работах [3, 4], можно вычислить интегралы в равенствах (15) и (16) для любой группы параметров [3]. Более общим случаем поставленной задачи являются определение и оценка вероятностей ошибочных классификаций в случае многомерных нормальных систем. Для двух многомерных систем
Оптимальное правило решения, минимизирующее риск по Байесу, следующее: классифицируй наблюдение x в систему
в противном случае – в Подставляя многомерную случайную переменную X вместо наблюдения x в равенство (17) и принимая
получаем
Если
j=1, …, p. Если
j=1, …, p. Поскольку матрицы S1 и S2 диагональные, то X1, …, Xp независимы. Поэтому квадраты выражений (20) являются случайными переменными со смещенными распределениями c2, с одной степенью свободы и параметром смещения вида
j=1, …, p. Отсюда случайная переменная T является линейной комбинацией независимых случайных переменных со смещенным распределением c2. Патнайк [1] считал, что распределение линейной комбинации случайных переменных со смещенным распределением c2 может быть аппроксимировано многомерным центральным распределением Пусть где
В то же время функция
Дисперсию для W рассчитываем как вторую производную функции
Более того, Сравнивая E(W) и
и Аппроксимируя распределение W, определенное примером (23) через
Подставляя в равенства (28) и (29)
получим n и c. Подобным образом, когда
Подставляя в равенства (28) и (29)
Предложенный метод был успешно применен и внедрен в практику организации процессов управления в транспортной фирме BAFTRANS (Польша), что снизило ежедневные издержки обработки груза в ТУ на 12 %. Литература 1. Anderson T.W. An Introduction to Multivariate Statistical Analysis. Wilay, New York, 1958. 2. Kubicki J., Miklinska J., Urban-Popiolek I. Transport Miedzynarodowy Multimodalne Systemy Transportowe. Gdynia. 2000. 3. Арефьев И.Б., Пасевич В. Управляемая модель транспортного узла на базе распределения Гаусса. СПб: ГУВК, 2001. С. 37–40. 4. Маслов Е.П. Применение теории статистических решений к задачам оценки параметров объекта // Автоматика и телемеханика. 1963. № 10. С. 1338–1350. |
| Permanent link: http://swsys.ru/index.php?page=article&id=2328&lang=en |
Print version Full issue in PDF (4.21Mb) |
| The article was published in issue no. № 3, 2009 |
Perhaps, you might be interested in the following articles of similar topics:
- Методы анализа функциональных моделей
- Некоторые технологические аспекты создания учебно-тренировочных средств подготовки командиров и специалистов Военно-морского флота
- Задача определения группы риска для однородных транспортных узлов
- Архитектура системы информационно-имитационного моделирования поддержки жизненного цикла ИТ-инфраструктуры
- Программа диагностики заболеваний
Back to the list of articles
 дискриминационную функцию можно записать в виде
дискриминационную функцию можно записать в виде , (1)
, (1) – вектор средних;
– вектор средних;  – дополнительно определенная матрица дисперсий для i=1,2. Эта функция известна как квадратичная дискриминационная функция (КДФ), представляющая функцию двух форм, когда S1=S2=S, по выражению (1) она редуцируется в функцию
– дополнительно определенная матрица дисперсий для i=1,2. Эта функция известна как квадратичная дискриминационная функция (КДФ), представляющая функцию двух форм, когда S1=S2=S, по выражению (1) она редуцируется в функцию , (2)
, (2) означает вероятность классифицирования наблюдаемого вектора в
означает вероятность классифицирования наблюдаемого вектора в 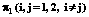 . Тогда расчет этих вероятностей требует данных распределения для КДФ и распределения для ЛДФ. Определение вероятности ошибочных классификаций описано в работах [1, 2].
. Тогда расчет этих вероятностей требует данных распределения для КДФ и распределения для ЛДФ. Определение вероятности ошибочных классификаций описано в работах [1, 2]. , когда
, когда  , и
, и  , когда
, когда  , где
, где  – расстояние Махалановича между двумя многомерными нормальными распределениями. В этом случае известны точные выражения для ошибочных классифицируемых систем [3].
– расстояние Махалановича между двумя многомерными нормальными распределениями. В этом случае известны точные выражения для ошибочных классифицируемых систем [3]. , где
, где  , (3)
, (3) , где
, где  , (4)
, (4) (q1 – априорная вероятность того, что наблюдения pi верны; Cij – затраты). В случае с КДФ распределение случайной переменной T неизвестно. Поэтому точные выражения для классификаций не определены. Рассмотрим определение ошибочных классификаций для одномерной нормальной системы.
(q1 – априорная вероятность того, что наблюдения pi верны; Cij – затраты). В случае с КДФ распределение случайной переменной T неизвестно. Поэтому точные выражения для классификаций не определены. Рассмотрим определение ошибочных классификаций для одномерной нормальной системы. и
и  , а также для данного наблюдения x КДФ имеет вид
, а также для данного наблюдения x КДФ имеет вид . (5)
. (5)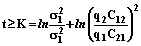 , в противном случае – в систему p1.
, в противном случае – в систему p1. . (6)
. (6) , получим
, получим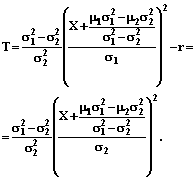 (7)
(7)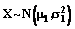 , тогда
, тогда . (8)
. (8) , тогда
, тогда . (9)
. (9)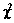 с одной степенью свободы и параметром смещения, зависящим от распределения случайной переменной X.
с одной степенью свободы и параметром смещения, зависящим от распределения случайной переменной X. , то
, то . (10)
. (10) . (11)
. (11)
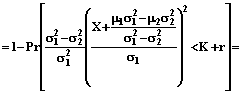
 , (12)
, (12) . (13)
. (13) . (14)
. (14) , (15)
, (15) . (16)
. (16) и
и 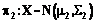 , где
, где  и
и  являются диагональными матрицами с диагональными элементами
являются диагональными матрицами с диагональными элементами  и векторами средних
и векторами средних 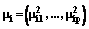 , i=1, 2, КДФ для наблюдаемого вектора имеет вид
, i=1, 2, КДФ для наблюдаемого вектора имеет вид . (17)
. (17)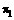 при
при  , где
, где , (18)
, (18)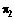 .
. , (19)
, (19) (20)
(20) и
и  , а также
, а также , (21)
, (21) и
и  , а также
, а также , (22)
, (22) и
и  , (23)
, (23) с n степенями свободы. Если принять
с n степенями свободы. Если принять 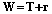 , то параметры n и c могут быть оценены путем сравнения первых двух моментов W и
, то параметры n и c могут быть оценены путем сравнения первых двух моментов W и 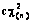 , где r, определяемое из (19), является постоянным.
, где r, определяемое из (19), является постоянным. , (24)
, (24) и
и  – известные постоянные (функции параметров двух многомерных нормальных распределений). Тогда X1,…,Xp будут одномерными случайными переменными с нормальными распределениями. Поэтому для каждой j Xj+bj является смещенным распределением c2 с одной степенью свободы и параметром смещения
– известные постоянные (функции параметров двух многомерных нормальных распределений). Тогда X1,…,Xp будут одномерными случайными переменными с нормальными распределениями. Поэтому для каждой j Xj+bj является смещенным распределением c2 с одной степенью свободы и параметром смещения 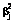 . Заметим, что зависимость
. Заметим, что зависимость 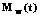 , определяющая моменты относительно W, имеет вид
, определяющая моменты относительно W, имеет вид (25)
(25) , создающая полуинварианты, будет натуральным логарифмом функций
, создающая полуинварианты, будет натуральным логарифмом функций 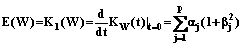 . (26)
. (26) (27)
(27) и
и  .
.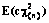 , а также
, а также  и
и  и вычисляя систему выражений относительно n и c, получим
и вычисляя систему выражений относительно n и c, получим (28)
(28) . (29)
. (29)
 , если c>0. (30)
, если c>0. (30) и
и  ,
, , выразим
, выразим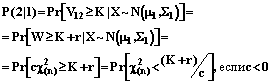
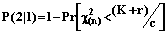 , если c>0. (31)
, если c>0. (31)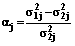 и
и  , получим n и c.
, получим n и c.