Journal influence
Bookmark
Next issue
The homogeneity analysis application to visualize and analyse bibliometrics and scientometrics data
The article was published in issue no. № 3, 2013 [ pp. 169-174 ]Abstract:The ensembles of trees, especially random forest have proved themselves to produce accurate predictions for solving regression and classification tasks. Perhaps unjustified, the main criticism of this approach is that these methods act as black boxes and do not provide additional information on the objects that are not participating in the training set. This paper considers a multi-class classification and shows that the homogeneity analysis used mainly in psychometrics can be used to provide effective visualization of the ensemble of trees, including visualization of the new observations that were not included in the training set. Observations and rules (nodes) of the ensemble of trees are placed in a bipartite graph connecting each observation with all the rules (nodes) that satisfies it. The location of the graph in this case is chosen according to minimizing the sum of edges lengths squares with certain limitations.
Аннотация:Для составления очень точных прогнозов при решении задач регрессии и классификации доказали свою состоятельность ансамбли деревьев, в особенности случайный лес. Основная, возможно, необоснованная критика этого подхода состоит в том, что данные методы действуют как черные ящики и не дают дополнительной информации относительно объектов, не участвовавших в обучающей выборке. В данной работе рассмотрена многоклассовая классификация и показано, что анализ однородности, который используется главным образом в психометрии, может быть применен для обеспечения эффективной визуализации ансамбля деревьев, в том числе визуализации новых наблюдений, не вошедших в обучающую выборку. Наблюдения и правила (узлы) ансамбля деревьев помещены в двудольный граф, соединяющий каждое наблюдение со всеми правилами (узлами), которым оно удовлетворяет. Расположение графа в этом случае выбирается согласно минимизации суммы квадратов длин ребер при определенных ограничениях.
| Authors: (aburilin@naumen.ru) - , Russia, (rgordeev@naumen.ru) - , Russia, Ph.D | |
| Keywords: visualization of graphs, homogeneity analysis, classification |
|
| Page views: 11631 |
Print version Full issue in PDF (13.63Mb) Download the cover in PDF (1.39Мб) |
В данной работе рассматривается проблема классификации данных и их визуального представления, а также предложен эффективный алгоритм, позволяющий значительно сократить количество вычислений, требуемых при малых изменениях анализируемых данных, возникающих в связи с добавлением или удалением какой-либо информации. Для многоклассовой классификации с K классами положим, что (X1, Y1), …, (Xn, Yn) – n наблюдений прогнозирующей переменной XÎX, а YÎ{1, …, K} – переменная ответа класса. Прогнозирующая переменная X является вектором размерности p и может содержать непрерывные или факторные переменные. Визуализация малоразмерных вложений данных может принимать различные формы: от неконтролируемого обучения до контролируемого уменьшения размерности или малоразмерных вложений данных, таких как анализ соседних компонентов [1] и схожих методов [2]. Однако авторы преследуют несколько иные цели: рассмотреть существующий алгоритм, точнее, класс алгоритмов, включающих случайный лес и вложенные деревья классификации, и разработать эффективные методы визуализации для членов этого класса. Ансамбли деревьев показали, что могут делать достаточно точные прогнозы, а случайный лес – возможно, один из лучших самообучающихся машинных алгоритмов в том смысле, что точность его предсказаний очень близка к истинному значению даже без особой настройки параметров. Рассмотрим случайный лес [3], вложенные деревья решений [4] и некоторые новые методы, например ансамбли правил [5]. Некоторые из существующих работ по визуализации деревьев [6] и ансамблей деревьев были всесторонне освещены в [7] и включают исследование рельефных графиков и графиков слежения, используемых, например, для определения устойчивости деревьев и переменных, выбранных в качестве критерия классификации. Так называемые матрицы близости часто используются для маломерных вложений наблюдений в классификации [3, 8, 9]. Вопросы неконтролируемого обучения с применением случайного леса рассмотрены в работе [10]. Каждая запись в матрице близости отражает долю деревьев в ансамбле, для которого пара наблюдений находится в одном и том же узле. Недостатком указанных методов визуализации является то, что исходные узлы дерева не отображаются, поскольку происходит потеря информации за счет агрегации в матрице близости. Кроме того, это затрудняет добавление новых наблюдений. В данной работе авторы будут применять методы анализа однородности для визуализации ансамблей деревьев. В этом подходе наблюдения и правила (узлы) формируют двудольный граф. Минимизация квадратов длин ребер в таком графе приводит к очень интересным малоразмерным проекциям данных. Размещение правил (узлов) и наблюдений на одном графике позволяет лучше интерпретировать проекции, а также точнее определять границы классов и отражать прогнозирование используемого ансамбля деревьев. Если количество классов классификации мало, можно показать, что обычное правило классификации ближайшего соседа для малоразмерных вложений данных позволяет производить прогнозирование с точностью, аналогичной точности прогнозирования при использовании случайного леса. В данном исследовании применяется метод анализа однородности для визуализации больших массивов наблюдений и правил на одном графике. Анализ однородности Матрица индикаторов. Анализ однородности был разработан в прикладных науках для исследования и прогнозирования социальных процессов и визуального представления данных с факторными переменными. Положим, что есть f факторных переменных h=1, …, f, каждая с уровнем фактора lh. Данные могут быть представлены в виде бинарной матрицы, если закодировать каждую из h=1, …, f переменных в виде n´lh матрицы бинарного индикатора G(h), в которой k-я колонка содержит 1 для всех наблюдений, имеющих уровень фактора k для переменной h. Эти матрицы могут быть объединены в матрицу n´m G=(G(1), …, G(f)), где m=Shlh – общее количество фиктивных переменных. Каждый из листьев дерева может быть представлен бинарной переменной, индикатором, в котором 1 означает, что наблюдение попадает в лист дерева, 0 – не попадает. Рассматривая листья как обобщенные фиктивные переменные, можно аналогично построить матрицу индикаторов G для ансамблей деревьев. Для данного ансамбля деревьев с общим количеством узлов m пусть листья Pj будут гиперплоскостями пространства X, соответствующими листу j, j=1, …, m. Наблюдение попадает в лист Pj тогда и только тогда, когда XiÎPj. Результаты ансамбля деревьев с m листьями во всех деревьях можно объединить в матрицу индикаторов G размерности n´m, где Gij=1, если i-е наблюдение попадает в j-й лист, и 0 в противном случае:
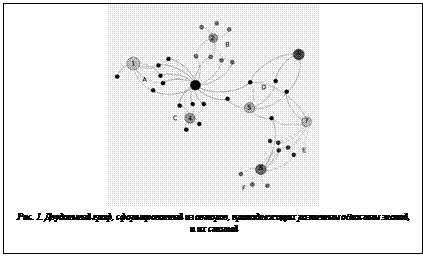
Двудольный граф и анализ однородности. Анализ однородности можно рассматривать как формирование двудольного графа, в котором каждое из n наблюдений и каждое из m правил или фиктивных переменных представлены узлом графа. Между наблюдением и правилом (узлом) существует ребро тогда и только тогда, когда наблюдение удовлетворяет правилу. Другими словами, между наблюдением i и правилом j существует ребро тогда и только тогда, когда Gij=1. Таким образом, нужно расположить наблюдение как можно ближе ко всем правилам, которые его содержат. И, наоборот, правило должно находиться как можно ближе к наблюдению, которое оно содержит. На рисунке 1 представлен пример отображения выборки авторов, принадлежащих различным областям знаний, и их статей. В данном случае статьи (малые узлы графа) являются наблюдениями, а авторы (большие узлы графа) – правилами. Некоторые авторы могут иметь совместные статьи, то есть при классификации статей могут формироваться группы, которые не только отражают принадлежность той или иной статьи к определенному роду знаний, но и показывают связи между различными видами знаний. Так, например, фиолетовым (цифра 3) и желтым (маркер 1) отмечены соответственно математик и физик; таким образом определено, что виды знаний весьма тесно связаны, а совместные статьи этих авторов образуют отдельный кластер, который ошибочно содержит и отдельную статью по физике. Анализ однородности пытается минимизировать сумму квадратов длин всех ребер. На картинке представлен граф при фиксированном положении правил. Каждая статья располагается в центре относительно всех правил, которые к ней применяются. Цвет статей соответствует различным классам. Физико-математические статьи, например, обозначаются красным (литера A), статьи на стыке информатики и математики – зеленым (литера C). Пусть U – матрица размером n´q, содержащая координаты n наблюдений во вложении размерности q, R – матрица m´q проецируемых правил. Обозначим через Ui i-ю строку матрицы U, а через Rj j-ю строку матрицы R. Анализ однородности выбирает проекцию, минимизируя квадраты длин ребер: Пусть en – n-мерная колонка-вектор, содержащая одни единицы, а 1q – q-мерная единичная матрица. Чтобы избежать тривиальных решений, дополнительно накладываются ограничения [11] вида UTWU=1q, (2) eTnU=0, (3) где W – положительно определенная весовая матрица. Таким образом, анализ однородности соответствует нахождению вложения размерности q (где q обычно равно 2) как наблюдений, так и правил, таких, что сумма квадратов длин ребер является минимальной. Далее будем взвешивать выборки количеством правил, с которыми они связаны, таким образом, W будет диагональной матрицей с элементами Wii=SjGij, поэтому W=diag(GGT) является диагональной частью GGT. В стандартном анализе однородности каждая выборка является частью точно такого же количества правил, поскольку соответствует уровням фактора, и весовая матрица W=f1n, таким образом, будет единичной матрицей, умноженной на число f факторной переменной. Для большинства ансамблей деревьев также справедливо, что W=T1n является диагональной матрицей, поскольку каждое наблюдение попадает в такое же количество T листьев, где T – количество деревьев в ансамбле. Основные результаты Отображение правил. Если координаты U наблюдений остаются постоянными, то расположения правил R в задаче (1) при ограничениях (2) могут быть легко найдены, поскольку ограничения не зависят от R. Каждая проекция правила Rj, j=1, …, m, находится в центре относительно всех наблюдений, которые содержит правило:
где diag(M) – диагональная часть матрицы M, в которой все элементы, не принадлежащие диагонали, равны 0. Значения матрицы U могут быть найдены методом наименьших квадратов или путем решения задачи с собственными значениями. Задача оптимизации (1) при ограничениях (2) может быть решена либо оптимизацией позиций U для n реализаций, либо оптимизацией позиций R для m правил, при этом в каждом случае остальные параметры остаются неизменными. Опти- мизация относительно позиций правил R при заданных фиксированных позициях U реализаций решена в (4). Оптимизация относительно U при ограничениях (2) решается методом наименьших квадратов аналогично (4): U=diag(GGT)-1GR, (5) помещая каждую реализацию в центр всех правил, которые ее содержат [12]. В отличие от следующего подхода, основан- ного на вычислении собственных значений, вычисления состоят только из умножения матриц. А поскольку G в большинстве случаев является разряженной матрицей, это может значительно улучшить эффективность вычислений. Целевая функция задачи (1) может быть альтернативно записана в виде
где tr(M) – след матрицы M. Обозначим Тогда исходная задача может быть сведена к задаче вида
при ограничениях Далее, используя разложение по собственным векторам и (4), получим решение:
где V=(v1, …, vq) – матрица, состоящая из первых q собственных векторов матрицы
Фиксированные позиции правил и новые наблюдения. После получения раскладки графа (8) упрощается второй шаг и фиксируется положение правил в точках полученных решений. В этом случае анализ однородности будет иметь очень полезное свойство: можно элементарно добавлять новые наблюдения на график без пересчета всего решения. Минимизировать сумму квадратов длин ребер (1) при фиксированных позициях правил весьма просто: наблюдение помещается в центр всех правил, которые к нему применяются. В матричном виде решение выглядит так:
Простой пример приведен на рисунке 1. На нем представлены статьи (наблюдения) и авторы (правила), полученные на основе анализа структуры данных системы цитирования elibrary.ru. Правила являются бинарными индикаторами, отражающими одну или несколько характеристических черт (в данном исследовании это авторство статьи). Для размещения наблюдений предлагается следующий подход. 1. Находим положение правил, минимизируя сумму квадратов длин ребер, при ограничениях (2) и (3). 2. Фиксируем положение правил и размещаем все наблюдения U, минимизируя снова сумму квадратов длин ребер: каждое наблюдение размещается в центре всех правил, которые к нему применяются, используя (9). 3. Добавляем новое наблюдение и вычисляем его расположение, используя (9). В примере, приведенном на рисунке 2, показано предсказание новых наблюдений в двухмерных проекциях. Раскрашенные наблюдения соответствуют обучающим наблюдениям с известными кодами цвета (класса области знаний). Светло-фиолетовым (обозначено литерой A’) изображена статья по физике, авторами которой являются физик, математик и информатик. Статья при этом правильно классифицирована и отнесена к области знаний «физика», поскольку это ближайшая обучающая группа. Справа аналогично классифицируется изображенная серым узлом (обозначено литерой E’) статья по медицине, написанная медиком, специалистом в области ИТ и биологом. Однако она была неверно отнесена к области знаний «химия» (розовый цвет, группа E). Пример Применим анализ однородности для оценки действий экспертов, рецензирующих статьи в научных журналах. И, кроме того, попробуем проанализировать некоторые другие интересные характеристики, полученные в ходе эксперимента. Данные о результатах экспертизы статей, принимаемых в рецензируемые журналы по астрофизике, были собраны Нури и Роландом в 2002–2006 годах. Всего получена информация о 5 745 оценках статей 696 экспертами. При каждой оценке возможен один из трех вариантов: оценить положительно, оценить отрицательно, отправить на доработку.
Все эксперты принадлежали одному из восьми научных центров: первый будем обозначать светло-голубым, второй – темно-синим, третий – желтым, четвертый – зеленым, пятый – красным, шестой – оранжевым, седьмой – коричневым, восьмой – черным. Классификатор – случайный лес со 100 деревьями и параметрами, настроенными на обучающей выборке. Принадлежность эксперта тому или иному научному центру определяется при помощи случайного леса с ошибкой примерно в 10 %. Двухмерные вложения выбраны для выявления связей между научными центрами и для определения экспертов, ведущих себя отлично от своих коллег. Многомерное шкалирование. Для визуализации результатов анализа, полученных при помощи случайного леса, обычно применяют многомерное шкалирование близостей [3, 8]. Близость двух наблюдений определяется как соотношение деревьев в случайном лесе, для которого оба наблюдения попадают в листовой узел. Матрица близостей в наших обозначениях может быть вычислена при помощи следующего выражения: T–1GGT, где T – количество деревьев в ансамбле. Расстояние, определяемое как 1, меньше, чем близость. Тогда матрица расстояний вычисляется при помощи выражения 1n–T–1GGT или монотонного преобразования, такого, как квадратный корень [10]. Здесь используется неметрическое многомерное шкалирование, а именно isoMDS [13–15], которое делает результаты инвариантными относительно любого монотонного преобразования расстояний. MDS генерирует двухмерные вложения для всех наблюдений, в данном случае экспертов, которые можно видеть слева на рисунке 3. Хотя это дает представление о близости между институтами, все же научные центры не располагаются, как когерентные блоки, и особенно это заметно на экспертах из 7-го и 8-го научных центров (черный и коричневый), которые весьма широко разбросаны.
Однако даже эти результаты дают весьма интересную картину. Так, можно сказать, что эксперты из институтов 2, 3, 7, 8 примерно одинаково оценивают все статьи, в то время как эксперты из 4-го и 6-го институтов некоторые статьи оценивают одинаково, а относительно других статей их мнения расходятся. На основании изложенного отметим, что метод однородности для визуализации и классификации данных заключается в вычислении начальных расположений правил на основе обучающей выборки и в формировании начальных групп наблюдений на базе метода наименьших квадратов. Далее фиксируется расположение правил, отно- сительно которых располагаются поступающие новые наблюдения. Классификация новых наблюдений производится на основе принципа «ближайшего соседа» по отношению к классам наблюдений, сформированным обучающими данными. Данный подход позволяет избежать полного пересчета всей модели при добавлении в нее новых наблюдений и увеличить скорость работы алгоритма. Возможности подхода продемонстрированы на модельном примере, оценивающем связи институтов на основе действий экспертов, рецензирующих статьи. Литература 1. Goldberger J., Roweis S., Hinton G. and Salakhutdinov R., Neighbourhood Components Analysis, in Advances in Neural Inf. Proc. Syst., 2005, Vol. 17, pp. 513–520. 2. Sugiyama M., Dimensionality Reduction of Multimodal Labeled Data by Local Fisher Discriminant Analysis, Journ. of Machine Learning Research, 2007, no. 8, 1061 p. 3. Breiman L., Random Forests, Machine Learning, 2001, no. 45, pp. 5–32. 4. Breiman L., Bagging Predictors, Machine Learning, 1996, no. 24, pp. 123–140. 5. Friedman J. and Popescu B., Predictive Learning via Rule Ensembles, The Annals of Applied Statistics, 2008, no. 2, pp. 916–954. 6. Breiman L., Friedman J., Olshen R., and Stone C., Classification and Regression Trees, Belmont: Wadsworth, 1984. 7. Urbanek S., Visualizing Trees and Forests, in Handbook of Data Visualization, Berlin, Heidelberg: Spinger, 2008, pp. 243–264. 8. Liaw A. and Wiener M., Classication and Regression by RandomForest, R News, 2002, no. 2, pp. 18–22. 9. Lin Y. and Jeon Y., Random Forests and Adaptive Nearest Neighbors, Journ. of the American Statistical Association, 2006, no. 101, 578–590. 10. Shi T. and Horvath S., Unsupervised Learning With Random Forest Predictors, Journ. of Computational and Graphical Statistics, 2006, no. 15, pp. 118–138. 11. De Leeuw J. and Mair P., Homogeneity Analysis in R: The Package Homals, Journ. of Statistical Software, 2008, no. 31, pp. 1–21. 12. Michailidis G. and De Leeuw J., The Gifi System of Descriptive Multivariate Analysis, Statistical Science, 1998, no. 13 (4), pp. 307–336. 13. Borg I. and Groenen P., Modern Multidimensional Scaling: Theory and Applications, NY: Springer, 1997. 14. Kruskal J., Nonmetric Multidimensional Scaling: A Numerical Method, Psychometrika, 1964, no. 29, pp. 115–129. 15. Kruskal J. and Wish M., Multidimensional Scaling, Beverly Hills: Sage Publ., 1978. References 1. Goldberger J., Roweis S., Hinton G., Salakhutdinov R., Advances in Neural Inf. Proc. Syst., 2005, Vol. 17, pp. 513–520. 2. Sugiyama M., Journ. of Machine Learning Research, 2007, no. 8, 1061 p. 3. Breiman L., Machine Learning, 2001, no. 45, pp. 5–32. 4. Breiman L., Machine Learning, 1996, no. 24, pp. 123–140. 5. Friedman J., Popescu B., The Annals of Applied Statistics, 2008, no. 2, pp. 916–954. 6. Breiman L., Friedman J., Olshen R., Stone C., Classification and Regression Trees, Belmont, Wadsworth, 1984. 7. Urbanek S., Handbook of Data Visualization, Berlin, Heidelberg, Spinger, 2008, pp. 243–264. 8. Liaw A., Wiener M., R News, 2002, no. 2, pp. 18–22. 9. Lin Y., Jeon Y., Journ. of the American Statistical Association, 2006, no. 101, pp. 578–590. 10. Shi T., Horvath S., Journ. of Computational and Graphical Statistics, 2006, no. 15, pp. 118–138. 11. De Leeuw J., Mair P., Journ. of Statistical Software, 2008, no. 31, pp. 1–21. 12. Michailidis G., De Leeuw J., Statistical Science, 1998, no. 13 (4), pp. 307–336. 13. Borg I., Groenen P., Modern Multidimensional Scaling: Theory and Applications, NY, Springer, 1997. 14. Kruskal J., Psychometrika, 1964, no. 29, pp. 115–129. 15. Kruskal J., Wish M., Multidimensional Scaling, Beverly Hills, Sage Publ., 1978. |
| Permanent link: http://swsys.ru/index.php?page=article&id=3581&lang=en |
Print version Full issue in PDF (13.63Mb) Download the cover in PDF (1.39Мб) |
| The article was published in issue no. № 3, 2013 [ pp. 169-174 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Метод секционирования и его применение при классификации разнородной информации
- Разработка теоретических основ классификации и кластеризации нечетких признаков на основе теории категорий
- Кластеризация документов интеллектуального проектного репозитария на основе FCM-метода
- Инструментальная система для решения задач многокритериального выбора
- Задачи информационного поиска в рамках интеллектуальной распределенной программной системы информационной поддержки инноваций
Back to the list of articles

 Эта матрица очень похожа на матрицу индикаторов анализа однородности. Построковая сумма матрицы G идентична числу F факторных переменных анализа однородности, более того, построковая сумма G для ансамблей деревьев равна числу деревьев, поскольку каждое наблюдение попадает только один раз в лист в каждом дереве. Далее не будем считать построковую сумму постоянной, это позволит сделать некоторые обобщения без чрезмерного усложнения обозначений и вычислений. Единственное предположение заключается в том, что суммы по строкам и колонкам матрицы G строго положительны, то есть каждое наблюдение попадает по крайней мере в один узел, а каждый узел содержит по крайней мере одно наблюдение. Кроме того, будем полагать, что корневой узел, содержащий все наблюдения, входит в набор правил. Это гарантирует, что двудольный граф, соответствующий G, является связанным.
Эта матрица очень похожа на матрицу индикаторов анализа однородности. Построковая сумма матрицы G идентична числу F факторных переменных анализа однородности, более того, построковая сумма G для ансамблей деревьев равна числу деревьев, поскольку каждое наблюдение попадает только один раз в лист в каждом дереве. Далее не будем считать построковую сумму постоянной, это позволит сделать некоторые обобщения без чрезмерного усложнения обозначений и вычислений. Единственное предположение заключается в том, что суммы по строкам и колонкам матрицы G строго положительны, то есть каждое наблюдение попадает по крайней мере в один узел, а каждый узел содержит по крайней мере одно наблюдение. Кроме того, будем полагать, что корневой узел, содержащий все наблюдения, входит в набор правил. Это гарантирует, что двудольный граф, соответствующий G, является связанным. . (1)
. (1) , R=diag(GTG)-1GTU, (4)
, R=diag(GTG)-1GTU, (4)

 ,
,  .
. (6)
(6) ,
, 
 (7)
(7) , (8)
, (8) .
. . (9)
. (9) При анализе этих данных встает вопрос о том, можно ли установить связь между оценкой статьи и принадлежностью эксперта определенному научному центру. Это позволит сделать ряд определенных выводов, касающихся предвзятой оценки своих коллег, насколько одинаково оценивают статьи эксперты из одного научного центра, существуют ли среди экспертов определенные подгруппы. Также необходимо выяснить, есть ли связь между национальностью эксперта и его оценками статей.
При анализе этих данных встает вопрос о том, можно ли установить связь между оценкой статьи и принадлежностью эксперта определенному научному центру. Это позволит сделать ряд определенных выводов, касающихся предвзятой оценки своих коллег, насколько одинаково оценивают статьи эксперты из одного научного центра, существуют ли среди экспертов определенные подгруппы. Также необходимо выяснить, есть ли связь между национальностью эксперта и его оценками статей.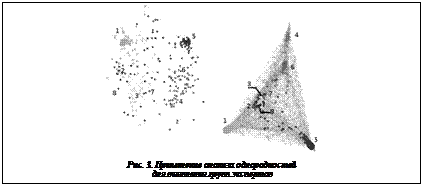 Анализ однородности. Справа на рисунке 3 представлены результаты обработки тех же данных при помощи анализа однородности. При этом G является матрицей размерности n´m, в которой каждый из m столбцов соответствует листовому узлу случайного леса. Значение 0 соответствует случаю, когда эксперт не попал в лист, 1 – попал. Теперь заметно, что все научные центры имеют свои точки притяжения и располагаются более компактно, формируя треугольник, как показано на рисунке 3 справа. На нем отчетливо видны достаточно сильные взаимосвязи некоторых из научных центров. При использовании этого подхода неверная классификация составляет примерно 19 % и есть еще над чем работать (для случая использования метода ближайшего соседа в двухмерных вложениях).
Анализ однородности. Справа на рисунке 3 представлены результаты обработки тех же данных при помощи анализа однородности. При этом G является матрицей размерности n´m, в которой каждый из m столбцов соответствует листовому узлу случайного леса. Значение 0 соответствует случаю, когда эксперт не попал в лист, 1 – попал. Теперь заметно, что все научные центры имеют свои точки притяжения и располагаются более компактно, формируя треугольник, как показано на рисунке 3 справа. На нем отчетливо видны достаточно сильные взаимосвязи некоторых из научных центров. При использовании этого подхода неверная классификация составляет примерно 19 % и есть еще над чем работать (для случая использования метода ближайшего соседа в двухмерных вложениях).