Задача моделирования процесса растворения твердых тел актуальна во многих областях прикладной науки, например, в фармацевтике для прогнозирования кинетики высвобождения веществ из лекарственных форм или в сельском хозяйстве для определения потенциальных свойств композиций, применяемых в качестве удобрений. Моделирование физико-химических процессов на микроуровне является многопараметрической, трудноформализуемой и ресурсоемкой задачей [1], решение которой требует разработки новых подходов к моделированию и организации вычислений.
Существующие математические модели растворения можно разделить на две основные группы: детерминированные и стохастические. Обе группы исследуют целую популяцию частиц и описывают изменение концентрации во времени. Детерминированные модели чаще всего основаны на дифференциальных уравнениях и плохо подходят для описания процесса растворения многокомпонентных твердых тел и тел со сложной внутренней структурой из-за большого количества факторов, которые необходимо учесть и описать уравнениями.
Авторами предложена модель растворения твердых тел на основе клеточных автоматов, которая позволяет совместить преимущества стохастического и детерминированного подходов и успешно реализовать алгоритм расчета с использованием высокопроизводительных параллельных вычислений.
В статье также рассмотрен разработанный программный комплекс, позволяющий моделировать процесс растворения полимерных нанокомпозитов, содержащих жесткие и мягкие включения, исходя из начального состава твердого тела, геометрической формы и внешних воздействий (температура среды растворения и скорость движения жидкой фазы вокруг твердой).
Описание модели клеточного автомата
Клеточный автомат представляет собой набор кубических полей с линейным размером N клеток. В математической модели приняты следующие допущения:
– система представляется как совокупность полей, состоящих из кубических клеток;
– расчет идет итеративно, процессы, протекающие на каждой итерации, принимаются как протекающие в один момент времени;
– на каждом поле рассматриваются только одно вещество и среда растворения (растворитель);
– поля имеют открытые границы, на каждой итерации вещество из граничных клеток удаляется;
– клетка описывается тремя характеристиками: типом вещества, количеством вещества, находящегося в данной клетке, и агрегатным состоянием (жидкость или твердое вещество);
– растворяемые вещества или не влияют друг на друга, или скорость растворения одного вещества линейно зависит от концентрации другого;
– каждая клетка имеет шесть соседних клеток.
Состояние поля на следующей по времени итерации зависит только от состояния поля на предыдущей итерации. В связи с этим возможен параллельный расчет для каждой клетки поля.
Линейный размер одной клетки и полей клеточного автомата задается в качестве начальных условий. Экспериментально установлено, что он должен быть равным 10 мкм. Соответственно объем одной клетки составляет 10-15 м3.
Для каждого вещества определяется его максимально возможное количество, которое может содержаться в ячейке поля, исходя из объема клетки, плотности вещества и молекулярной массы вещества по формуле
 , (1)
, (1)
где vmax – максимальное количество вещества в одной клетке автомата в молях; l – линейный размер одной клетки; ρ – плотность вещества (при прессовании определяется экспериментально); M – молекулярная масса вещества.
Количество вещества, необходимого для приготовления насыщенного раствора данного вещества в объеме, равном объему одной клетки, рассчитывается исходя из концентрации насыщенного раствора вещества в заданном растворителе.
Концентрация насыщенного раствора определяется по справочным данным или экспериментально.
При расчетах принимается следующее допущение: если количество вещества в клетке находится в диапазоне от максимально возможного количества вещества до количества вещества, необходимого для насыщенного раствора в объеме клетки, то агрегатное состояние вещества в клетке принимается как твердое. Если количество вещества находится в диапазоне от количества вещества, необходимого для насыщенного раствора, до нуля, то агрегатное состояние вещества в клетке принимается как жидкость.
Для каждой клетки поля производится расчет процессов растворения твердого вещества в жидкой фазе, диффузии растворенного вещества за счет разности концентраций (по закону Фика), переноса нерастворимого вещества за счет внешних факторов (движение жидкой фазы).
Процесс растворения рассчитывается во всех клетках, имеющих агрегатное состояние твердое вещество, во все соседние клетки обратно пропорционально концентрациям растворяющегося вещества в них. Количество вещества, перешедшего в растворенное состояние, определяется по уравнению, позволяющему рассчитать изменение массы в клетке, из которого вещество растворяется:  (2)
(2)
где М – изменение массы твердого вещества; k – коэффициент растворения; F – поверхность растворения; Cнасыщ – концентрация насыщенного раствора. Наиболее общее уравнение для расчета коэффициента растворения k в аппаратах с мешалками получено на основе предположения, что решающую роль во внешнем массообмене выполняет разрушение пограничного слоя мелкомасштабными турбулентными пульсациями:
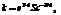 (3)
(3)
 (4)
(4)
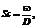 (5)
(5)
где e – удельная диссипация механической энергии; Sc – критерий Шмидта (диффузионный критерий Прандтля); N – мощность, затрачиваемая на перемешивание; G – масса перемешиваемой суспензии [2].
После расчета процесса растворения во всех возможных клетках, исходя из новых значений количества вещества в клетках, по правилам, описанным выше, определяется их новое агрегатное состояние. Расчет с помощью предлагаемого математического описания без ограничений реализуется с использованием приемов распараллеливания вычислений.
Расчет процесса диффузии осуществляется по уравнению Фика. В процессе расчета диффузии участвуют только те клетки, которые имеют агрегатное состояние жидкость. На основе предыдущих значений для каждой клетки, содержащей растворенное вещество, и ее новых соседей рассчитываются новые значения количества содержащегося в них вещества.
Такой расчет также без ограничений реализуется с использованием приемов распараллеливания вычислений.
Расчет процесса переноса вещества: случайным образом выбирается p процентов пар клеток, имеющих одно из следующих состояний:
– раствор вещества – раствор вещества;
– раствор вещества – растворитель;
– твердое нерастворимое вещество – растворитель;
– твердое нерастворимое вещество – раствор вещества.
Количество выбранных клеток является эмпирической величиной и подбирается на основе сравнения результатов моделирования с экспериментальными данными. На заключительной стадии происходит удаление вещества из граничных клеток клеточного автомата, что имитирует большой объем реальной системы.
После расчета итерации происходит проверка выполнения закона сохранения массы (количество вещества в системе совокупно с количеством удаленного из системы вещества должно быть постоянным). При необходимости сохраняется состояние поля для дальнейшей визуализации системы и возможности возобновить расчет при его прерывании. Расчет завершается при переходе всех клеток, содержащих растворимые вещества, из состояния твердое вещество в состояние раствор вещества.
Разработанная математическая модель может быть использована для проведения расчетов процесса растворения любых твердых тел. Количество веществ, из которых состоит твердое тело, не ограничено. Математическая модель позволяет получить не только конечные данные об исследуемом образце (значения водорастворимости, водопоглощения), но и динамику процесса растворения. Модель является развитием модели, описанной в [1].
Программная реализация
Разработанная модель легла в основу программного комплекса.
В него входят три модуля: подготовки начальных данных, расчета, визуализации и сравнения результатов.
Модуль подготовки начальных данных представляет собой визуальный интерфейс для задания начальных внутренней и внешней геометрий твердого тела, состава твердого тела и среды, внешних воздействий на твердое тело. Пользователь имеет возможность загрузить заранее сгенерированные внутренние структуры твердого тела, распределить компоненты случайно равномерно или в соответствии с некоторыми условиями. После задания начальных условий модуль генерирует файл, необходимый для модуля расчетов.
Модуль расчетов реализует алгоритм расчета системы с помощью вероятностного клеточного автомата с сохранением промежуточных данных и проверкой выполнения закона сохранения массы в системе.
Описание алгоритма расчета
Алгоритм расчета реализован с применением методов распараллеливания вычислений. Алгоритм включает три этапа, повторяющиеся итеративно: подготовка входных данных, сохранение и визуализация данных. Блок-схема работы программного комплекса, алгоритма расчета и схема распараллеливания представлены на рисунке.
На этапе подготовки данных пользователь задает следующие значения.
· Линейный размер и геометрическая форма растворяемого объекта.
· Внутренняя и внешняя структуры растворяемого объекта. Пользователь имеет возможность загрузить структуру матрицы твердого тела, если она заранее сгенерирована, или распределить вещества, из которых состоит растворяемый объект, случайно равномерно по всему объему объекта в соответствии с их массовыми долями. При задании внешней структуры (покрытия) пользователь имеет возможность указать толщину покрытия и количество слоев покрытия. Слои могут состоять из различных веществ, и растворяемый объект может содержать несколько слоев покрытия.
· Физико-химические свойства всех веществ, присутствующих в системе (плотность, молекулярная масса, коэффициент диффузии и т.д.).
· Внешние факторы, действующие на объект растворения (скорость оборотов мешалки, температура среды).
Далее происходит итеративный расчет трех указанных выше процессов.
 Модуль визуализации и сравнения результатов представляет собой интерфейс для графического отображения системы в 2D- и 3D-форматах, вывод графической информации о процессе растворения. Кроме этого, модуль позволяет сохранять состояния клеточного автомата в формат 3ds с целью использования для визуализации существующих программных комплексов (3D Max, Google SketchUp).
Модуль визуализации и сравнения результатов представляет собой интерфейс для графического отображения системы в 2D- и 3D-форматах, вывод графической информации о процессе растворения. Кроме этого, модуль позволяет сохранять состояния клеточного автомата в формат 3ds с целью использования для визуализации существующих программных комплексов (3D Max, Google SketchUp).
Программный комплекс реализован на платформах Microsoft .Net Framework 4.0/4.5 и Oracle Java Runtime с помощью языков программирования C# и Java. В качестве библиотеки для визуализации использовалась OpenGL. Модуль расчетов поддерживает параллельные вычисления с помощью технологии Microsoft Parallel.
Результаты расчетов и дальнейшее развитие программного комплекса
Были проведены моделирование и численное сравнение с экспериментальными данными процесса растворения полимерного нанокомпозита (ПНК). При моделировании приняты следующие допущения.
· ПНК содержит три компонента: жесткие включения (наполнитель), мягкие включения (модификатор), полимерную матрицу.
· Концентрация компонентов лежит в интервалах: жесткие включения – 75–80 % от общей массы, мягкие включения – 0–10 %, полимерная матрица – 10–25 %.
· ПНК рассматривается после отвердевания (не рассматривается переход из высоковязкого в твердое состояние).
На текущий момент были получены результаты численного моделирования системы, состоящей из трехкомпонентного твердого тела. Линейный размер клеточного автомата составил 500 клеток, всего клеток в системе – 375 миллионов. Время одного расчета – около 40 часов при конфигурации 2 Intel Xeon E2650 (4 физических ядра, 8 виртуальных ядер на 1 процессор), 32 ГБ RAM.
Расчет был проведен для образца следующего состава: жесткие включения – 75 %, мягкие включения – 5 %, полимерная матрица – 20 %.
В ходе расчета получены кинетика растворения и значение водорастворимости для данного образца, которое составило 3,7 мкг/мм3, что со- ответствует экспериментально измеренной величине.
Предполагается развитие данного программного продукта в двух основных направлениях: развитие и оптимизация кода программного модуля, отвечающего за процесс расчета с помощью клеточного автомата, и добавление новых моделируемых процессов.
Планируется реализация расчетного модуля с использованием технологии NVidia CUDA, которая позволяет производить расчет с использованием графических процессоров и добиться выдающейся производительности в задачах с преобладанием мелкозернистого параллелизма. Это даст возможность моделировать более сложные процессы и твердые тела, в том числе с нанокомпозитными включениями.
Планируется также расширение функциональных возможностей комплекса путем добавления в него новых клеточных автоматов для моделирования таких параметров твердых тел, как напряжение при сгибе, напряжение при растяжении и сжатии, микротвердость и другие.
Литература
1. Меньшутина Н.В., Иванов С.И., Шипилова Д.Д. Моделирование растворения твердых тел с помощью клеточных автоматов // Программные продукты и системы. 2012. № 1. С. 151–154.
2. Дытнерский Ю.И., Борисов Г.С., Брыков В.П. [и др.]. Основные процессы и аппараты химической технологии: пособие по проектированию. М.: Химия, 1991. 496 с.
3. Laaksonen T.J., Laaksonen H.M., Hirvonen J.T., Murtomäki L., Cellular automata model for drug release from binary matrix and reservoir polymeric devices, Biomaterials, 2009, April, Vol. 30, Iss. 10, pp. 1978–1987.
References
1. Menshutina N.V., Ivanov S.I., Shipilova D.D., Programmnye produkty i sistemy [Software & Systems], 2012, no. 1, pp. 151–154.
2. Dytnersky Yu.I., Borisov G.S., Brykov V.P., Osnovnye protsessy i apparaty khimicheskoy tekhnologii: posobie po proektirovaniyu [Basic processes and devices of chemical technology: design manual], 2nd ed., Moscow, Khimiya, 1991.
3. Laaksonen T.J., Laaksonen H.M., Hirvonen J.T., Murtomäki L., Biomaterials, 2009, Vol. 30, iss. 10, pp. 1978–1987.
 , (1)
, (1) (2)
(2)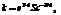 (3)
(3) (4)
(4)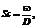 (5)
(5)
