Nowadays developments in the field of computer science are becoming increasingly important – data processing algorithms are hardware/firmware implemented. Neural networks, fuzzy logic, genetic algorithms and a number of other information technologies recently known only to a narrow circle of specialists, have become widely used in the last decade. Problems solved by information systems in most cases are reduced to a series of typical ones. They include [1] the following: classification of images, clustering, approximation of functions, forecast, optimization, associative memory, management.
So, problem management is complicated, in most cases it is necessary to solve a complex of tasks mentioned above in order to solve it.
In classical training rules for fuzzy neural networks the number of production rules, type of membership functions, fuzzy inference algorithm type, etc. is given a priori and does not change during the network training. In the case of an incorrect choice of these parameters fuzzy neural networks can be ineffective for automation. To avoid this situation it is better to apply adaptive algorithms (self-ogranization) of fuzzy neural networks which set up not only training parameters but also the structure of the network. A few basic principles of self-organization algorithms of fuzzy systems have been defined [1]: copying of training set; optimization of the number of production rules as a single parameter; overall optimization in the number of production rules and fuzzy network weights; gradually growing partitioning algorithm (Incremental Decomposition Algorithm).
The above stated algorithms are distinguished by very high requirements to computing resources. The procedure of parametric optimization search requires significant computational costs. In this regard, algorithms that do not require a repeated reset in case of removing or adding production rules are of value in terms of reducing computational complexity. Algorithms that belong to this type are stated below:
- reduction algorithms for fuzzy neural networks (reduction algorithms) [2];
- constructive algorithms for fuzzy neural networks (constructive algorithms) [3];
- fuzzy complementative adaptive algorithm of fuzzy inference [1].
The aim of this article is to develop scientific and technical solutions aimed at improving the quality and reliability of the automatic control of dynamic objects based on improving the adaptive algorithm of fuzzy neural networks functioning as part of intelligent automatic control systems (ACS).
Theoretical analysis of the intelligent ACS synthetics methodology [4] has led to the conclusion that the development and introduction of hybrid intelligent control systems that use dynamic intelligent database to convert generic concepts will allow to record specified quality parameters when exposed to uncontrollable external perturbations through intellectual correction of the system parameters.
We propose to put the solution of automatic control problems on a hybrid ACS, which implements a complex multi-dimensional functional transformation of the input vector according to the functioning adaptive algorithm. The developed structure of the lower level of intelligent ACS [4] contains an adaptive neuro-fuzzy system which performs functions of an emulator of a control object inverse dynamics.
In order to reduce the requirements for computational resources with the support of adaptive properties of the system it is necessary to develop a set of hardware and software for the intelligent ACS focused on swift corrections of production rules base structure of neuro-fuzzy emulators (NFE) of control objects inverse dynamics. Known developments of adaptive algorithms [1–3] operate in the error accumulation mode and are quite complex in terms of microprocessor-based devices implementation.
The Wang-Mendel network [5] with a modified form of adaptive algorithm [4] has been selected as the basic structure of neuro-fuzzy emulator.
Operation of the developed algorithm is based on the theory of sampling frequency and training frequency distribution [4]. In the theory of control systems with discrete time it is determined that the sampling time T is usually selected according to the following rule of thumb: the value must exceed the maximum frequency of the system. In traditional adaptive control systems parameters are adjusted once every sampling period. Thus the sampling rate and update rate are not separated.
With rational training of neuromorphic structures the basic work pace of the control system is distributed to additional ranges of training iterations with the condition that the sampling period is much higher than the time it takes to conduct one training iteration.
Start time of internal pace  is a variable value which is formed by the system based on time analysis
is a variable value which is formed by the system based on time analysis 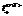 of the new list last creating per attributes (c, w, L), the ratio of production rules (in Fig.). In this case time is fixed
of the new list last creating per attributes (c, w, L), the ratio of production rules (in Fig.). In this case time is fixed 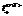 and ratio cardinal number which is constant in case of fulfillment of a condition
and ratio cardinal number which is constant in case of fulfillment of a condition
 , (1)
, (1)
where  – integral error estimation of the system operation
– integral error estimation of the system operation 
 – maximum integral error of the first adjustment period
– maximum integral error of the first adjustment period 
The end of internal paces total time (TdS) is determined using the following formula
 , (2)
, (2)
where a, b – are coefficients of pace movements variation that are introduced to provide additional conditions of optimized structure operational reliability.
In this case the 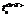 value is interpreted as an approximate time of training completion. The system transfer into classification mode is performed in case of the condition fulfillment
value is interpreted as an approximate time of training completion. The system transfer into classification mode is performed in case of the condition fulfillment
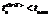 , (3)
, (3)
taking into account the 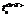 value adjustment at the end of each period of internal pace movement according to
value adjustment at the end of each period of internal pace movement according to 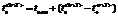 . (4)
. (4)
where tnom is a current time value.
Statistical method of structure optimization of the neuro-fuzzy rules base of intelligent ACS elements. In order to reduce the algorithm running time and improve its efficiency when performing parametric synthesis of asymptotically stable intelligent control systems we propose an expert method determining the concentration coefficient of membership functions and sampling limits for further adjustments to the base of the adaptive-established rules.
Since the exact values of probabilistic characteristics (a priori probability P(Vk) and conditional probability P(Ai/Vk) of finding an object Z in one of the possible classes Vk, with collective expert evaluation of information systems with algorithms Ai) are often unknown, their evaluation is recommended [6] to be carried out with regard to the relevant frequencies
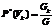 , (5)
, (5)
 , (6)
, (6)
where Gk is the number of k class appearances (k = 1, ..., M) in the sampling out of G observations; Eki is the number of erroneous decisions and i information system (i = 1, ..., N) in the analysis of situations where Z belongs to the k class.
 Erroneous decisions can be determined at a stage when reliable information about the state of the object is obtained. At this stage it is necessary to form the classes in which the system was located at the previous step (in the neural network technologies such control sampling is called the indication of a "teacher"): y[1], y[2], …, y[G], where y[n] Î {1, …, M}.
Erroneous decisions can be determined at a stage when reliable information about the state of the object is obtained. At this stage it is necessary to form the classes in which the system was located at the previous step (in the neural network technologies such control sampling is called the indication of a "teacher"): y[1], y[2], …, y[G], where y[n] Î {1, …, M}.
The value of a priori probability P(Vk) and conditional probability P(Ai/Vk) of finding a Z object in one of the possible Vk classes allows calculating a collective decision on the state for the application environment y[1], y[2], …, y[G], where y[n] Î {1, …, M}. The decision rule for collective decision-making is [6]
 (7)
(7)
The existing value of the collective solution (7) is used as the coordinate of the b maximum of the membership function of the x variable of arbitrary fuzzy terms Т – mT(b) = 1 for Gaussian type phase transitions.
Concentration ratio c of phase transitions is calculated using the following procedure.
Let's denote partial solutions of information systems on the object state using di, i = 1, 2, …, N, where N is a total number of Information Systems that are used to identify the state of the application environment. A set of Information Systems which determined that the object state refers to the m class we denoted as Im, m = 1, 2, …, M.
Since Ii Ç Ij = 0 "i, j = 1, …, M it is necessary to determine the following values:
– a set of information systems (I*) with the solution coincided with the collective decision ( ) on the state in which the application environment is y[1], y[2], …, y[G], where y[n] Î {1, …, M};
) on the state in which the application environment is y[1], y[2], …, y[G], where y[n] Î {1, …, M};
– percentage (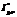 ) of information systems with solutions coincided with the collective one;
) of information systems with solutions coincided with the collective one;
– a set of information systems (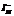 ) and their percentage
) and their percentage  with the solution that did not coincide with the collective decision calculated according to the collective decision rule (7).
with the solution that did not coincide with the collective decision calculated according to the collective decision rule (7).
According to this method the value  characterizes a dynamic state of the object which may be classified as the state that belongs to the term with the coordinate of the b maximum.
characterizes a dynamic state of the object which may be classified as the state that belongs to the term with the coordinate of the b maximum.
In general, the number of possible combinations of partial solutions is MN. In the M case decisions will be consisted. In addition, the concentration factor is adopted at the level of the minimum value Xmax – 0,99 × Xmax, which provides a range of variation of the variable (x) within a reasonable error at a zero a-level of the membership function.
If there are percentage advantages, the concentration ratio of the membership function may be calculated as follows:
 ,(8)
,(8)
where 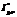 – is the percentage value of information systems with their solutions coincided with the collective one;
– is the percentage value of information systems with their solutions coincided with the collective one;  ,
,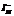 – the percentage value and the set of information systems with their solutions did not coincide with the collective decision calculated according to the collective decision rule (7).
– the percentage value and the set of information systems with their solutions did not coincide with the collective decision calculated according to the collective decision rule (7).
According to the developed technique it is possible to compare the membership function parameters, which have been obtained as a result of the work of the modified adaptive algorithm of the Wang–Mendel fuzzy network and the doubling parameters obtained on the basis of statistical processing of information systems solutions of identification of the dynamic object state (7).
There is an implementation of the adaptive adjustment algorithm of the neuro-fuzzy emulator vector parameters of inverse dynamics of the object with optimization of the membership functions parameters:
а) initial values of the fuzzy controller parameter vector w are copied to the spare array. At first the parameters w are explicitly defined as ACS goes into working condition after performing prior configuration neuro-fuzzy emulator where the operator is copied by a controller;
b) let's calculate the error e(t + 1) and dk according to [4];
c) weights of synaptic connections are determined;
d) the structure and parameters of production rules are corrected according to intercomparison of adaptive-formed values and the result obtained on the basis of collective decision rule (7).
Here is a systems operation algorithm taking into account the developed method of self-organization of neuro-fuzzy structures based on the FOREL class taxonomy algorithm.
1. The first cluster with a center is created at the start of the first data pair. We believe that the power of the set is L1 = 1.
2. After reading the k training pair the FOREL class taxonomy algorithm is applied to determine the conditions for creating a new cluster.
FOREL class taxonomy algorithm [7] is based on a quality criterion of taxonomy F. It is based on the compactness hypothesis: one taxon should include objects that are "similar" in their properties to some "central" object, i.e. objects similar to each other in their characteristics must fall into one taxon. The result is a spherical shape taxon. Let's introduce the following notations: Cj are coordinates of the center of the j taxon (center of the membership function); mj is the number of objects in the j taxon;  are objects of the j taxon; r(Cj, a) is the distance between the center and the i element of the j taxon.
are objects of the j taxon; r(Cj, a) is the distance between the center and the i element of the j taxon.
The sum of distances from all elements to the j taxon center is determined by the formulation:
 , (9)
, (9)
where m – is the number of objects in the set which is to be divided into groups.
The sum of internal distances to all taxons is determined by the formula
 . (10)
. (10)
The essence of the criterion is that one needs to find such a partition of m objects of taxons, so that the above stated value F was minimal. This condition is achieved by using a FOREL algorithm.
The taxons that are defined by this algorithm have a spherical shape. The number of taxons depends on the radius of the spheres: the smaller the radius, the more taxons are there. At first the signs of objects are allocated so that the values of all the signs were in the range from zero to one. Then a hypersphere of the minimum radius R0 is constructed. It covers all the m points (all objects belong to the same taxon). Then the spheres radius gradually decreases. The radius 0,9 R0 is assigned and the center of the sphere is transferred to any of the available points. Then we find points, the distance to which is less than the radius, and calculate the gravity center coordinates of these "internal" points. We transfer the center of the sphere in the new gravity center and find internal points again.
This procedure for determining the internal points and shifting the center of the sphere continues until the sphere stops, that is, until we determine that the composition of internal points and, consequently, their gravity center are not changed. This means that the sphere has stopped within a local maximum of dots' density of the features in space.
The points trapped inside the sphere are declared to belong to the first taxon. They are excluded from further consideration. And the base is refilled with the following values: cM+1(k)=xk; wM+1(k)=yk,; LM+1(k)=1.
Parameters of clusters established before are not changed: wl(k)=wl(k–1); Ll(k)=Ll(k–1) for l=1, …, M.
For remaining points the above mentioned procedure is repeated until all points are included in the taxons.
If a result of the algorithm operation determines that the current coordinates are included in the lk cluster, the cluster parameters are specified according to the classical adjustment algorithm of Wang–Mendel neuro-fuzzy network parameters [5].
3. The output of the system is calculated according to resulting function that approximates the input data [4].
4. In the period of time TdS there is an integral error accumulation of the system operation and dynamic parameter settings of Wang-Mendel neuromorphic structure according to the developed method.
5. System is transferred to perform steps 1–4 granted there is an increase of the control integral error.
The authors has developed an efficient algorithm for neuro-fuzzy self-organizing structures. Self-organization algorithm provides adaptive correction of membership functions parameters with a minimal critical mistake. The proposed synthesis technique can be used in the design of complex intelligent control systems of dynamic objects, as well as serve as a basis for the development of efficient algorithms for intelligent control.
References
1. Uskov A., Kruglov V. Intellektualnye sistemy upravleniya na osnove metodov nechetkoy logiki [Intelligent Control Systems Based on Fuzzy Logic Methods]. Smolensk, 2003.
2. Verbruggen H.B., Babuska R. Constructing fuzzy models by product space clustering. Fuzzy model identification. H. Hellendorn, D. Driankov (Eds.). Berlin, Springer, 1998, pp. 53–90.
3. Kruglov V., Borisov V. Iskusstvennye neyronnye seti. Teoriya i praktika [Artificial Neural Networks. Theory and Practice]. Мoscow, Goryachaya Liniya–Telekom Publ., 2001.
4. Development of a methodology of synthesis and statement of reasons for the implementation of intelligent hybrid technologic processes automatic control systems based on neural network structures and methods of fuzzy logic. Report of the R&D, Krivoy Rog Technical Univ. Publ., Krivoy Rog, 2006, 250 p. (in Ukr.).
5. Osowski S. Neural networks for information processing. Warsaw, Oficyna Wydawnicza Politechniki Warszawskiej Publ., 2000, 304 p. (Russ. ed.: Rudinskiy I.D. Moscow, Finansy i Statistika Publ., 2002, 345 p.).
6. Fainsilberg L. Taught support system of collective decision of the independent experts group. Upravlyayushchie sistemy i mashiny [Control Systems and Machines]. 2003, no. 4, pp. 62–67.
7. Zagoruyko N. Prikladnye metody analiza dannykh i znany [Applied Approaches to Data Analysis and Knowledge]. Novosibirsk, Institute of Mathematics Publ. House, 1999, 261 p.
Литература
1. Усков А.А., Круглов В.В. Интеллектуальные системы управления на основе методов нечеткой логики. Смоленск,
2003.
2. Verbruggen H.B., Babuska R. Constructing fuzzy models by product space clustering. Fuzzy model identification. Eds.
H. Hellendorn, D. Driankov. Berlin, Springer, 1998, pp. 53–90.
3. Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. М.: Горячая линия–Телеком, 2001.
4. Розроблення методології синтезу та обґрунтування доцільності впровадження інтелектуальних гібридних систем
автоматичного управління технологічними процесами на основі нейромережевих структур та методів нечіткої логіки: Звіт з
НДДКР № ДР0104U004720. Кривий Ріг: Криворізький техн. університет. 2006. 250 с.
5. Осовский С. Нейронные сети для обработки информации; [пер. с польск.]. М.: Финансы и статистика, 2002, 345 с.
6. Файнзильберг Л.С. Обучаемая система поддержки коллективного решения группы независимых экспертов
// Управляющие системы и машины. 2003. № 4. С. 62–67.
7. Загоруйко Н.Г. Прикладные методы анализа данных и знаний. Н.: Изд-во Ин-та математики, 1999. 261 с.
 is a variable value which is formed by the system based on time analysis
is a variable value which is formed by the system based on time analysis 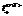 of the new list last creating per attributes (c, w, L), the ratio of production rules (in Fig.). In this case time is fixed
of the new list last creating per attributes (c, w, L), the ratio of production rules (in Fig.). In this case time is fixed  , (1)
, (1) – integral error estimation of the system operation
– integral error estimation of the system operation 
 – maximum integral error of the first adjustment period
– maximum integral error of the first adjustment period 
 , (2)
, (2)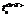 value is interpreted as an approximate time of training completion. The system transfer into classification mode is performed in case of the condition fulfillment
value is interpreted as an approximate time of training completion. The system transfer into classification mode is performed in case of the condition fulfillment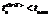 , (3)
, (3)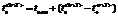 . (4)
. (4)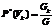 , (5)
, (5) , (6)
, (6)
 (7)
(7) ) on the state in which the application environment is y[1], y[2], …, y[G], where y[n] Î {1, …, M};
) on the state in which the application environment is y[1], y[2], …, y[G], where y[n] Î {1, …, M};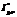 ) of information systems with solutions coincided with the collective one;
) of information systems with solutions coincided with the collective one;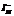 ) and their percentage
) and their percentage  with the solution that did not coincide with the collective decision calculated according to the collective decision rule (7).
with the solution that did not coincide with the collective decision calculated according to the collective decision rule (7). ,(8)
,(8) are objects of the j taxon; r(Cj, a) is the distance between the center and the i element of the j taxon.
are objects of the j taxon; r(Cj, a) is the distance between the center and the i element of the j taxon. , (9)
, (9) . (10)
. (10)