Journal influence
Bookmark
Next issue
Abstract:
Аннотация:
| Authors: Eremeev, A.P. (eremeev@appmat.ru) - National Research University “MPEI” (Professor), Moscow, Russia, Ph.D, () - | |
| Keywords: representation of knowledge, , artificial intelligence, fuzzy logic, CAD system |
|
| Page views: 19630 |
Print version Full issue in PDF (8.40Mb) |
Потребность в мощных интеллектуальных средствах поддержки принятия решений, равно как и а также в инструментахсредствах прямого интеллектуального управления технологическими объектами крайне высока. Она обусловлена растущим уровнем автоматизации и скоростью протекания контролируемых и управляемых процессов, их увеличивающейсявозрастающей сложностью и высоким уровнем ответственности за принимаемые решения. Отсюда следуют такие требования к интеллектуальным системам, основанным на знаниях, как их верифицируемость и быстродействие. При том известноИзвестно, что выразительность и гибкость моделей представления знаний находятся, как правило, в обратной зависимости от их эффективности. Чем больше опций и вариантов использования предлагает модель, чем богаче ее язык, тем сложнее ее обработка [1]. Целесообразна разработка полного инструментария для работы с достаточно выразительными табличными моделями представления знаний с учетом широких возможностей их верификации и оптимизации, а также эффективного принятия решений на основе таких моделей. Предлагается расширить классический аппарат таблиц решений (ТР) [2,3], вводя в него нечеткость и применяя методы теории приближенных множеств. ПредлагаетсяОпишем обобщенную формальную модель для такого класса табличных моделей, алгоритм принятияпоиска решений по ним, основывающийся на схеме вывода Цукамото для нечетких правил, а также способ повышения эффективности вывода с применени- ем деревьев активации. На основании предлагаемых моделей разрабатываются инструментальные средства, обеспечивающие поддержку полного жизненного цикла табличных моделей, включая их изначальное задание и редактирование, верификацию и оптимизацию таблиц, а также принятие решений по ним в автоматическом и полуавтоматическом режимах. Работы по данному проекту выполняются в контекстеплане НИР кафедры ПМприкладной математики МЭИ (ТУ) и в сотрудничестве с Техническим университетом г. Дрездена (Германия). Нечеткие ТР Классические ТР известны с конца 60-х годов XX века. В 1979 году был принят Европейский стандарт DIN 66241 «Обработка информации. Таблицы решений в качестве описательных средств в процессе принятия решений», но тем не менееоднако в различных работах можно найти отличающиеся описания структуры ТР и их семантики. В своей базовой форме язык ТР позволяет задавать набор простых продукционных правил Множества входных термов (условий) Построим формальное описание нечетких ТР (НТР), базирующихся на классических ТР, но способных работать как с дискретными, так и с непрерывными и нечеткими входами и выходами. Идея такой гибридизации появилась в литературе в середине 90-х годов XX века, однако в имевшихся публикациях не была четко сформулирована формальная модель НТР, нечеткие входы таблиц рассматривались в отрыве от стандартных дискретных, что не позволяет говорить об эффективном обобщении аппарата ТР на нечеткий случай [4]. Для вывода по НТР использовались стандартные общие схемы нечетких рассуждений, не использующие особенности НТР для построения более эффективных специализированных алгоритмов вывода. Определим атрибут как тройку: В рамках этой общей структуры выделим несколько базовых классов атрибутов: булевы атрибуты, N-значные дискретные, вещественные и нечеткие атрибуты. Эти подклассы получаются из общего определения атрибута наложением ограничений на его компоненты. Например, подкласс нечетких атрибутов определим как атрибуты вида В дальнейшем, говоря об определенном атрибуте Введем дополнительные понятия: · входной вектор (ситуация), принадлежащий множеству возможных ситуаций · выходной вектор (решение), принадлежащий множеству решений Тогда процесс принятия решений можно представить как отображение входных ситуаций на решения посредством НТР: Знания в виде функции F могут быть представлены и как набор продукционных правил специального вида. Пусть даны В антецеденте и консеквенте правила записываются нечеткие конъюнкции оценок значений атрибутов НТР, а само правило является не достоверным, а правдоподобным с коэффициентом уверенности Как и в классических ТР, такие правила могут быть представлены в табличном виде, где решающие правила записываются в столбцах, а строки таблицы соответствуют условным и решающим атрибутам НТР. Во входах условной части НТР применяется символ безразличия «*», если значение условного атрибута несущественно в правиле. В последней строке таблицы записываются коэффициенты уверенности правил. Отметим, что классические ТР являются частным случаем НТР, где используются только булевы атрибуты, а коэффициенты уверенности всех правил полагаются равными 1,0. Для принятия решений по описанной структуре НТР предложен алгоритм вывода, основывающийся на известных схемах вывода для нечетких баз правил. В алгоритме единообразно обрабатываются все классы атрибутов. Также предложена концепция дерева активации, позволяющего ускорить процесс отбора активных правил и сделать процесс вывода более эффективным. В данной статье детали процесса вывода подробно не рассматриваются. Структура мультитабличной модели Одиночная ТР позволяет задавать логику принятия решения в некотором классе ситуаций, характеризуемых набором условных атрибутов таблицы. Для построения моделей, способных функционировать в достаточно широком классе ситуаций, целесообразно перейти от однотабличной к мультитабличной модели и задать логику принятия решений не в виде единственной НТР, а через набор связанных таблиц. Это позволяет уменьшить размеры отдельных таблиц и обрабатывать их независимо друг от друга. В то же время, если таблицы в модели содержат знания о функционировании одной проблемной области (но, например, в различных режимах), некоторые условные атрибуты будут входить в несколько НТР. Таким образом, во избежание дублирования и рассогласования описаний следует хранить определения атрибутов не в заголовках НТР, а централизованно, в репозитории атрибутов мультитабличной модели. В заголовках НТР тогда достаточно помещать лишь ссылки на уникальные идентификаторы атрибутов.
Рис. 1. Визуализация XSD-схемы хранения мультитабличной модели Определим мультитабличную модель представления знаний как набор Сам процесс принятия решений по мультитабличной модели может быть одно- и многошаговым. Под шагом принятия решения подразумевается вывод на одной активной НТР с получением значений выходных атрибутов и, возможно, новой активной НТР. В случае одношагового принятия решений процесс на этом завершается, в то время как многошаговое принятие решений подразумевает непосредственное продолжение вывода на новой активной НТР. Процесс вывода при многошаговом сценарии может быть организован и как потенциально бесконечный циклический опрос условий-датчиков с выдачей управляющих значений аналогично принципу работы промышленного контроллера. Для явного прерывания процесса область значения атрибута NextTable расширяется символом STOP. Экземпляры мультитабличной модели могут быть сериализованы в XML-представление, описываемое XSD-схемой, визуализация которой, построенная в редакторе XMLSpy, приведена на рисунке 1. В схеме объявлено пространство имен по умолчанию (http://www.appmat.ru/decider); корневым тегом является DecisionModel. В соответствии со структурой мультитабличной модели в него вложены теги представления репозитория атрибутов (Repository) и отдельных НТР (DecisionTables), а также некоторые служебные данные. В частности, с моделью в целом (и с отдельными атрибутами, значениями атрибутов и НТР) связан тег метаданных типа MetaDataType, включающий имя и содержательное описание соответствующего элемента данных. Особенностью предлагаемой схемы является расширяемость, позволяющая доопределять ее и повторно использовать для обмена мультитабличными моделями между различными реализациями программных компонентов, использующих, помимо базовой структуры модели, различные ее уточнения. Расширяемость достигается за счет ассоциирования с тегами атрибутов (Attribute), НТР (DecisionTable) и отдельных решающих правил (Rule, ElseRule) абстрактных элементов расширения ExtraData, допускающих многократное повторение. При необходимости введения в модель дополнительных данных нужно определить в расширенной схеме новый тип элемента, наследующий от одного из абстрактных типов AttributeExtraDataType, TableExtraDataType или RuleExtraDataType соответственно. В базовой схеме через такие элементы расширения задаются сложности проверки условий, отношение линейного порядка на множестве значений атрибута, диапазоны допустимых входных значений и границы областей разбиения домена для вещественных и нечетких атрибутов, тип функции принадлежности нечетких атрибутов, коэффициенты активации правил в НТР, частоты применимости правил и др.
Рис. 2. Диаграмма взаимосвязей компонентов системы При сериализации дополнительных данных в XML-формате необходимо указывать настоящий (доопределенный) тип элемента ExtraData посредством системного атрибута type из пространства имен (http://www.w3.org/2001/XMLSchema-instance). Например, определив в схеме неабстрактный тип тега RealAttributeExtraData, предназначенный для сохранения определения домена вещественного атрибута и наследующий от абстрактного типа AttributeExtraDataType, можно использовать его в XML-представлении мультитабличной модели, вложив в соответствующий тег Attribute: <ExtraData xmlns:xsi="http://www.w3.org/2001/XMLSchemainstance" xsi:type="RealAttributeExtraData"> <DomainLimits domMax="40.0" domMin="0.0"/> <Thresholds> <Threshold>10.0</Threshold> <Threshold>30.0</Threshold> </Thresholds> </ExtraData> Архитектура программной системы На основе изложенного формального аппарата была реализована программная система модульного типа. Разработка велась на языке С++ в средах Microsoft Visual Studio 2005 и Borland Developer Studio 2006 с ориентацией на IBM-совместимые ЭВМ с ОС Microsoft Windows 98/ME/2000/XP. На рисунке 2 приведена диаграмма взаимосвязей компонентов системы. Динамические библиотеки Support, xerces-c и TestFramework являются вспомогательными. Модуль xerces-c представляет собой C++-версию библиотеки обработки XML-документов Xerces с открытым исходным кодом, изначально разработанную в рамках проекта Apache. Библиотека TestFramework содержит базовые классы и макросы поддержки модульного тестирования, построенные на базе известного открытого каркаса тестирования CppUnitLite. В библиотеку Support входят служебные классы и функции общего назначения. Основные операции сохранения/загрузки, представления и обработки мультитабличных моделей и принятия решений по ним реализованы в библиотеке Decider. Библиотеки RSMain и Dependency содержат реализации методов базовой теории приближенных множеств и ее нечеткого обобщения [6]. Корректность реализации кода в библиотеках Decider, Cardinals, Dependency, RSMain подтверждена множественными модульными тестами в исполняемых сборках DeciderUnitTests.exe и RoughUnitTests.exe с общим количеством выполняемых проверок, превышающим 1000 проверяемых условий в каждой из сборок. Для визуализации результатов модульного тестирования используется свободно распространяемая утилита Unit Test’s Reporter (см. http://www.codeproject.com/ KB/cpp/UnitTestsReporter.aspx). Все перечисленные библиотеки используются исполняемым модулем SIMPR (рис. 2), который реализует систему моделирования принятия решений СИМПР-Windows [6]. Данная система является развитием разработок в области табличных моделей принятия решений, ведущихся на кафедре прикладной математики Московского энергетического института. Первые версии системы поддерживали только классические ТР с ограниченным (бинарным) входом, более поздние версии расширены методами анализа и оптимизации ТР более общей структуры. Объектное представление мультитабличной модели, соответствующее архитектуре разработанного ПО, приведено в виде диаграммы классов на рисунке 3. Диаграммы классов построены в CASE-средстве Rational Rose EE 2002 с использованием языкового расширения ANSI C++. Иерархия классов, моделирующих атрибуты, включает корневой абстрактный класс CAttribute и его наследников CBinaryAttribute, CNValuedAttribute, CRealAttribute, CFuzzyAttribute, представляющих булевы, дискретные, вещественные и нечеткие атрибуты соответственно.
Рис. 3. Диаграмма классов компонентов мультитабличной модели
Рис. 4. Диаграмма классов представления входных/выходных ситуаций
Рис. 5. Диаграмма классов решателей
Рис. 6. Сценарий жизненного цикла мультитабличной модели Кроме представления структуры мультитабличной модели, объектная модель должна также иметь классы для представления входных и выходных ситуаций. На рисунке 4 представлена иерархия классов ситуаций, начиная от абстрактного интерфейса ISituation. Предлагаемые классы реализуют как непосредственное хранение элементов ситуации в массиве (CVectorSituation), так и делегирование запросов к внешним функциям (CDynamicSituation) либо иным реализациям интерфейса ISituation с возможностью кэширования получаемых результатов (CBaseProxySituation). Наличие у класса CBaseProxySituation двух потомков объясняется ограничением в них прав доступа к представлению-делегату только на чтение (CROProxySituation) либо на чтение и обновление (CProxySituation) компонентов ситуации. Для принятия решений по НТР реализованы два решателя: CNaiveFuzzyDecider и CATFuzzyDecider (рис. 5). Особенностью последнего является использование дерева активации (CActivationTree) для ускорения отбора активных правил в НТР. Оба решателя реализуют один программный интерфейс IFuzzyDecider, поэтому являются взаимозаменяемыми для клиентского кода. Методика применения мультитабличных моделей Описанная архитектура программной системы предполагает методику использования табличных моделей представления знаний, схематично показанную на рисунке 6. При участии эксперта и инженера по знаниям производится первоначальная концептуализация проблемной области, результатом которой должен стать репозиторий условных и решающих атрибутов. На основе выделенных атрибутов формируются одна или несколько взаимосвязанных НТР (мультитабличная модель принятия решений). Этот этап выполняется в графической среде СИМПР-Windows, и при многосеансовой работе с мультитабличной моделью она может сохраняться в виде XML-файла описанной выше структуры. Построенные таблицы на втором этапе подвергаются анализу на противоречивость и полноту (при необходимости), затем производится их оптимизация на основе методов теории приближенных множеств. В среде СИМПР-Windows реализованы несколько алгоритмов оптимизации и анализа, включая переборные и матричные алгоритмы, алгоритмы на основе метода кардинальных чисел и нечеткого обобщения теории приближенных множеств. Если в ходе анализа выявляется неполнота либо противоречивость модели, производятся возврат на предыдущий этап и устранение некорректности. Сформированная модель на третьем этапе транслируется в бинарное хранимое представление для повышения эффективности последующего поиска решений. В ходе трансляции для каждой НТР может строиться связанное с ней дерево активации с учетом одного из возможных критериев оптимальности. Оттранслированная модель может применяться для непосредственного принятия решений в проблемной области. Для этого она должна быть загружена в компонент интерпретатора, активированный для принятия решения по некоторой заданной входной ситуации. Возможны 3 варианта использования. В первом случае (этап 4 на рис. 6) используется экземпляр интерпретатора, встроенный непосредственно в среду СИМПР-Windows. Этот сценарий применяется для тестирования модели на адекватность. В случае обнаружения недопустимого поведения требуются коррекция модели и ее последующий повторный анализ и ретрансляция (то есть возврат на этап 1). По завершении тестирования табличная модель используется без привлечения среды СИМПР (этапы 5 и 6). В случае небольшой проблемной области и отсутствия специфических требований к интерфейсу ввода/ввода данных (либо в ходе прототипирования системы) может быть автоматически построена мини-ЭС, консультирующая ЛПР посредством диалоговых окон ввода данных ситуации и вывода рекомендуемых действий на основе стандартных элементов пользовательского интерфейса ОС Windows (этап 5). В более сложных ситуациях рекомендуется встраивание программного компонента интерпретации НТР в специфическую среду принятия решений (этап 6). При этом в вызывающей системе становится возможным не только реализация поддержки принятия решений по мультитабличной модели путем диалога системы с ЛПР, но и полностью автоматическое принятие решений с их выдачей по программным интерфейсам на исполняющие устройства либо другие программные компоненты. Полученные результаты и реализованная на их основе программная система применялись для решения задачи диспетчеризации лотов на производстве микроэлектронных компонент. Совместно с Дрезденским техническим университетом разрабатывается программный комплекс, позволяющий в реальном времени управлять стратегиями диспетчеризации производимых лотов микроэлектронных чипов между обрабатывающими устройствами в цехе с функциональной группировкой оборудования. Предложенные подходы и программные средства используются также для создания перспективных интеллектуальных систем поддержки принятия решений реального времени для мониторинга и управления сложными техническими объектами и процессами на примере объектов энергетики. Список литературы 1. Вагин В.Н., Еремеев А.П. Некоторые базовые принципы построения интеллектуальных систем поддержки принятия решений реального времени. // Изв. РАН. Теория и система управления, 2001. – № 6. – С. 114–123. 2. Еремеев А.П. Продукционная модель представления знаний на базе языка таблиц решений. // Изв. АН СССР. Техническая кибернетика, 1987. – № 2. – С. 196–209. 3. Еремеев А.П. О корректности продукционной модели принятия решений на основе таблиц решений. // Автоматика и телемеханика. – 2001. – № 10. – С. 78–90. 4. Chen G., Vanthienen J., Wets G. Fuzzy decision tables: extending the classical formalism to enhance intelligent decision making. // Proc. of the Fourth IEEE International Conf. on Fuzzy Systems, 1995, vol. 2, pp. 599–606. 5. Леоненков А.В. Нечеткое моделирование в среде MATHLAB и fuzzyTECH. – СПб: БХВ-Петербург, 2003. 6. Виноградов О.В., Еремеев А.П. Использование таблиц решений с расширенным входом в интеллектуальных системах поддержки принятия решений. // Тр. 10-й Нац. конф. по искусствен. интеллекту с междунар. участ.: КИИ-2006: – М.: Физматлит, 2006. – Т. 3. – С. 807–815.
|
| Permanent link: http://swsys.ru/index.php?id=1622&lang=en&page=article |
Print version Full issue in PDF (8.40Mb) |
| The article was published in issue no. № 4, 2008 |
Perhaps, you might be interested in the following articles of similar topics:
- Программная реализация адаптивной компонентной автоматизированной обучающей системы
- Интеграция методов обучения с подкреплением и нечеткой логики для интеллектуальных систем реального времени
- Задачи построения интеллектуальной информационной системы управления безопасностью дорожного движения
- Структурная схема нечеткого регулятора на основе лингвистических переменных с четкими термами
- Реализация методов обучения с подкреплением на основе темпоральных различий и мультиагентного подхода для интеллектуальных систем реального времени
Back to the list of articles
 на основе пропозициональной логики:
на основе пропозициональной логики: 
 .
. и выходных термов (действий)
и выходных термов (действий)  являются общими для всех правил в ТР. Такой набор правил может быть представлен в табличной форме, что и дало название данному формальному аппарату.
являются общими для всех правил в ТР. Такой набор правил может быть представлен в табличной форме, что и дало название данному формальному аппарату.
 , где
, где  – множество входных значений (домен) атрибута
– множество входных значений (домен) атрибута 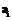 ;
;  – конечное множество выходных значений атрибута
– конечное множество выходных значений атрибута  ;
;  – тотальная функция соответствия значений атрибута
– тотальная функция соответствия значений атрибута  выходного значения
выходного значения  элементу домена
элементу домена  ;
;  – множество всех атрибутов указанной структуры.
– множество всех атрибутов указанной структуры.
 , где
, где 

 ;
;  , где
, где 

 – стандартное определение нечеткой переменной с именем
– стандартное определение нечеткой переменной с именем  , характеризуемой нечетким множеством
, характеризуемой нечетким множеством  с функцией принадлежности
с функцией принадлежности  ;
; 
 [5].
[5]. , будем обращаться к его компонентам также в функциональном стиле, то есть
, будем обращаться к его компонентам также в функциональном стиле, то есть  ,
,  . Определим НТР как тройку
. Определим НТР как тройку 
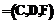 , где
, где  – конечное множество условных атрибутов (условий);
– конечное множество условных атрибутов (условий);  – конечное множество решающих атрибутов (решений, действий);
– конечное множество решающих атрибутов (решений, действий);  – обобщенная решающая функция (функция уверенности).
– обобщенная решающая функция (функция уверенности).
 , – вектор
, – вектор  ;
;
 , – вектор
, – вектор  .
.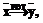
 .
. ,
,  ,
,  и известно, что
и известно, что  . Последнее равенство интерпретируется как решающее правило вида: IF
. Последнее равенство интерпретируется как решающее правило вида: IF  THEN
THEN  с коэффициентом уверенности cf.
с коэффициентом уверенности cf. , равным значению функции уверенности F от значений атрибутов. При
, равным значению функции уверенности F от значений атрибутов. При  правило является достоверным.
правило является достоверным.
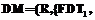
 , где
, где  является репозиторием атрибутов, а
является репозиторием атрибутов, а  – НТР, определение которой модифицировано, так как множества
– НТР, определение которой модифицировано, так как множества  и
и  состоят из ссылок на атрибуты из множества R. НТР в составе одной мультитабличной модели взаимосвязаны. Эти взаимосвязи проявляются в том, что одна НТР может активизировать другую при определенных условиях, но только одна НТР в процессе принятия решения в каждый момент является активной. С каждым правилом в НТР свяжем системный многозначный атрибут NextTable, областью значений которого являются порядковые индексы НТР в составе модели. При принятии решения по этой НТР на основе активированных правил будет выведено выходное значение для атрибута NextTable, указывающее на смену активной НТР для очередного цикла принятия решений. Заметим, что по умолчанию текущая НТР сохраняет свою активность на следующем цикле, так что часть входов в таблице для атрибута NextTable явно может быть не задана. Таким образом, в рамках НТР описываются как непосредственно логика принятия решений, так и метазнания о смене модели поведения при наступлении определенных условий.
состоят из ссылок на атрибуты из множества R. НТР в составе одной мультитабличной модели взаимосвязаны. Эти взаимосвязи проявляются в том, что одна НТР может активизировать другую при определенных условиях, но только одна НТР в процессе принятия решения в каждый момент является активной. С каждым правилом в НТР свяжем системный многозначный атрибут NextTable, областью значений которого являются порядковые индексы НТР в составе модели. При принятии решения по этой НТР на основе активированных правил будет выведено выходное значение для атрибута NextTable, указывающее на смену активной НТР для очередного цикла принятия решений. Заметим, что по умолчанию текущая НТР сохраняет свою активность на следующем цикле, так что часть входов в таблице для атрибута NextTable явно может быть не задана. Таким образом, в рамках НТР описываются как непосредственно логика принятия решений, так и метазнания о смене модели поведения при наступлении определенных условий.




