Искусственные нейронные сети являются эффективным инструментом при решении ряда прикладных задач. Несмотря на это, широкое распространение метод получил относительно недавно, в основном благодаря интенсивному развитию вычислительной техники, позволяющей получить решение задачи в приемлемые сроки. Круг решаемых искусственными нейронными сетями задач постоянно расширяется, в результате повышается актуальность работ в данном направлении.
Часто при решении конкретной прикладной задачи методом искусственных нейронных сетей возникает потребность в моделировании сети нетривиальной топологии. Стандартные методы обучения нейронных сетей могут оказаться в данной ситуации неприменимыми, и поэтому необходимо сформулировать и реализовать индивидуальный алгоритм.
В данной работе рассматривается сеть, динамика которой описывается нелинейной системой рекуррентных уравнений с запаздыванием, задача ее обучения формулируется как дискретная задача оптимального управления.
Цель статьи – описание построения и реализации алгоритма обучения сети указанной топологии.
Динамика работы рассматриваемой нейронной сети описывается следующей системой рекуррентных соотношений:
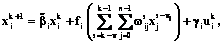 (1)
(1)
k=0, …, q–1, i=1, …, n,
где 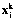 – состояние нейрона i в слое k;
– состояние нейрона i в слое k; 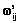 – весовой коэффициент, связывающий нейрон i слоя s с нейроном j слоя s–1;
– весовой коэффициент, связывающий нейрон i слоя s с нейроном j слоя s–1;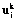 – внешнее воздействие на нейрон i слоя k;
– внешнее воздействие на нейрон i слоя k; 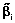 – коэффициент затухания для нейрона i (одинаков для всех слоев); gi – коэффициент передачи внешнего управления на нейрон i; v, vi – глобальная и индивидуальная задержки в передаче сигналов.
– коэффициент затухания для нейрона i (одинаков для всех слоев); gi – коэффициент передачи внешнего управления на нейрон i; v, vi – глобальная и индивидуальная задержки в передаче сигналов.
Заданы начальные условия:
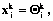 k= –v–max(vi), …, 0, i=1, …, n. (2)
k= –v–max(vi), …, 0, i=1, …, n. (2)
На управление наложены ограничения:
 , (3)
, (3)
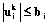 , (4)
, (4)
где aij, bi – заданные положительные параметры модели.
Дискретная задача оптимального управления состоит в построении оптимальных значений весовых коэффициентов, минимизирующих следующую функцию:
 , (5)
, (5)
где 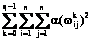 – энергия искусственной нейронной сети;
– энергия искусственной нейронной сети; 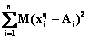 – характеристика состояния системы в конечный момент.
– характеристика состояния системы в конечный момент.
Функция Лагранжа для данной задачи может быть представлена в следующем виде:
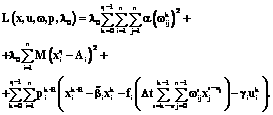 (6)
(6)
Вычислим градиент минимизируемой функции по управлению:
 (7)
(7)
m=0, …, q–1, l=1, …, n, p=1, …, n,
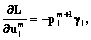 m=0, …, q–1, l=1, …, n, (8)
m=0, …, q–1, l=1, …, n, (8)
где сопряженные векторы удовлетворяют соотношениям
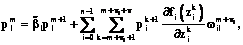 (9)
(9)
m=0, …, q–1, l=1, …, n,
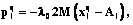 l=1, …, n. (10)
l=1, …, n. (10)
Задача решается методом проекции градиента.
Алгоритм решения сформулированной задачи средствами аппарата математической теории оптимального управления будет следующим.
1. Инициализируем номер итерации: l:=0. Задаем начальное значение шага градиентного спуска s, точность e.
2.  Задаем произвольный набор матриц
Задаем произвольный набор матриц 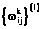 , на диагоналях которых стоят нулевые элементы,
, на диагоналях которых стоят нулевые элементы,  . Кроме того, зададим произвольный набор векторов
. Кроме того, зададим произвольный набор векторов 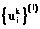 ,
, 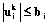 .
.
3. С использованием начальных значений 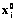 и текущих
и текущих 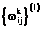 и
и 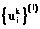 вычисляются
вычисляются 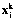 , i=1, …, n, k=1, …, q. В результате получим набор векторов x1, …, xq, который обозначим x(l).
, i=1, …, n, k=1, …, q. В результате получим набор векторов x1, …, xq, который обозначим x(l).
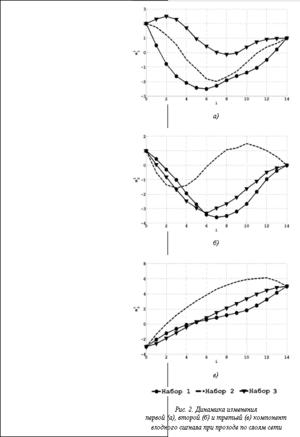
4. Вычисляем значение минимизируемого функционала, используя текущие значения x(l), 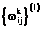 и
и 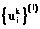 . Обозначим его I(l).
. Обозначим его I(l).
5. Вычисляем сопряженные векторы p(l).
6. Определяем новые весовые коэффициенты и величины внешних воздействий по формулам
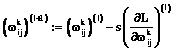 ,
,
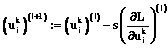 .
.
Если 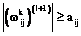 ,
,
то 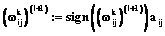 ,
,
если 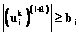 ,
,
то 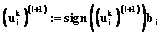 .
.
7. Для полученных значений весовых коэффициентов и значений внешнего воздействия вычисляем значения векторов x(l+1), а затем значение минимизируемого функционала, которое обозначим I(l+1). Вычисляем значение 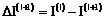 .
.
8. Если  , присваиваем s:=0,5s и переходим к шагу 6.
, присваиваем s:=0,5s и переходим к шагу 6.
9. Если 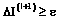 , увеличиваем счетчик итераций l:=l+1 и переходим к шагу 5. В противном случае удовлетворяющая требуемым условиям траектория найдена.
, увеличиваем счетчик итераций l:=l+1 и переходим к шагу 5. В противном случае удовлетворяющая требуемым условиям траектория найдена.
Полученный алгоритм был реализован в программной среде Borland Delphi 7. Анализ результатов работы программы проводился при следующих входных данных: n=3, q=15, s=0,1, e=0,000001, IterMAX=10000, v=2, vi=2, bi=0,1, aij=1, bi=0,5, gi=0,5, M=10, a=0,1, di=1.
Входной вектор: (2 1 –3).
Целевой вектор: (1 0 5).
Начальные условия: Qk1=2, Qk2=1, Qk3= –3, k= –4, …, 0.
На рисунке 1 изображен график зависимости значения минимизируемой функции от номера итерации работы алгоритма для трех различных начальных наборов 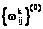 и
и 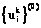 .
.
 На рисунке 2 изображены траектории, отражающие динамику изменения входного сигнала при проходе по слоям сети на последней итерации работы алгоритма. Графики показывают, что выходной вектор нейронной сети стремится к целевому. Метод завершает свою работу по достижении требуемой точности. Однако видно, что траектории приближенного оптимального решения поставленной задачи значительно отличаются друг от друга для различных начальных точек.
На рисунке 2 изображены траектории, отражающие динамику изменения входного сигнала при проходе по слоям сети на последней итерации работы алгоритма. Графики показывают, что выходной вектор нейронной сети стремится к целевому. Метод завершает свою работу по достижении требуемой точности. Однако видно, что траектории приближенного оптимального решения поставленной задачи значительно отличаются друг от друга для различных начальных точек.
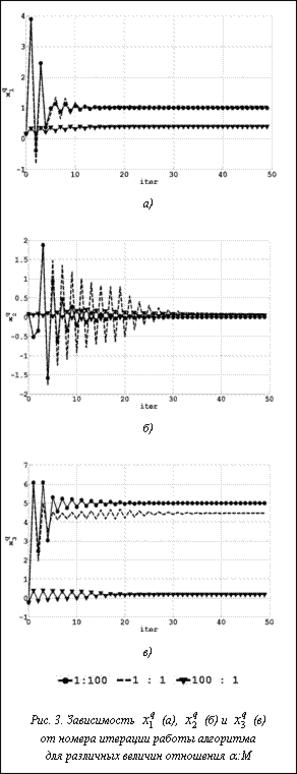
В одних прикладных задачах более приоритетным оказывается минимизирование энергии нейронной сети, в других – как можно более точное попадание в целевую точку. Для управления процессом обучения в пользу минимизации интегрального либо терминального слагаемого в задачу введены штрафные коэффициенты a и M. На рисунке 3 изображены графики зависимости значений отдельных компонент выходного вектора от номера итерации работы алгоритма при различных отношениях величин штрафов интегрального и терминального слагаемых.
При увеличении штрафа терминального слагаемого точность попадания в целевую точку увеличивается, при этом растет энергия сети. Относительное увеличение штрафа интегрального слагаемого ведет к обратному эффекту.
Стоит отметить, что на результат работы алгоритма в значительной степени влияет вид активационной функции. Использование линейной функции активации f(x)=kx приводит к повы- шению точности попадания в целевую точку. Использование же функции активации f(x)= =k×arctg(x) при снижении точности попадания в целевую точку уменьшает время работы алгорит- ма при одних и тех же параметрах задачи и метода.
Предложенная модель является дискретным аналогом нейронной сети, описываемой системой интегро-дифференциальных уравнений с запаздывающим аргументом. Она может использоваться при моделировании управляемых процессов, в которых информационный сигнал, воздействующий на систему в данный момент, накапливается на некотором предшествующем интервале времени.
Литература
1. Применение функционального анализа в теории приближений: Сб. науч. тр. Тверь, Изд-во ТвГУ. 2000.
2. Андреева Е.А., Цирулева В.М. Вариационное исчисление и методы оптимизации. М.: Высш. школа, 2006.
3. Андреева Е.А. Оптимальное управление динамическими системами. Тверь, Изд-во ТвГУ. 1999.
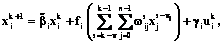 (1)
(1)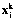 – состояние нейрона i в слое k;
– состояние нейрона i в слое k; 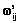 – весовой коэффициент, связывающий нейрон i слоя s с нейроном j слоя s–1;
– весовой коэффициент, связывающий нейрон i слоя s с нейроном j слоя s–1;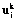 – внешнее воздействие на нейрон i слоя k;
– внешнее воздействие на нейрон i слоя k; 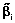 – коэффициент затухания для нейрона i (одинаков для всех слоев); gi – коэффициент передачи внешнего управления на нейрон i; v, vi – глобальная и индивидуальная задержки в передаче сигналов.
– коэффициент затухания для нейрона i (одинаков для всех слоев); gi – коэффициент передачи внешнего управления на нейрон i; v, vi – глобальная и индивидуальная задержки в передаче сигналов.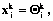 k= –v–max(vi), …, 0, i=1, …, n. (2)
k= –v–max(vi), …, 0, i=1, …, n. (2) , (3)
, (3)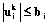 , (4)
, (4) , (5)
, (5)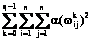 – энергия искусственной нейронной сети;
– энергия искусственной нейронной сети; 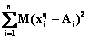 – характеристика состояния системы в конечный момент.
– характеристика состояния системы в конечный момент.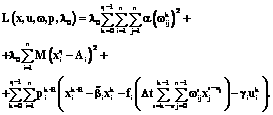 (6)
(6) (7)
(7)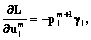 m=0, …, q–1, l=1, …, n, (8)
m=0, …, q–1, l=1, …, n, (8)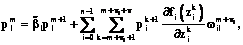 (9)
(9)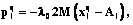 l=1, …, n. (10)
l=1, …, n. (10)
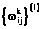 , на диагоналях которых стоят нулевые элементы,
, на диагоналях которых стоят нулевые элементы, 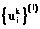 ,
, 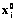 и текущих
и текущих 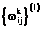 и
и 
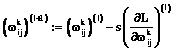 ,
,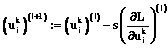 .
.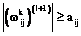 ,
,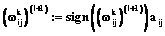 ,
,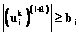 ,
,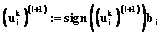 .
.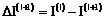 .
. , присваиваем s:=0,5s и переходим к шагу 6.
, присваиваем s:=0,5s и переходим к шагу 6.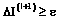 , увеличиваем счетчик итераций l:=l+1 и переходим к шагу 5. В противном случае удовлетворяющая требуемым условиям траектория найдена.
, увеличиваем счетчик итераций l:=l+1 и переходим к шагу 5. В противном случае удовлетворяющая требуемым условиям траектория найдена.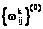 и
и 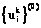 .
.
