Графы широко используются для представления структуры различных систем. В работах [1, 2] описаны матричное и аналитическое представле- ние простых, мульти- и гиперграфов и операции над ними (добавление, удаление вершин и ребер, стягивание и др.), а в [3] приведен подробный анализ использования различных графов для моделирования структуры технических объектов.
Результаты, описанные в указанных работах, не зависят от ПО, которое может использоваться для практического применения в автоматизированных информационных системах (АИС).
Программная среда реализации АИС, в свою очередь, определяет предпочтения на формальное представление графов. Так, в [4] рассматривается применение N-ориентированных гиперграфов и реляционных БД для структурного и параметрического синтеза технических систем. Применение сложных N-ориентированных гиперграфов не всегда целесообразно – для ряда задач достаточно использовать простые графы и гиперграфы.
Целью настоящей работы являются математическое описание простых графов и гиперграфов в форме, удобной для их представления в реляционных БД, а также описание структуры реляционных БД, позволяющих адекватно отображать простые графы и гиперграфы и операции над ними за счет введения дополнительных объектов (ключи, индексы, триггеры), обеспечивающих ссылочную и доменную целостность БД.
Область применения полученных результатов – разработка ПО САПР, предназначенных для конструирования оборудования из типовых элементов (емкостные аппараты, теплообменники, колонны), проектирования технологических схем (подбор аппаратов, обеспечивающих выпуск продукта по заданной технологии, например, красителей в химической или молочных продуктов в пищевой промышленности), для размещения единиц оборудования в производственном помещении, например, аппаратов в цехе химического или станков в цехе машиностроительного предприятия.
Формальное описание простых графов с ограничениями
Обозначим простой граф G0(X, U), где X={xi}, – множество вершин графа, xi – i-я вершина графа; U={um(xi, xj)},
– множество вершин графа, xi – i-я вершина графа; U={um(xi, xj)},  ,
,  ,
, – множество ребер графа, um(xi, xj) – m-е ребро графа, соединяющее вершины xi и xj.
– множество ребер графа, um(xi, xj) – m-е ребро графа, соединяющее вершины xi и xj.
Ребро, соединяющее вершину саму с собой, um(xk, xk),  ,
,  , называется петлей. Простой граф не будет иметь петель, если выполняется ограничение
, называется петлей. Простой граф не будет иметь петель, если выполняется ограничение
O1: Ø$ um(xk, xk)ÎU, 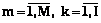 .
.
Если две вершины могут иметь несколько связывающих их ребер, то такой граф называется мультиграфом. Таким образом, простой граф не будет мультиграфом, если выполняется ограничение
O2: " um(xi, xj)ÎU, 
Ø$ ul(xi, xj)ÎU, l¹m,  .
.
Граф называется ориентированным, если ребро имеет направление, например, от xi (вершина-источник) к xj (вершина-приемник). Если вершина-приемник связана только одним ребром и только с одной вершиной-источником, то такой граф называется направленным деревом.
Введем ограничение O3, означающее, что вершина-приемник связана только с одной вершиной-источником (ограничения на число связей нет):
O3: " um(xi, xj)ÎU, 
Ø$ un(xk, xj)ÎU, n¹m, i¹k,  .
.
С учетом введенных ограничений граф будет направленным деревом, если одновременно выполняются условия O1, O2, O3.
 На рисунке 1 представлены примеры простых ориентированных графов.
На рисунке 1 представлены примеры простых ориентированных графов.
Добавим к классическому обозначению графа G(X, U) перечисленные выше ограничения. С учетом ограничений графы на рисунке 1 формально можно представить следующим образом:
1a: G(X, U, O1ÙO2ÙO3);
1б: G(X, U, O1ÙO3);
1в: G(X, U, O1ÙO2);
1г: G(X, U, O1);
1д: G(X, U, O1ÙO2).
Структура реляционной базы для описания простых графов с ограничениями
Реляционная БД (РБД) BDо, описывающая графы на рисунке 1, представляет собой кортеж ВDо=, где X, U, G – следующие отношения: X – вершины графа, U – ребра графа, G – граф (связи вершин и ребер).
В свою очередь, отношения X, U, G можно представить как
X={PK_ID_X, ID_X, Наименование_вершины}, где PK_ID_X – первичный ключ, ID_X – поле первичного ключа;
U={PK_ID_U, ID_U, Наименование_связи}, где PK_ID_U – первичный ключ; ID_U – поле первичного ключа;
G={PK_ID_G, FK_ID_U, FK_ID_XI, FK_ID_XJ, ID_G, ID_U, ID_XI, ID_XJ}, где PK_ID_G – первичный ключ; FK_ID_U, FK_ID_XI, FK_ID_XJ – внешние ключи (по полям ID_U, ID_XI, ID_XJ); ID_G – поле первичного ключа; ID_XI, ID_XJ – поля первичного ключа вершины-источника и вершины-приемника.
Так как ребро в графе всегда уникально, нет необходимости вводить отношение U, достаточно в отношение G добавить поле «Наименование_ связи». Тогда БД, описывающая графы (рис. 1), описывается двумя отношениями: ВDо=, где X={PK_ID_X, ID_X, Наименование_вершины}, G={PK_ID_G, FK_ID_XI, FK_ID_XJ, ID_G,ID_XI, ID_XJ, Наименование_связи}. Схема данных этой базы представлена на рисунке 2.
Описанная БД не включает ограничения O1, O2, O3. Внешние ключи FK_ID_XI, FK_ID_XJ гарантируют ссылочную целостность базы, то есть в таблице G не будет значений ID_XI и ID_XJ, не входящих в домен ID_X таблицы X. Ограничения O1, O2, O3 относятся к доменной целостности БД. Рассмотрим представление этих ограничений в БД BDо.
Проверка доменной целостности в РБД может осуществляться при выполнении операций удаления, редактирования и добавления записей.
Ограничение O1 – граф не должен иметь петель. Это означает, что в отношении G не может быть записи, у которой G.ID_XJ=G.ID_XI. Это ограничение может быть добавлено к BD следующим выражением:
alter table G add constraint
CK_O1 check (ID_XI<>ID_XJ). (1)
(Здесь и далее для представления программного кода используется Transact-SQL.)
Ограничение O2 – граф не является мультиграфом. Это ограничение может быть добавлено двумя способами:
а) добавлением к отношению G уникального индекса по полям ID_XI и ID_XJ:
create unique index IX_O2
on G (ID_XI, ID_XJ); (2)
б) проверкой истинности условия:
(not exists (select * from G
where G.ID_XI=@ID_XI
and G.ID_XJ = @ID_XJ )), (3)
где @ID_XI, @ID_XJ – значения G.ID_XI и G.ID_XJ добавляемой записи (или новые значения редактируемой записи).
Ограничение O3 – вершина-приемник связана только с одной вершиной-источником (ограничения на число связей нет). Это ограничение может быть нарушено при добавлении или редактировании записи. Ограничение O3 не будет нарушено, если добавляется ребро с вершиной-приемником, у которой нет связей, или связываются две вершины, у которых уже есть связь.
Обозначим @ID_XI, @ID_XJ значения G.ID_XI и G.ID_XJ добавляемой записи (или новые значения редактируемой записи). Тогда ограничение O3 не будет нарушено, если истинно выражение
(not exists (select * from G
where G.ID_XJ=@ID_XJ)) or
(exists (select * from G
where G.ID_XI=@ID_XI
and G.ID_XJ= @ID_XJ)). (4)
Выражения (1) и (2) создают отдельные объекты РБД, а именно, CK_O1, IX_O2. Выражения (3) и (4) могут проверять тригеры. Пометим тригеры, проверяющие выражения (3) и (4), как TR_O2 и TR_O3.
Обозначим G1={PK_ID_G, FK_ID_U, FK_ID_XI, FK_ID_XJ, ID_G, ID_U, ID_XI, ID_XJ}. Тогда с учетом ограничений таблица G для графов, представленных на рисунке 1, будет выглядеть следующим образом:
1a: G={G1, CK_O1, IX_O2 или TR_O2, TR_O3);
1б: G={G1, CK_O1, TR_O3};
1в: G={G1, CK_O1, IX_O2 или TR_O2};
1г: G={G1, CK_O1};
1д: G={G1, CK_O1, IX_O2 или TR_O2}.
Формальное описание неориентированных гиперграфов с ограничениями
 Обозначим гиперграф Gg(X, U), где X={xi},
Обозначим гиперграф Gg(X, U), где X={xi}, – множество вершин гиперграфа, xi – i-я вершина; U={um(Ym)},
– множество вершин гиперграфа, xi – i-я вершина; U={um(Ym)},  – множество ребер гиперграфа, um(Ym) – m-е ребро гиперграфа, Ym – множество вершин, инцидентных m-му ребру, YmÍX, Ym={xk}, kÎKm,
– множество ребер гиперграфа, um(Ym) – m-е ребро гиперграфа, Ym – множество вершин, инцидентных m-му ребру, YmÍX, Ym={xk}, kÎKm,  . При этом два множества вершин равны Ym=Yn, если у них одинаковое число элементов, то есть равны их мощности ½Ym½=½Yn½, и для любого элемента xkÎYm,
. При этом два множества вершин равны Ym=Yn, если у них одинаковое число элементов, то есть равны их мощности ½Ym½=½Yn½, и для любого элемента xkÎYm,  , во множестве Yn существует точно такой же элемент. Например, множества {x1, x5, x3} и {x3, x1, x5} равны.
, во множестве Yn существует точно такой же элемент. Например, множества {x1, x5, x3} и {x3, x1, x5} равны.
Примеры неориентированных гиперграфов представлены на рисунке 3.
Два ребра, имеющих одинаковые вершины, называются смежными. Гиперграф не будет иметь смежных ребер (рис. 3а), если выполняется ограничение O4: " um(Ym)ÎU; 
Ø$ un(Yn)ÎU;  ; n¹m; YmÇYn¹Æ.
; n¹m; YmÇYn¹Æ.
 На рисунке 3б представлен гиперграф, который используется в задачах размещения оборудования в производственных помещениях, когда определенная группа аппаратов (вершины) обладает одним и тем же свойством (первое ребро), например пожароопасность, и, следовательно, должна размещаться в соответствующем помещении (второе ребро). Описанная ситуация может быть учтена следующим ограничением. Определенный набор вершин YÍX инцидентен конкретному набору ребер U¢ÍU, причем нет вершин, принадлежащих Y, инцидентных ребрам другого набора вершин.
На рисунке 3б представлен гиперграф, который используется в задачах размещения оборудования в производственных помещениях, когда определенная группа аппаратов (вершины) обладает одним и тем же свойством (первое ребро), например пожароопасность, и, следовательно, должна размещаться в соответствующем помещении (второе ребро). Описанная ситуация может быть учтена следующим ограничением. Определенный набор вершин YÍX инцидентен конкретному набору ребер U¢ÍU, причем нет вершин, принадлежащих Y, инцидентных ребрам другого набора вершин.
O5: $U¢={up(Yp)}ÍU; YpÍX; 
Ø$ un(Yn)ÏU¢;  ; n¹p; YnÍX; YnÇYp¹Æ
; n¹p; YnÍX; YnÇYp¹Æ .
.
Ребра, имеющие равные множества вершин, называются кратными. Гиперграф не будет иметь кратных ребер (рис. 3в), если выполняется ограничение O6: " um(Ym)ÎU; 
Ø$ un(Yn)ÏU; m¹n;  ; Ym=Yn.
; Ym=Yn.
С учетом ограничений гиперграфы (рис. 3) можно записать в виде: 3a: Gg(X, U, O4); 3б: Gg(X, U, O5); 3в: Gg(X, U, O6).
Структура РБД для описания неориентированных гиперграфов с ограничениями
БД BDg, описывающая графы на рисунке 3, представляет собой следующий кортеж (схема данных показана на рисунке 4): ВDg=, где X, U, G – следующие отношения: X – вершины графа, U – ребра графа, G – граф (связи вершин и ребер).
В свою очередь, отношения X, U, G можно представить как X={PK_ID_X, ID_X, Наименование_вершины}, где PK_ID_X – первичный ключ, ID_X – поле первичного ключа; U={PK_ID_U, ID_U, Наименование_ребра}, где PK_ID_U – первичный ключ, ID_U – поле первичного ключа; G={PK_ID_G, FK_G_U, FK_G_X, ID_G, ID_U, ID_X}, где PK_ID_G – первичный ключ, FK_G_U, FK_G_X – внешние ключи (по полям ID_U, ID_X), ID_G – поле первичного ключа, ID_U, ID_X – поля первичного ключа ребра и вершины.
Внешние ключи FK_G_U, FK_G_X обеспечивают только ссылочную целостность данных и не обеспечивают выполнение ограничений O4, O5, O6. Рассмотрим способы представления ограничений O4, O5, O6 в РБД.
Ограничение O4 – гиперграф не должен иметь смежных ребер (рис. 3а). Это значит, что в отношении G может существовать только одна запись (кортеж) с заданной вершиной. Обозначим @ID_X значения G.ID_X добавляемой в G записи (или новое значение редактируемой записи). Ограничение O4 не будет нарушено, если истинно выражение
(not exists (select * from G
where G.ID_X=@ID_X )). (5)
 Вторым способом обеспечения выполнения ограничения O4 является создание уникального индекса в таблице G по полю ID_X:
Вторым способом обеспечения выполнения ограничения O4 является создание уникального индекса в таблице G по полю ID_X:
create unique index IX_O4 on G (ID_X).
Ограничение O5 – определенный набор вершин YÍX инцидентен определенному набору ребер U¢ÍU, причем нет вершин, принадлежащих Y, инцидентных ребрам другого набора (рис. 3б). Рассмотрим ситуации, при которых возможно нарушение ограничения O5.
Добавить (удалить) вершину в ребро. Обозначим @ID_U ребро, в которое добавляется вершина. Здесь возможны два случая:
а) если набор вершин корректируемого ребра инцидентен только одному ребру (ребро U5, рис. 3б), то вершина без проблем добавляется (удаляется) в ребро (ребро U5, рис. 3б). Набор вершин инцидентен только одному ребру @ID_U, если истинно условие
(not exists (select ID_U from G as b,
(select ID_X from G
where ID_U=@ID_U) as a
where b.ID_X=a.ID_X
and b.ID_U<>@ID_U); (6)
б) если набор вершин ребра инцидентен нескольким ребрам, то ограничение O5 не будет нарушено, если добавить (удалить) вершину ко всем этим ребрам. Для гиперграфа на рисунке 3б при добавлении новой вершины в ребро U1 необходимо добавить эту вершину также и в ребро U4. Предположим, надо добавить вершину @ID_X в ребро @ID_U, тогда команда добавления будет следующей:
insert into G (ID_X, ID_U)
(select distinct @ID_X, G.ID_U from G
inner join G as G1 on G1.ID_U=@ID_U
where G.ID_X=G1.ID_X). (7)
Добавить новое ребро. Обозначим X1={ID_X1, ID_X) таблицу вершин добавляемого ребра, @M1 – число вершин (число записей в X1). Добавить новое ребро можно
а) если все вершины X1 инцидентны хотя бы одному ребру (например, добавление ребра U3, когда существует ребро U2, рис. 3б). Все вершины X1 инцидентны хотя бы одному ребру, если истинно выражение @M1=@M2, где @M2 – число вершин существующего ребра, которые равны вершинам X1. Определение @M2 осуществляется выражением
select @M2=count(*) from G, X1,
(select top 1 ID_U from G, X1
where G.ID_X=X1.ID_X) as a
where G.ID_U=a.ID_U
and G.ID_X=X1.ID_X; (8)
б) если в G нет ни одной вершины из X1, то есть истинно выражение
(not exists (select G.ID_X from G,X1
where X1.ID_X=G.ID_X)). (9)
Ограничение O6 – гиперграф не должен иметь кратных ребер (рис. 3в). Рассмотрим следующие ситуации, которые могут привести к нарушению ограничения O6.
Добавить новое ребро. Обозначим вершины добавляемого ребра как отношение X1={ID_X}, @M1 – число вершин (число записей в X1). Добавить новое ребро можно
а) если хотя бы одна вершина из X1 не входит ни в одно ребро (не присутствует в G), то есть истинно выражение
(exists (select X1.ID_X from X1
where X1.ID_X not in
(select X1.ID_X from G,X1
where G.ID_X=X1.ID_X))); (10)
б) если не существует ребра c вершинами X1, то есть истинно выражение
(not exists (select count(*) from X1,G
where G.ID_X=X1.ID_X (11)
group by G.ID_U having (count(*))=@M1)).
Добавить вершину в ребро или удалить вершину из ребра. @ID_X обозначим ID_X добавляемой (удаляемой) вершины, @ID_U – ID_U корректируемого ребра.
Добавить вершину в ребро можно, если вершина не существует в G, то есть истинно выражение
(not exists (select * from G
where G.ID_X=@ID_X)). (12)
Добавить (удалить) вершину из ребра можно также, если нет ни одного ребра, все вершины которого равны вершинам получаемого ребра. Обозначим через X1 вершины получаемого ребра, тогда добавить (удалить) вершину из ребра можно, если выражение (11) истинно.
Обозначим TR_O4 триггер, осуществляющий проверку выражения (5) (ограничение 4), TR_O5 – триггер, осуществляющий проверку выполнимости ограничения O5 (выражения (6)–(9)), TR_O6 – триггер, осуществляющий проверку выполнимости ограничения O6 (выражения (10)–(12)).
Обозначим G1={PK_ID_G, FK_G_U, FK_G_X, ID_G, ID_U, ID_X}, тогда с учетом ограничений отношение G для графов (рис. 3) будет выглядеть следующим образом:
3а: G={G1, TR_O4 или IX_O4};
3б: G={G1, TR_O5};
3в: G={G1, TR_O6}.
В заключение отметим, что предложенное в работе формальное представление обычных графов и гиперграфов с ограничениями в виде теоретико-множественного описания удобно для последующего представления графов и гиперграфов в РБД. Описанные структура БД и дополнительные элементы (ключи, индексы, тригеры), предназначенные для описания обычных графов и гиперграфов с ограничениями, позволяют выполнять ограничения за счет сохранения ссылочной и доменной целостности базы. Представленные методы использовались авторами для создания программных шаблонов [5], предназначенных для разработки САПР технологического оборудования.
Литература
1. Овчинников В.А. Математические модели объектов задач структурного синтеза // Наука и образование: электрон. науч.-технич. изд. 2009. № 3. URL: http://technomag.edu.ru/doc/ 115712.html (дата обращения: 15.11.2010).
2. Овчинников В.А. Операции над ультра- и гиперграфами для реализации процедур анализа и синтеза структур сложных систем // Там же. № 10. URL: http://technomag.edu.ru/doc/ 132769.html (дата обращения: 15.11.2010).
3. Иванова Г.С. Способы представления структурных моделей // Там же. 2007. № 1. URL: http://technomag.edu.ru/doc/ 62742.html (дата обращения: 15.11.2010).
4. Мокрозуб В.Г. [и др.]. Применение N-ориентированных гиперграфов и реляционных баз данных для структурного и параметрического синтеза технических систем // Прикладная информатика. 2010. № 4 (28). С. 115–122.
5. Мокрозуб В.Г., Мариковская М.П., Красильников В.Е. Интеллектуальная автоматизированная система проектирования химического оборудования // Системы управления и информационные технологии. 2007. № 4.2(30). С. 264–267.
 – множество вершин графа, xi – i-я вершина графа; U={um(xi, xj)},
– множество вершин графа, xi – i-я вершина графа; U={um(xi, xj)},  ,
,  – множество ребер графа, um(xi, xj) – m-е ребро графа, соединяющее вершины xi и xj.
– множество ребер графа, um(xi, xj) – m-е ребро графа, соединяющее вершины xi и xj. ,
,  , называется петлей. Простой граф не будет иметь петель, если выполняется ограничение
, называется петлей. Простой граф не будет иметь петель, если выполняется ограничение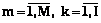 .
.
 .
.
 .
.
 Обозначим гиперграф Gg(X, U), где X={xi},
Обозначим гиперграф Gg(X, U), где X={xi}, . При этом два множества вершин равны Ym=Yn, если у них одинаковое число элементов, то есть равны их мощности ½Ym½=½Yn½, и для любого элемента xkÎYm,
. При этом два множества вершин равны Ym=Yn, если у них одинаковое число элементов, то есть равны их мощности ½Ym½=½Yn½, и для любого элемента xkÎYm, 
 ; n¹m; YmÇYn¹Æ.
; n¹m; YmÇYn¹Æ.

 .
. Вторым способом обеспечения выполнения ограничения O4 является создание уникального индекса в таблице G по полю ID_X:
Вторым способом обеспечения выполнения ограничения O4 является создание уникального индекса в таблице G по полю ID_X: