Journal influence
Bookmark
Next issue
Interface for study of sub-riemannian geodesics on 3d Lie groups
The article was published in issue no. № 4, 2012 [ pp. 200-203 ]Abstract:We consider a program interface for evaluation and study of geodesics of sub-Riemannian structures on groups SO(3) and SL(2), which was developed in Wolfram Mathematica. The given interface is the first step towards complete description of geodesic curves of all contact structures on 3-dimensional Lie groups. Equations for the adjoint variables of the Hamiltonian system are the same for all problems. In this paper equations for the Hamiltonian system of Pontryagin’s maximum principle for both cases are presented. Simulation results are demonstrated. Examples of geodesics on SO(3) and on SL(2) in elliptic and hyperbolic cases are shown.
Аннотация:Рассматривается программный интерфейс для вычисления и исследования геодезических субримановых структур на группах SO(3) и SL(2), разработанный в системе Wolfram Mathematica. Данный интерфейс является первым шагом к получению полного описания геодезических кривых всех контактных структур на трехмерных группах Ли. В статье приводятся уравнения гамильтоновой системы принципа максимума Понтрягина в обоих случаях. Уравнения для сопряженных переменных в гамильтоновой системе имеют один и тот же вид для всех задач. Продемонстрированы результаты работы программы. Показаны примеры геодезических на группах SO(3) и SL(2) в эллиптическом и гиперболическом случаях.
| Authors: (sachkov@sys.botik.ru) - , Ph.D, (i.beschastnyi@gmail.com) - , Russia, (sachkov@sys.botik.ru) - , (sachkov@sys.botik.ru) - | |
| Keywords: hamiltonian system, so(3), sl(2), wolfram mathematica, geodesic, sub-riemannian problem, interface |
|
| Page views: 11545 |
Print version Full issue in PDF (9.63Mb) Download the cover in PDF (1.26Мб) |
Субриманова геометрия является естественным языком теории управления [1]. На римановом многообразии касательный вектор к кривой может быть любым. В субримановом случае он должен лежать в определенном подпространстве. Совокупность всех этих подпространств называется распределением. Такое обобщение римановой геометрии имеет многочисленные приложения в различных областях науки и техники. Например, изопериметрические проблемы, такие как задача Дидоны, связаны с динамикой частиц в магнитном поле [2]. Задачи на группе вращений трехмерного пространства имеют приложения к задачам ориентации твердого тела, когда, например, вектор угловой скорости не покидает некоторую двухмерную плоскость [3]. Решения задач на специальных унитарных группах SU(2) и SU(3) используются в управлении квантовыми двухуровневыми и трехуровневыми системами [4, 5]. Задачи об эластиках Эйлера, оптимальном движении колесного робота и о восстановлении поврежденных изображений вариационным методом могут быть сформулированы как соответствующие задачи на группе движений евклидова пространства [1, 6, 7]. Многие механические задачи с неголономными ограничениями допускают субриманово описание, например, задача о качении шара по плоскости [6]. Помимо этого, с помощью субримановой геометрии могут быть получены аппроксимации нелинейных систем управления, сохраняющие свойство управляемости [8], которые находят применение, к примеру, при управлении колесным роботом с прицепами [9]. В этой статье рассматриваются субримановы структуры на специальной ортогональной группе SO(3) и специальной линейной группе SL(2):
Распределение на этих группах задается как линейная оболочка пары независимых векторных полей span{f1, f2} [10], а параметризация геодезических получается как решение соответствующей задачи оптимального управления:
где q=q(t) – кривая на группе; ui – управления; fi(q) – левоинвариантные векторные поля. Рассматриваемые субримановы структуры возникают в задачах восстановления изображений, а также в задачах управления вращением твердого тела в пространстве. Для исследования поставленной задачи используются принцип максимума Понтрягина и численные методы интегрирования обыкновенных дифференциальных уравнений. Гамильтонова система принципа максимума Понтрягина В работе [10] описана классификация левоинвариантных субримановых задач (1) на трехмерных группах Ли. Показано, что основное семейство таких задач в некотором каноническом репере {f0, f1, f2} удовлетворяет условиям [f1, f0]=(sina+ +cosa)f2, [f2, f0]=(sina–cosa)f1, [f2, f1]=f0, где [fi, fj] – коммутатор векторных полей; параметр aÎ(0, p). Из принципа максимума Понтрягина [1] получена гамильтонова система дифференциальных уравнений, которой удовлетворяют оптимальные траектории q(t) в задаче оптимального управле- ния (1):
Здесь g, c – сопряженные переменные принципа максимума Понтрягина. Запишем в координатах дифференциальное уравнение (3) для следующих случаев. 1. Случай
2. Случай
3. Случай
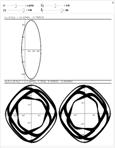
Из-за высокой сложности гамильтоновой системы (2), (3) для ее решения и исследования необходимо применение компьютерных методов. Интерфейс для вычисления и исследования геодезических Для численного интегрирования гамильтоновой системы (2), (3) использовалась программная среда Wolfram Mathematica [10]. Соответствующие функции вычисления геодезических для каждой субримановой задачи были запрограммированы и объединены в общий интерфейс. Входными параметрами интерфейса являются переменные a, g0, c0, t1, которые задаются с помощью управляющих ползунков. Выходными параметрами являются значение вектора сопряженных переменных в конечной точке g(t1), c(t1), график проекции геодезической на фазовую плоскость маятника (g, c)(t), tÎ[0, t1], значение конечной точки в некоторых координатах (для SO(3) компоненты кватерниона q0, q1, q2, q3, а для SL(2) компо- ненты матрицы a, b, c, d) и проекция геодезических (в случае SO(3) на сферу x2+y2+z2=1, а в случае SL(2) – на плоскости (a, b) и (c, d)). Интерфейс удобен как средство компьютерного исследования семейства задач оптимального управления (1), он может использоваться и математиками, и инженерами, работающими с приложениями этих задач в обработке изображений и механике. Примеры графиков, иллюстрирующие работу интерфейса, приведены на рисунках 1–4.
В заключение отметим, что основными результатами данной работы являются гамильтонова система (2), (3) принципа максимума Понтрягина для субримановой задачи (1), координатное представление системы (2), программный интерфейс для исследования субримановой задачи (1). Разработанный интерфейс целесообразно использовать при изучении субримановых структур на трехмерных группах Ли. Изображения геодезических и их проекций позволяют предположить наличие дискретных симметрий (отражений) в этих задачах. При разных значениях параметра a можно наблюдать разное качественное поведение геодезических во времени, например, асимптотическое поведение, ограниченность, наличие точек возврата и огибающих в проекции. Применяя интерфейс, можно сравнивать свойства геодезических для разных классов задач (эллиптического и гиперболического случаев для группы SL(2)). Эта информация будет полезной для последующего изучения рассматриваемых задач. В дальнейшем планируется математическое исследование субримановых структур на трехмерных группах Ли: параметризация геодезических, описание симметрий экспоненциального отображения и соответствующих множеств Максвелла для оценки верхней границы времени разреза и первого сопряженного времени. Это позволит дополнить программный интерфейс функциями управления оптимальными траекториями, которые будут использованы в задачах восстановления изображений и управления вращениями твердого тела в пространстве. Литература 1. Аграчев А.А., Сачков Ю.Л. Геометрическая теория управления. М.: Физматлит, 2005. 392 с. 2. Agrachev A.A., Gauthier J.-P.A. On the Dido problem and plane Isoperimetric problems. Acta Applicandae Mathematicae, 1999, no. 57, pp. 287–338. 3. Арнольд В.И. Математические методы классической механики. М.: Эдиториал УРСС, 2000. 408 с. 4. Boscain U., Mason P. Time minimal trajectories for a spin ½ particle in a magnetic field. Journ. of Mathematical Physics. 2006, no. 47. 5. Boscain U., Chambrion T., Sigalotti M. Nonisotropic 3-level quantum systems: complete solutions for minimum time and minimal energy. Discrete and Continuous Dynamical Systems-B. 2005. Vol. 5. Iss. 4, pp. 957–990. 6. Jurdjevic V. Geometric Control Theory. Cambridge University Press, 1997. 510 p. 7. Сачков Ю.Л., Ардентов А.А., Маштаков А.П. Параллельный алгоритм и программа восстановления изофот поврежденных изображений // Программные системы: теория и приложения. 2010. Т. 1. № 1. С. 3–20. 8. Agrachev A.A.. Sarychev A.V. Filtrations of a Lie algebra of vector fields and the nilpotent approximation of controllable systems. Dokl. Akad. Nauk SSSR, 1987. Vol. 295. no. 4, pp. 777–781. 9. Маштаков А.П.. Алгоритмическое и программное обеспечение решения конструктивной задачи управления неголономными пятимерными системами // Программные системы: теория и приложения. 2012. Т. 1. № 3. C. 3–29. 10. Agrachev A., Barilari D. Sub-Riemannian structures on 3D Lie groups. Journ. of Dynamical and Control Systems, 2012, Vol. 18, pp. 21–44. 11. Wolfram Mathematica 8, URL: http://www.wolfram.com/ mathematica/ (дата обращения: 13.10.2012). |
| Permanent link: http://swsys.ru/index.php?id=3342&lang=en&page=article |
Print version Full issue in PDF (9.63Mb) Download the cover in PDF (1.26Мб) |
| The article was published in issue no. № 4, 2012 [ pp. 200-203 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Применение образцов проектирования графического интерфейса для реализации навигационных функций
- Аппаратно-программный комплекс диагностики состояния ионосферы по характеристикам сигналов радиопередатчиков диапазона очень низких частот
- Разработка ядра интегрированной информационной системы
- Применение Interactive Data Language для обработки данных радиометрических измерений
- Программное обеспечение подсистемы контроля качества выпускаемой продукции с использованием интеллектуальных алгоритмов
Back to the list of articles

 (1)
(1) (2)
(2) (3)
(3) соответствует группе SO(3), которая параметризуется кватернионом единичной длины (q0, q1, q2, q3). Получим:
соответствует группе SO(3), которая параметризуется кватернионом единичной длины (q0, q1, q2, q3). Получим:
 соответствует группе SLh(2), которая задается матрицами
соответствует группе SLh(2), которая задается матрицами  с единичным определителем. Получим:
с единичным определителем. Получим:
 соответствует группе SLe(2), которая задается матрицами
соответствует группе SLe(2), которая задается матрицами