Одним из актуальных направлений совершенствования средств измерений является реализация функций самостоятельной оценки метрологического состояния измерительных приборов в процессе эксплуатации. В работе [1] и на сайте http://yokogawa.ru/conceptbusiness показана принципиальная возможность создания термопреобразователя сопротивления, поддерживающего эту функцию. Так как в процессе эксплуатации прибора непосредственно измеряемой величиной является сопротивление, необходимо разработать метод, позволяющий оценивать температурные погрешности по результатам измерения сопротивлений. Математическая модель, описывающая зависимость температурных величин от измеренных сопротивлений, имеет вид системы уравнений, левая часть которых представлена в виде полиномов, а правая часть содержит эталонные температурные значения. Коэффициенты полиномов, а также степени полиномов заранее не определены. Таким образом, для разработки метода, позволяющего осуществлять оценку собственного состояния средства измерения, требуется решить задачу параметрической идентификации модели, называемую задачей идентификации калибровочных коэффициентов. Решение поставленной задачи и оценку температурных погрешностей выполняют в процессе калибровки прибора. В работе [2] установлено, что при решении этой задачи малые погрешности исходных данных оказывают существенное влияние на погрешность получаемого результата, поэтому при разработке алгоритмов ее решения необходимо использовать методы регуляризации.
В данной статье описаны алгоритмы определения коэффициентов в задаче параметрической идентификации и моделирования значений температуры по результатам измерения сопротивлений двумя термометрами из различных металлов, а также алгоритм оценки погрешностей полученных температур. Эталоном послужила математическая модель зависимости температуры от сопротивлений, возникающая при оценке собственного состояния преобразователя температуры с двумя термосопротивлениями, приведенная в работе [3]. Алгоритм решения задачи параметрической идентификации основан на использовании метода регуляризации Тихонова для решения плохо обусловленных систем линейных уравнений.
Кроме того, описан программно-вычислительный комплекс для построения и тестирования различных эталонных моделей. Вычислительный комплекс создан в среде MatLab и основан на функционально-модульном принципе. Приведены иллюстрации основной части пользовательского интерфейса. Разработанный комплекс послужил основой для обработки экспериментальных данных.
Алгоритм идентификации коэффициентов
Пусть входные сигналы R, t есть векторные функции, состоящие из n³3 компонент Rk, tk,  . Известно, что в эталонной модели значения tk измерены с некоторой погрешностью, уровень которой не превосходит d, поэтому число d тоже рассматривается как входной сигнал. Искомые коэффициенты являются компонентами функции A=(Am, Am-1, …, A1, A0), где количество компонент заранее неизвестно. Таким образом, необходимо определить и значение числа m.
. Известно, что в эталонной модели значения tk измерены с некоторой погрешностью, уровень которой не превосходит d, поэтому число d тоже рассматривается как входной сигнал. Искомые коэффициенты являются компонентами функции A=(Am, Am-1, …, A1, A0), где количество компонент заранее неизвестно. Таким образом, необходимо определить и значение числа m.
Согласно [3], эталонная модель, характеризующая зависимость температуры t от сопротивления R, описывается системой
 (1)
(1)
Задача параметрической идентификации для (1) состоит в определении степени полиномов m и коэффициентов A=(Am, Am-1, …, A1, A0).
Так как эталоном послужила математическая модель, описывающая зависимость температуры от сопротивления в задаче оценки собственного состояния преобразователя температуры с двумя термосопротивлениями, задачу параметрической идентификации необходимо решать для двух наборов входных данных ( t, d) и (
t, d) и ( t, d), в которых число d и функция t одинаковы.
t, d), в которых число d и функция t одинаковы.
Для решения задачи идентификации коэффициентов потребуем, чтобы функция t удовлетворяла условиям tk Î[a, b] и
a=t1
Входные сигналы  и
и  задаются по формулам, приведенным в работе [3]:
задаются по формулам, приведенным в работе [3]:
 , (3)
, (3)
 , (4)
, (4)
где tk – температура;  ,
,  – коэффициенты первого сенсора, а
– коэффициенты первого сенсора, а 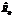
 – второго сенсора, заданные соответствующими ГОСТами (например ГОСТ Р 8.625–2006).
– второго сенсора, заданные соответствующими ГОСТами (например ГОСТ Р 8.625–2006).
Алгоритм решения задачи параметрической идентификации для системы (1) применяется для каждого сенсора и состоит из нескольких этапов. На первом этапе выделим ненулевые компоненты функции A=(Am, Am-1, …, A1, A0). Для этого введем матрицу
 . (5)
. (5)
Из теоремы Кронекера–Капелли следует, что система (1) имеет решение, если ранг r матрицы (5) удовлетворяет неравенству r£n, поэтому на начальном шаге алгоритма полагаем m=n–1. Далее находим ранг матрицы (5), выделив линейно-независимые столбцы методом Жордана–Гаусса с выбором главного элемента. Наибольший номер ненулевого столбца m(d) определяет старшую степень полиномов в системе (1), а номера линейно-независимых столбцов соответствуют ненулевым компонентам функции A=(Am, Am-1, …, A1, A0) системы (1).
Затем из линейно-независимых столбцов матрицы (5) формируем новую матрицу  . Представим систему (1) в эквивалентном виде:
. Представим систему (1) в эквивалентном виде:
 (6)
(6)
Система (6) является переопределенной, ее правая часть задана с погрешностью, а число обусловленности матрицы  достаточно велико, поэтому для решения системы необходимо использовать методы регуляризации.
достаточно велико, поэтому для решения системы необходимо использовать методы регуляризации.
Перейдем к поиску регуляризованного решения A(a, d)=(Am(d), Am(d)-1, …,  ) системы (6), устойчивого относительно погрешностей исходных данных. Для этого используем регуляризующий алгоритм, основанный на введении стабилизирующего функционала [4]. Согласно такому подходу, в качестве регуляризованного решения системы (6) возьмем решение системы
) системы (6), устойчивого относительно погрешностей исходных данных. Для этого используем регуляризующий алгоритм, основанный на введении стабилизирующего функционала [4]. Согласно такому подходу, в качестве регуляризованного решения системы (6) возьмем решение системы
 ,
,
где  – матрица, сопряженная к
– матрица, сопряженная к  ; a – параметр регуляризации, выбранный по принципу невязки:
; a – параметр регуляризации, выбранный по принципу невязки:

Так как алгоритм идентификации коэффициентов реализуется для двух наборов сигналов: ( t, d) и (
t, d) и ( t, d), наборы выходных сигналов, полученные в результате вычислений, обозначим
t, d), наборы выходных сигналов, полученные в результате вычислений, обозначим  и
и 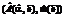 соответственно.
соответственно.
Замечание. В качестве наборов входных сигналов ( , t, d) и (
, t, d) и ( , t, d) возможно использование экспериментальных данных.
, t, d) возможно использование экспериментальных данных.
Проверим достоверность результата в задаче параметрической идентификации коэффициентов. В силу специфики эталонной модели процедура проверки выполняется совместно для всех обрабатываемых наборов сигналов.
Алгоритм проверки достоверности результата и оценки температурных погрешностей
Входными сигналами являются наборы  и
и 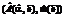 , полученные в результате применения алгоритма идентификации коэффициентов, и векторная функция t, состоящая из n³3 компонент tk,
, полученные в результате применения алгоритма идентификации коэффициентов, и векторная функция t, состоящая из n³3 компонент tk,  .
.
Для проверки достоверности результата и оценки температурных погрешностей выполним моделирование температурных функций  и
и  а также функций измеренных сопротивлений
а также функций измеренных сопротивлений  и
и  .
.
Подставим наборы  и
и 
 в систему (1) и найдем компоненты
в систему (1) и найдем компоненты  и
и 
 , функций
, функций  и
и  . Затем подставим компоненты
. Затем подставим компоненты  в уравнение (3), а
в уравнение (3), а  в (4) и вычислим значения компонент
в (4) и вычислим значения компонент  и
и  ,
,  для функций
для функций  и
и  соответственно.
соответственно.
С целью проверки введем для каждого сенсора величины r1 и r2, характеризующие уровни допустимых погрешностей измерения соответствующих сопротивлений. Процедуры вычисления r1 и r2 регламентированы ГОСТами (ГОСТ Р 8.625–2006), и для данного алгоритма эти значения являются константами. В качестве проверочных функций используем величины  и
и  , определяемые формулами:
, определяемые формулами:
 , (7)
, (7)
 . (8)
. (8)
Отметим, что нормы, стоящие в правых частях (7) и (8), согласуются с методикой вычисления значений r1 и r2.
Если  и
и  , то проверка считается успешной и принимается решение о том, что наборы
, то проверка считается успешной и принимается решение о том, что наборы  и
и 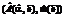 удовлетворяют требованиям, предъявляемым к решению задачи идентификации калибровочных коэффициентов системы (1) при заданных пользователем исходных данных.
удовлетворяют требованиям, предъявляемым к решению задачи идентификации калибровочных коэффициентов системы (1) при заданных пользователем исходных данных.
Перейдем к оценке температурных погрешностей. С этой целью используем функции 
 ,
,  ,
,  а также функцию
а также функцию  Величины
Величины 
 и DT определяются формулами
и DT определяются формулами
 ,
,  , (9)
, (9)
 ,
,  , (10)
, (10)
 (11)
(11)
 .
.
Такой подход к выбору функций оценки обусловлен требованиями, предъявляемыми к работе термопреобразователя на этапе калибровки.
Используя формулы (9)–(11), находим значения функций  ,
,  и DT=e. Если величины e1 и e2 находятся в пределах соответствующих классов допусков, то процесс калибровки термопреобразователя считается успешным. В этом случае величина e определяет допустимую температурную погрешность при эксплуатации данного преобразователя.
и DT=e. Если величины e1 и e2 находятся в пределах соответствующих классов допусков, то процесс калибровки термопреобразователя считается успешным. В этом случае величина e определяет допустимую температурную погрешность при эксплуатации данного преобразователя.
Программно-вычислительный комплекс для калибровки термометров сопротивления
С целью проверки эффективности построенных алгоритмов и получения оценок температурных погрешностей создан программный комплекс, реализующий эталонную модель. Эталоном послужило описание зависимости температуры от сопротивлений в задаче оценки собственного состояния преобразователя температуры с двумя термометрами сопротивления [4]. В качестве выходных данных рассматривались калибровочные коэффициенты  и
и  , а также величины критериев (9)–(11). Программный комплекс создан в среде MatLab, основан на модульном принципе и включает в себя
, а также величины критериев (9)–(11). Программный комплекс создан в среде MatLab, основан на модульном принципе и включает в себя
– модуль построения моделей эталонных температур и эталонных сопротивлений для входных сигналов по формулам (3) и (4);
– модуль идентификации, реализующий алгоритм решения задачи параметрической идентификации калибровочных коэффициентов;
– модуль проверки достоверности результатов и оценки температурных погрешностей.
Архитектура системы показана на рисунке 1.
 В блоке настройки входных данных пользователь имеет возможность в диалоговом режиме вводить следующие параметры эталонной модели: границы температурного диапазона, необходимого для моделирования функций t,
В блоке настройки входных данных пользователь имеет возможность в диалоговом режиме вводить следующие параметры эталонной модели: границы температурного диапазона, необходимого для моделирования функций t,  и
и  количество измерений, а также допустимый уровень температурной погрешности. Далее пользователь отправляет команду активизации блока моделирования, в котором осуществляется моделирование эталонной температуры t и эталонных сопротивлений
количество измерений, а также допустимый уровень температурной погрешности. Далее пользователь отправляет команду активизации блока моделирования, в котором осуществляется моделирование эталонной температуры t и эталонных сопротивлений  и
и  Значения эталонных сопротивлений и температур записываются в отдельном файле. После завершения работы блока моделирования автоматически активируется блок идентификации.
Значения эталонных сопротивлений и температур записываются в отдельном файле. После завершения работы блока моделирования автоматически активируется блок идентификации.
В блоке идентификации реализуется алгоритм решения задачи параметрической идентификации (1) для каждого набора входных данных. Результатом работы блока являются значения компонент функций  и
и 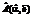 . Выходные данные блока записываются в файл.
. Выходные данные блока записываются в файл.
Далее автоматически активируется блок валидации и оценки погрешностей, в котором моделируются значения из- меренных температур  и
и  а также вычисляются значения функций
а также вычисляются значения функций  и
и  определяемые формулами (7) и (8). Если значения
определяемые формулами (7) и (8). Если значения  и
и  превышают заданный уровень погрешности, то пользователь получает сообщение о невозможности корректного решения задачи при введенных начальных данных. Если значения функций
превышают заданный уровень погрешности, то пользователь получает сообщение о невозможности корректного решения задачи при введенных начальных данных. Если значения функций  и
и  находятся в допустимых пределах, то вычисляются значения температурных погрешностей, определяемые формулами (9)–(11). В случае успешного завершения работы блока валидации компоненты функций измеренных температур и величины найденных температурных погрешностей записываются в файл, содержащий значения калибровочных коэффициентов.
находятся в допустимых пределах, то вычисляются значения температурных погрешностей, определяемые формулами (9)–(11). В случае успешного завершения работы блока валидации компоненты функций измеренных температур и величины найденных температурных погрешностей записываются в файл, содержащий значения калибровочных коэффициентов.
 После этого калибровочные коэффициенты и температурные погрешности выводятся в диалоговое окно, используемое ранее для ввода исходных данных. В блоке визуализации предусмотрена возможность графического изображения значений эталонных и измеренных сопротивлений.
После этого калибровочные коэффициенты и температурные погрешности выводятся в диалоговое окно, используемое ранее для ввода исходных данных. В блоке визуализации предусмотрена возможность графического изображения значений эталонных и измеренных сопротивлений.
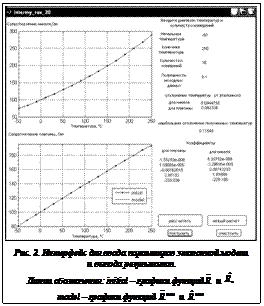
Пользовательский интерфейс включает в себя диалоговое окно (рис. 2) и графическое изображение функций температурных погрешностей (рис. 3). Ввод температурного диапазона, количества измерений, допустимой погрешности, а также вывод значений найденных коэффициентов и величин температурных погрешностей e1, e2, e реализован в форме диалогового окна. В этом же окне графически иллюстрируются результаты моделирования эталонных 
 и измеренных сопротивлений
и измеренных сопротивлений  ,
, 
На рисунке 2 приведен пример диалогового окна, иллюстрирующий результаты отдельного вычислительного эксперимента.
Графики величин температурных погрешностей, полученных в результате этого эксперимента, изображены на рисунке 3. По горизонтальной оси этого рисунка отмечены значения температур, а по вертикальной – величины температурных погрешностей (°C).
 Созданный программный комплекс используется для исследования характеристик эталонной модели. Изменяя входные данные, пользователь получает информацию об устойчивости решений, возможном уровне температурных погрешностей, о влиянии количества измерений на результаты вычислений. Вся информация, полученная в результате исследований, хранится в соответствующих файлах на диске и может быть использована для подробного ознакомления и анализа.
Созданный программный комплекс используется для исследования характеристик эталонной модели. Изменяя входные данные, пользователь получает информацию об устойчивости решений, возможном уровне температурных погрешностей, о влиянии количества измерений на результаты вычислений. Вся информация, полученная в результате исследований, хранится в соответствующих файлах на диске и может быть использована для подробного ознакомления и анализа.
В заключение отметим, что в статье предложены алгоритмы решения задачи идентификации коэффициентов и оценки температурных погрешностей для обработки информации при калибровке термометров сопротивления. Описанные алгоритмы могут быть использованы для обработки информации других средств измерения, использующих эталонную модель, аналогичную (1). На основании представленных алгоритмов разработан программно-вычислительный комплекс и проведен вычислительный эксперимент. Для адаптации ПО к обработке экспериментальных данных вместо блока настройки и визуализации используется блок обработки информации, хранящейся в БД.
Литература
1. Белоусов М.Д., Шестаков А.Л. Метод принятия решения в процессе работы о выходе термометра сопротивления за предел допускаемой погрешности // Вестн. Южно-Уральского гос. ун-та: сер. Компьютерные технологии, управление, радиоэлектроника. 2011. № 23 (240). С. 19–25.
2. Белоусов М.Д., Шестаков А.Л., Япарова Н.М. Оценка собственного состояния термометров сопротивлений // Вестн. Южно-Уральского гос. ун-та: сер. Компьютерные технологии, управление, радиоэлектроника. 2012. № 3. С. 105–109.
3. Япарова Н.М., Белоусов М.Д., Шестаков А.Л. Использование регуляризующего алгоритма для определения коэффициентов в задаче оценки собственного состояния термометров сопротивления // Вестн. Южно-Уральского гос. ун-та: сер. Компьютерные технологии, управление, радиоэлектроника. 2012. № 3. С. 45–49.
4. Тихонов А.Н., Арсенин В.Я. Методы решения некорректно поставленных задач. М.: Наука, 1986. 288 с.
Referens
1. Belousov M.D, Shestakov A.L. Decision-making on-stream method of the RTD thermoreceiver about the limit of error excess. Vestnik Yuzhno-Uralskogo gos. un-ta. Ser. Kompyuternye tekhnologii, upravlenie, radioelektronika [The bulletin of South Ural State Univ. Series Computer technologies, management, electronics]. 2011, vol. 23 (240), pp. 19–25 (in Russ.).
2. Belousov M.D., Shestakov A.L., Yaparova N.M. Estimation of resistive thermometers eigenstate. Vestnik Yuzhno-Uralskogo gos. un-ta. Ser. Kompyuternye tekhnologii, upravlenie, radioelektronika [The bulletin of South Ural State Univ. Series Computer technologies, management, electronics]. 2012, vol. 3, pp. 105–109 (in Russ.).
3. Yaparova N.M., Belousov M.D, Shestakov A.L. The use of regularizing algorithm for coefficient estimation in the problem of resistive thermometers condition assessment. Vestnik Yuzhno-Uralskogo gos. un-ta. Ser. Kompyuternye tekhnologii, upravlenie, radioelektronika [The bulletin of South Ural State Univ. Series Computer technologies, management, electronics]. 2012, vol. 3, pp. 45–49 (in Russ.).
4. Tikhonov A.N., Arsenin V.Ya. Metody resheniya nekorrektno postavlennykh zadach [Methods for solving ill-posed problems]. Moscow, Nauka Publ., 1986, 288 p.
 . Известно, что в эталонной модели значения tk измерены с некоторой погрешностью, уровень которой не превосходит d, поэтому число d тоже рассматривается как входной сигнал. Искомые коэффициенты являются компонентами функции A=(Am, Am-1, …, A1, A0), где количество компонент заранее неизвестно. Таким образом, необходимо определить и значение числа m.
. Известно, что в эталонной модели значения tk измерены с некоторой погрешностью, уровень которой не превосходит d, поэтому число d тоже рассматривается как входной сигнал. Искомые коэффициенты являются компонентами функции A=(Am, Am-1, …, A1, A0), где количество компонент заранее неизвестно. Таким образом, необходимо определить и значение числа m. (1)
(1) t, d) и (
t, d) и ( t, d), в которых число d и функция t одинаковы.
t, d), в которых число d и функция t одинаковы. и
и  задаются по формулам, приведенным в работе [3]:
задаются по формулам, приведенным в работе [3]: , (3)
, (3) , (4)
, (4) ,
,  – коэффициенты первого сенсора, а
– коэффициенты первого сенсора, а 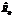
 – второго сенсора, заданные соответствующими ГОСТами (например ГОСТ Р 8.625–2006).
– второго сенсора, заданные соответствующими ГОСТами (например ГОСТ Р 8.625–2006). . (5)
. (5) . Представим систему (1) в эквивалентном виде:
. Представим систему (1) в эквивалентном виде: (6)
(6) ) системы (6), устойчивого относительно погрешностей исходных данных. Для этого используем регуляризующий алгоритм, основанный на введении стабилизирующего функционала [4]. Согласно такому подходу, в качестве регуляризованного решения системы (6) возьмем решение системы
) системы (6), устойчивого относительно погрешностей исходных данных. Для этого используем регуляризующий алгоритм, основанный на введении стабилизирующего функционала [4]. Согласно такому подходу, в качестве регуляризованного решения системы (6) возьмем решение системы ,
, – матрица, сопряженная к
– матрица, сопряженная к 
 и
и 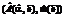 соответственно.
соответственно. и
и  а также функций измеренных сопротивлений
а также функций измеренных сопротивлений  и
и  .
.
 в систему (1) и найдем компоненты
в систему (1) и найдем компоненты  и
и 
 и
и  . Затем подставим компоненты
. Затем подставим компоненты  в (4) и вычислим значения компонент
в (4) и вычислим значения компонент  и
и  ,
,  для функций
для функций  и
и  , определяемые формулами:
, определяемые формулами: , (7)
, (7) . (8)
. (8) и
и  , то проверка считается успешной и принимается решение о том, что наборы
, то проверка считается успешной и принимается решение о том, что наборы 
 ,
,  ,
,  Величины
Величины 
 и DT определяются формулами
и DT определяются формулами ,
,  ,
,  (11)
(11) ,
,  и DT=e. Если величины e1 и e2 находятся в пределах соответствующих классов допусков, то процесс калибровки термопреобразователя считается успешным. В этом случае величина e определяет допустимую температурную погрешность при эксплуатации данного преобразователя.
и DT=e. Если величины e1 и e2 находятся в пределах соответствующих классов допусков, то процесс калибровки термопреобразователя считается успешным. В этом случае величина e определяет допустимую температурную погрешность при эксплуатации данного преобразователя. и
и  , а также величины критериев (9)–(11). Программный комплекс создан в среде MatLab, основан на модульном принципе и включает в себя
, а также величины критериев (9)–(11). Программный комплекс создан в среде MatLab, основан на модульном принципе и включает в себя
 Значения эталонных сопротивлений и температур записываются в отдельном файле. После завершения работы блока моделирования автоматически активируется блок идентификации.
Значения эталонных сопротивлений и температур записываются в отдельном файле. После завершения работы блока моделирования автоматически активируется блок идентификации.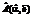 . Выходные данные блока записываются в файл.
. Выходные данные блока записываются в файл. определяемые формулами (7) и (8). Если значения
определяемые формулами (7) и (8). Если значения  После этого калибровочные коэффициенты и температурные погрешности выводятся в диалоговое окно, используемое ранее для ввода исходных данных. В блоке визуализации предусмотрена возможность графического изображения значений эталонных и измеренных сопротивлений.
После этого калибровочные коэффициенты и температурные погрешности выводятся в диалоговое окно, используемое ранее для ввода исходных данных. В блоке визуализации предусмотрена возможность графического изображения значений эталонных и измеренных сопротивлений.

 Созданный программный комплекс используется для исследования характеристик эталонной модели. Изменяя входные данные, пользователь получает информацию об устойчивости решений, возможном уровне температурных погрешностей, о влиянии количества измерений на результаты вычислений. Вся информация, полученная в результате исследований, хранится в соответствующих файлах на диске и может быть использована для подробного ознакомления и анализа.
Созданный программный комплекс используется для исследования характеристик эталонной модели. Изменяя входные данные, пользователь получает информацию об устойчивости решений, возможном уровне температурных погрешностей, о влиянии количества измерений на результаты вычислений. Вся информация, полученная в результате исследований, хранится в соответствующих файлах на диске и может быть использована для подробного ознакомления и анализа.