В последние годы вызывает интерес разработка методов, связанных с моделированием железнодорожных перевозок [1], с построением расписаний перевозок и управлением транспортными системами [2, 3], а также принципов построения автоматизированных систем управления железнодорожным транспортом [4, 5].
Привлекает внимание и разработка методов, позволяющих определять подходящие маршруты доставки грузовых вагонов от станций отправления к станциям назначения с проходящими гру- зовыми поездами, а также выбирать наиболее выгодные маршруты движения поездов. Такой интерес вызван тем, что определение маршрутов доставки грузовых вагонов от станций отправления к станциям назначения позволит железнодорожным службам наилучшим образом развозить грузы по железнодорожной сети, а в случае необходимости исключать ненужные маршруты, что обеспечит более эффективную доставку грузов заказчикам.
Однако решение задач определения наиболее подходящих маршрутов доставки грузовых вагонов с проходящими грузовыми поездами, а также выбора наиболее выгодных маршрутов движения поездов вызывает затруднения из-за их большой размерности и сложности ограничений, накладываемых на условия доставки вагонов. Поэтому требуются специальные модели и методы.
В данной работе рассматриваются принципы построения моделей и методов, позволяющих решать подобные задачи. Они основаны на опи- сании изменений количества вагонов в составе каждого поезда после прохождения станций и на каждой станции после прохождения поездов с помощью специальных уравнений движения. Рассматриваются также структура и принципы построения компьютерной системы, в которой были реализованы разработанные модели и методы. Вычислительные эксперименты, проводимые с этой системой, подтвердили ее работоспособность и достаточно высокую эффективность.
Постановка задач
Рассмотрим сначала постановку задачи определения маршрутов доставки грузовых вагонов от станций отправления к станциям назначения.
Пусть дана железнодорожная сеть G, включающая M сортировочных станций. На каждой станции находится определенное количество грузовых вагонов, которые требуется доставить к станциям назначения проходящими грузовыми поездами.
Доставка вагонов может осуществляться как одним, так и несколькими поездами путем прицепки соответствующего количества вагонов к поезду, проходящему через станцию отправки, и отцепки нужного количества вагонов на станциях назначения или на промежуточных сортировочных станциях, где эти вагоны будут прицепляться к другим поездам, следующим через эту сортировочную станцию позже. С помощью таких поездов ожидающие отправки вагоны доставляются к станциям назначения или на наиболее удобные станции для последующей доставки проходящими поездами на станции назначения.
Для железнодорожной сети G задана информация о Q поездах, проходящих по сети. О маршруте каждого поезда q известны стоимость его выполнения cq, станция и время отправления, сортировочные станции, через которые поезд проходит по маршруту, время прибытия на них и отправления, а также конечная станция маршрута и время прибытия на нее.
Известны доход  получаемый за доставку вагона h-й категории ценности и f-й весовой категории с l-й станции на j-ю, весовая категория f каждого перевозимого вагона, определяющая его вес pf, а также штраф
получаемый за доставку вагона h-й категории ценности и f-й весовой категории с l-й станции на j-ю, весовая категория f каждого перевозимого вагона, определяющая его вес pf, а также штраф 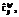 выставляемый за срыв доставки одного вагона h-й категории ценности и f-й весовой категории со станции отправления l на станцию назначения j. В каждый поезд может быть включено не более L вагонов с грузами, а вес перевозимых вагонов не может превышать заданную величину P.
выставляемый за срыв доставки одного вагона h-й категории ценности и f-й весовой категории со станции отправления l на станцию назначения j. В каждый поезд может быть включено не более L вагонов с грузами, а вес перевозимых вагонов не может превышать заданную величину P.
В задаче требуется таким образом определить маршруты движения каждого вагона с проходящими поездами от станции отправления до станции назначения, чтобы максимизировать доходы от доставки вагонов с грузами заказчикам и минимизировать количество перецепок вагонов с одного поезда на другой, а также минимизировать штрафы за вагоны, которые не удалось доставить.
Рассмотрим теперь постановку другой задачи, в которой требуется определить необходимое количество поездов для доставки грузовых вагонов по железнодорожной сети заданной конфигурации.
Исходные данные для нее аналогичны данным, используемым в предыдущей задаче. В задаче нужно из множества поездов выбрать такие, которые позволят при минимальных затратах на выполнение маршрутов движения доставить грузовые вагоны от станций отправления к станциям назначения по железнодорожной сети известной конфигурации. Кроме этого, необходимо определить количество вагонов, которые следует включать в состав каждого поезда на сортировочных станциях и отцеплять на станциях назначения или на промежуточных станциях для включения в другие поезда, чтобы обеспечить доставку вагонов от станций отправки до станций назначения. В случае невозможности обеспечить доставку всех заказанных вагонов к станциям назначения требуется минимизировать штрафы за вагоны, которые не удалось доставить.
Принципы построения моделей
Для решения первой из поставленных задач строится оптимизационная модель, принципы формирования которой основаны на использовании идей теории математического программирования [6–8] и управления дискретными процессами [9, 10].
В соответствии с этими принципами изменение количества вагонов в составе каждого поезда после прохождения сортировочной станции описывается с помощью уравнений движения, ко- торые строятся по аналогии с используемыми в теории и методах управления дискретными системами и процессами и в данном случае имеют следующий вид:
 ,
,
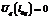 ,
,  , (1)
, (1)
 , l=1, …, nq, (2)
, l=1, …, nq, (2)
где Uq(l+1) – количество вагонов в поезде  после отправки с l-й станции; Uq(l) − количество вагонов в поезде
после отправки с l-й станции; Uq(l) − количество вагонов в поезде  перед прибытием на l-ю станцию;
перед прибытием на l-ю станцию;  − количество вагонов, подцепляемых к поезду q на l-й станции;
− количество вагонов, подцепляемых к поезду q на l-й станции;  − количество вагонов, отцепляемых от поезда q на l-й станции;
− количество вагонов, отцепляемых от поезда q на l-й станции;  − количество вагонов в поезде q на станции, являющейся станцией отправления для q-го поезда; L − максимальное количество вагонов, которое может содержать любой поезд, где
− количество вагонов в поезде q на станции, являющейся станцией отправления для q-го поезда; L − максимальное количество вагонов, которое может содержать любой поезд, где  − станция отправления q-го поезда, nq − конечная станция маршрута q-го поезда.
− станция отправления q-го поезда, nq − конечная станция маршрута q-го поезда.
Ограничения (2) определяют максимальное количество вагонов, которое может быть в каждом поезде.
Кроме количества вагонов в q-м поезде, необходима также информация о станции отправления и назначения каждого вагона в поезде, а также о ценности и весе вагона. Эта информация необходима для отцепки нужных вагонов на станции, через которую проходит поезд, и включения в состав поезда вагонов, ожидающих на станции отправки, чтобы не нарушить ограничения на вес поезда и доставить на станции назначения наиболее ценные вагоны, если все вагоны доставить не удается.
Количество и типы грузовых вагонов в составе q-го поезда после прохождения l-й станции из-за перецепки вагонов на станции меняется, и эти изменения можно учесть с помощью уравнений динамики, строящихся по аналогии с уравнениями (1) и имеющих в этом случае вид:
 ,
,

 ,
,  , (3)
, (3)
где  − количество вагонов h-й категории ценности и f-й весовой категории каждого перевозимого вагона в составе q-го поезда после станции l, для которых r-я станция является станцией отправления, а j-я станция – станцией назначения;
− количество вагонов h-й категории ценности и f-й весовой категории каждого перевозимого вагона в составе q-го поезда после станции l, для которых r-я станция является станцией отправления, а j-я станция – станцией назначения;  − количество вагонов h-й категории ценности и f-й весовой категории в составе q-го поезда перед станцией l, для которых r-я станция является станцией отправления, а j-я станция – станцией назначения;
− количество вагонов h-й категории ценности и f-й весовой категории в составе q-го поезда перед станцией l, для которых r-я станция является станцией отправления, а j-я станция – станцией назначения;  − количество вагонов h-й категории ценности и f-й весовой категории, которые прицепляются к q-му поезду на станции l для их доставки с r-й станции на станцию назначения j;
− количество вагонов h-й категории ценности и f-й весовой категории, которые прицепляются к q-му поезду на станции l для их доставки с r-й станции на станцию назначения j;  − количество вагонов h-й категории ценности и f-й весовой категории, которые отцепляются от q-го поезда на станции l для их доставки с r-й станции на станцию назначения j.
− количество вагонов h-й категории ценности и f-й весовой категории, которые отцепляются от q-го поезда на станции l для их доставки с r-й станции на станцию назначения j.
Грузоподъемность вагонов в каждом поезде не должна превышать заданной величины P, поэтому в модель включается следующее ограничение:
 , (4)
, (4)
где pf − вес вагона f-й весовой категории.
Ограничения на переменные  имеют следующий вид:
имеют следующий вид:
 , (5)
, (5)
где  − множество станций, на которые могут быть доставлены вагоны поездом q с l-й станции как до станций назначения, так и до станций, с которых эти вагоны могут быть доставлены к станциям назначения другими поездами;
− множество станций, на которые могут быть доставлены вагоны поездом q с l-й станции как до станций назначения, так и до станций, с которых эти вагоны могут быть доставлены к станциям назначения другими поездами;  − множество станций, от которых вагоны могут быть доставлены на l-ю станцию другими поездами для дальнейшей доставки поездом q к станциям назначения или к станциям, с которых эти вагоны могут быть доставлены к станциям назначения другими поездами.
− множество станций, от которых вагоны могут быть доставлены на l-ю станцию другими поездами для дальнейшей доставки поездом q к станциям назначения или к станциям, с которых эти вагоны могут быть доставлены к станциям назначения другими поездами.
Ограничения на переменные  будут иметь следующий вид:
будут иметь следующий вид:
 , (6)
, (6)
где  − множество станций, на которые могут быть доставлены вагоны, отцепленные от поезда q на l-й станции, другими поездами до станции назначения или станций, с которых вагоны могут быть доставлены к станциям назначения.
− множество станций, на которые могут быть доставлены вагоны, отцепленные от поезда q на l-й станции, другими поездами до станции назначения или станций, с которых вагоны могут быть доставлены к станциям назначения.
Уравнения, определяющие изменения в количестве грузовых вагонов на станциях после прохождения поездов, строятся так же, как и уравнения динамики в теории управления дискретными процессами. Однако динамика в изменении количества грузовых вагонов на станциях после прохождения поездов в отличие от ранее рассмотренных уравнений динамики определяется порядком прохождения каждой станции поездами разных маршрутов. Поэтому эти уравнения удобно записать в виде
 ,
,
 ,
,  , (7)
, (7)
где  − количество вагонов h-й категории ценности и f-й весовой категории, которые надо доставить с r-й станции на станцию назначения j, и находящиеся на станции l перед прибытием на нее поезда q, следующего через нее k-м по порядку прохождения; Nl − количество поездов, маршруты которых проходят через станцию l.
− количество вагонов h-й категории ценности и f-й весовой категории, которые надо доставить с r-й станции на станцию назначения j, и находящиеся на станции l перед прибытием на нее поезда q, следующего через нее k-м по порядку прохождения; Nl − количество поездов, маршруты которых проходят через станцию l.
Оптимизируемый функционал для такой модели может быть представлен в следующем виде:


 , (8)
, (8)
где a1, a2, a3 − весовые коэффициенты;  − затраты на отцепку вагонов от одного поезда на сортировочных станциях для ожидания нужного поезда и на прицепку к этому поезду;
− затраты на отцепку вагонов от одного поезда на сортировочных станциях для ожидания нужного поезда и на прицепку к этому поезду;  − штраф за срыв доставки одного вагона h-й категории ценности и f-й весовой категории со станции отправления l на станцию назначения j.
− штраф за срыв доставки одного вагона h-й категории ценности и f-й весовой категории со станции отправления l на станцию назначения j.
С использованием первой группы слагаемых, имеющих весовой коэффициент a1, в этом функционале максимизируется доход от доставки вагонов заказчикам. Минимизация второй группы слагаемых с весовым коэффициентом a2 позволяет по возможности сократить количество перецепок вагонов с одного поезда на другой. Минимизация третьей группы слагаемых с весовым коэффициентом a3 позволяет по возможности сократить штрафы за вагоны, которые не удалось доставить заказчикам.
Переменные Ulq, 





 неотрицательны и выбираются таким образом, чтобы максимизировать доход, получаемый от доставки вагонов от станций отправления до станций назначения, и минимизировать затраты на количество перецепок на станциях, где вагоны дожидаются подходящих поездов, а также штрафы за вагоны, которые не удалось доставить на станции назначения.
неотрицательны и выбираются таким образом, чтобы максимизировать доход, получаемый от доставки вагонов от станций отправления до станций назначения, и минимизировать затраты на количество перецепок на станциях, где вагоны дожидаются подходящих поездов, а также штрафы за вагоны, которые не удалось доставить на станции назначения.
Расчеты этой модели сводятся к решению задачи целочисленного линейного программирования. В результате расчета модели определяется количество вагонов, которые следует подцеплять к каждому поезду и отцеплять от него на станциях по маршруту поезда. Кроме того, определяется количество вагонов, которые ожидают подходящие поезда на станциях, находящихся на пересечении маршрутов движения разных поездов, а также количество вагонов, которые не удалось доставить.
Фактически в задаче определяется маршрут движения каждого вагона. При этом выполняются ограничения на количество и вес вагонов в каждом поезде, а также на количество вагонов на станциях, на которых происходит перецепка вагонов с одного поезда на другой.
Рассмотрим теперь принципы построения модели для расчетов второй задачи, в которой требуется определить необходимое количество поездов для доставки грузовых вагонов со станций отправления к станциям назначения.
Эта модель строится на таких же принципах, что и для расчетов первой задачи. Для опреде- ления необходимого количества поездов в железнодорожной сети заданной конфигурации для доставки грузов экспертами сначала формируется избыточное количество маршрутов движения поездов. Затем в результате расчета модели из-за ограничений на стоимость выполнения маршрутов движения поездов в сети будет оставлено нужное количество. Расчеты такой модели также сводятся к решению задачи целочисленного линейного программирования.
Изменение количества вагонов в составе поезда q после прохождения сортировочной станции l описывается с помощью уравнений движения, аналогичных уравнениям (1). Однако ограничения на количество вагонов в поезде q для данной задачи имеют следующий вид:
 ,
,  l=1, …, nq,(9)
l=1, …, nq,(9)
где zq − булевы переменные типа {0, 1}. Величина zq равна 1, если маршрут поезда q включен в расписание движения по железнодорожной сети G, и нулю, если включение поезда q в расписание движения нецелесообразно.
Остальные ограничения данной модели будут аналогичны ограничениям (2)–(7). Оптимизируемый функционал для этой модели имеет следующий вид:


 , (10)
, (10)
где ai − весовые коэффициенты (i=1, …, 4); bq − стоимость движения поезда q по соответствующему маршруту на железнодорожной сети.
В результате расчета будут определены маршруты движения поездов, которые следует сох- ранить в железнодорожной сети, количество ва- гонов, которые следует подцеплять к каждому поезду и отцеплять от него на станциях маршрута поезда, а также количество вагонов, не доставленных клиентам.
Все переменные модели – zq, 

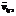




 – неотрицательны. Они выбираются таким образом, чтобы максимизировать доход, получаемый от доставки вагонов от станций отправления до станций назначения, и минимизировать затраты на количество маршрутов движения поездов в сети и количество перецепок вагонов на станциях, а также на штрафы за вагоны, которые не удалось доставить на станции назначения.
– неотрицательны. Они выбираются таким образом, чтобы максимизировать доход, получаемый от доставки вагонов от станций отправления до станций назначения, и минимизировать затраты на количество маршрутов движения поездов в сети и количество перецепок вагонов на станциях, а также на штрафы за вагоны, которые не удалось доставить на станции назначения.
Программная реализация системы
Компьютерную систему, позволяющую решать рассмотренные выше задачи, предлагается строить по модульному принципу. Каждый модуль такой системы выполняет определенные функции. Наглядное представление системы управления вагонопотоками дано на рисунке. В состав системы включены модули
– ввода исходных данных;
– выбора моделей решения описанных выше задач;
– расчета сформированных моделей;
– автоматизации движения вагонов;
– сбора, хранения и отображения информации, полученной в результате расчетов моделей и редактирования маршрутов.
 Модуль ввода исходных данных предназначен для ввода и преобразования данных в формат, который используется в пакете численных методов оптимизации GLPK (GNU Linear Programming Kit), предназначенном для решения задач линейного программирования, в том числе с целочисленными и булевыми переменными. Введенные данные сохраняются в БД системы и используются остальными модулями системы по мере необходимости. В БД модуля хранится информация о конфигурации железнодорожной сети, количестве вагонов, которые необходимо доставить от станций отправления до станций назначения. Также в БД сохраняется информация о поездах сети, их начальных, промежуточных и конечных станциях.
Модуль ввода исходных данных предназначен для ввода и преобразования данных в формат, который используется в пакете численных методов оптимизации GLPK (GNU Linear Programming Kit), предназначенном для решения задач линейного программирования, в том числе с целочисленными и булевыми переменными. Введенные данные сохраняются в БД системы и используются остальными модулями системы по мере необходимости. В БД модуля хранится информация о конфигурации железнодорожной сети, количестве вагонов, которые необходимо доставить от станций отправления до станций назначения. Также в БД сохраняется информация о поездах сети, их начальных, промежуточных и конечных станциях.
Модуль формирования и выбора моделей, предназначенных для решения описанных выше задач, используется для настройки режимов работы системы и выбора требуемой модели. В модуле содержатся текстовые файлы с символьным описанием соотношений модели, записанные на языке, используемом в пакете численных методов оптимизации GLPK. Ввод числовых значений параметров производится из БД системы.
Модуль расчета сформированных моделей включает пакет численных методов оптимизации GLPK. Помимо стандартного набора алгоритмов для решения задач линейного программирования с непрерывными переменными, пакет позволяет решать задачи с целочисленными и булевыми переменными методом ветвей и границ в сочетании с различными вариантами методов отсечений. Кроме того, пакет включает реализацию метода внутренней точки (primal-dualinterior-point), который оказывается эффективным при решении некоторых задач линейного программирования большой размерности. Пакет оснащен развитым и хорошо документированным С API; это позволяет встраивать численные методы GLPK в другие приложения и управлять ходом вычислений, что особенно важно для нестандартных режимов работы метода ветвей и границ. Пакет GLPK поддерживает ввод исходных данных на языке GNU MathProg в форматах MPS и CPLEX LP. Единый архив (с исходными кодами и документацией) содержит все необходимые конфигурационные файлы, позволяющие скомпилировать GLPK для основных вычислительных платформ: Linux x86_32/64, Windows XP (и более поздние) с 32- и 64-битной архитектурой (для компилятора Visual C версий 9 и 10). Важной особенностью применения GLPK в грид-системах является его возможность работать в режиме командной строки. Вне грид-сети GLPK чаще используется в консольном режиме в форме исполняемого файла glpsol (на Linux) или glpsol.exe (на Windows), реже – как динамически подключаемая, например к MATLAB, библиотека процедур. Для создания GLPK-грид применялся консольный вариант пакета.
Модуль автоматизации движения вагонов используется для сбора и анализа полученных результатов расчета модели. С его помощью могут редактироваться некоторые маршруты движения поездов и вагонов, а также выбираться поезда из множества, которые позволят при минимальных затратах на выполнение маршрутов движения доставить грузовые вагоны по железнодорожной сети.
Модуль хранения результатов расчетов предназначен для записи, хранения, анализа и дальнейшего использования результатов расчета моделей. Результаты расчетов доступны в текстовых файлах, сохраняется и журнал работы пакета. В модуле предусматривается возможность редактирования некоторых маршрутов движения поездов и вагонов.
Результаты вычислительных экспериментов
С использованием предложенных в статье моделей было решено более двадцати задач, связанных с определением маршрута движения каждого вагона, а также количества вагонов, которые следует подцеплять и отцеплять от поездов на всех станциях маршрута. В задачах также требовалось определить количество вагонов, которые ожидают подходящие поезда на станциях, находящихся на пересечении маршрутов движения разных поездов, а также количество вагонов, не доставленных заказчикам.
Кроме этого, было решено около десятка задач, связанных с определением маршрутов поездов, которые следует сохранить в железнодорожной сети, и количества вагонов, которые нужно подцеплять и отцеплять от каждого поезда на всех станциях маршрута.
Проведенные расчеты задач показали, что с использованием разработанных моделей удается достаточно быстро определять маршруты доставки грузовых вагонов от станций отправления к станциям назначения с проходящими грузовыми поездами, а также определять маршруты поездов, которые следует сохранить в железнодорожной сети.
Результаты использования предлагаемых моделей и пакета численных методов оптимизации GLPK можно увидеть на примере решения следующей задачи.
Пусть задана железнодорожная сеть, включающая 40 сортировочных станций. На каждой станции находится заданное количество грузовых вагонов от 0 до 30 штук, которые требуется доставить к станциям назначения с проходящими через станцию грузовыми поездами. Для каждого вагона известен доход, получаемый от его доставки на станцию назначения, и штраф за невозможность доставки. В соответствии с заданным расписанием и маршрутами по сети совершают свои рейсы шесть поездов. Известны станция и время отправления каждого поезда, сортировочные станции, через которые он проходит по маршруту, время прибытия на них и отправления от них, а также станция назначения и время прибытия на нее. В состав каждого поезда может входить не более 45 вагонов.
Необходимо определить маршруты движения каждого вагона с проходящими поездами от станции отправления до станции назначения таким образом, чтобы максимизировать доходы от доставки вагонов с грузами заказчикам и минимизировать количество перецепок вагонов с одного поезда на другой, а также штрафы за недоставленные вагоны. Расчеты задачи использовали 337 Mб оперативной памяти и заняли 55 секунд. В результате решения были определены маршруты движения каждого вагона с проходящими поездами, станции, на которых производилась их перецепка с одного поезда на другой, если это требовалось, а также вагоны, которые не удалось доставить на станции назначения.
Разработка принципов и методов решения подобных задач важна и актуальна. Формулируя их как задачи оптимизации с различными критериями, можно получать наиболее выгодные маршруты движения вагонов с различными поездами путем их перецепки на соответствующих сортировочных станциях, что, в свою очередь, позволит сократить время доставки грузов заказчикам. Кроме того, разработка принципов построения подобных моделей и методов их расчета позволит моделировать перспективные направления развития железнодорожных сетей, определять наиболее выгодные маршруты движения грузовых поездов при имеющихся заказах на отправку и получение грузов, а также обеспечивать более эффективное использование железнодорожной сети, организуя в случае необходимости дополнительные маршруты движения поездов.
Литература
1.Лазарев А.А., Мусатова Е.Г., Кварацхелия А.Г., Гафа- ров Е.Р. Теория расписаний. Задачи управления транспортными системами. М.: Изд-во МГУ, 2012. 159 с.
2.Тарасов А.С., Рубцов А.О. Моделирование железнодорожных перевозок на территории России // Тр. ИСА РАН. 2009. Т. 46. С. 274–278.
3.Лазарев А.А., Гафаров Е.Р. Теория расписаний. Задачи и алгоритмы. М.: Изд-во МГУ, 2011. 222 с.
4.Елисеев С.Ю., Соснов Д.А. Концепция построения автоматизированной системы управления // Железнодорожный транспорт. 2004. № 4. С. 32–35.
5.Осьминин А.Т., Анисимов В.А., Клюев Н.А., Осьминин Л.А., Анисимов В.В. Об автоматизации разработки графика движения // Железнодорожный транспорт. 2012. № 4. С. 19–24.
6.Поляк Б.Т. Введение в оптимизацию. М.: Наука, 1983. 382 с.
7.Галеев Э.М. Оптимизация. М.: ЛИБРОКОМ, 2010. 336 с.
8.Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации. М.: Наука, 1986. 328 с.
9.Пропой А.И. Элементы теории оптимальных дискретных процессов. М.: Наука, 1973. 256 с.
10. Болтянский В.Г. Оптимальное управление дискретными системами. М.: Наука, 1973. 446 с.
References
1. Lazarev A.A., Musatova E.G., Kvaratskheliya A.G., Gafarov E.R. Teoriya raspisany. Zadachi upravleniya tran-sportnymi sistemami [The Theory of Scheduling. The Problems of Transport Systems Management]. MSU Publ., 2012,
159 p.
2. Tarasov A.S., Rubtsov A.O. The modeling of freight routes in Russia. Trudy ISA RAN [Proc. of the ISA RAS]. 2009,
vol. 46, pp. 274–278 (in Russ.).
3. Lazarev A.A., Gafarov E.R. Teoriya raspisany. Zadachi i algoritmy [The Theory of Scheduling. Tasks and Algo-rithms]. MSU Publ., 2011, 222 p.
4. Eliseev S.Yu., Sosnov D.A. The сoncept of creating an automated control system. Zheleznodorozhny transport
[Railway Transport]. 2004, no. 4, pp. 32–35 (in Russ.).
5. Osminin A.T., Anisimov V.A., Klyuev N.A., Osminin L.A., Anisimov V.V. About the automation of development of
the schedule. Zheleznodorozhny transport [Railway Transport]. 2012, no. 4, pp. 19–24 (in Russ.).
6. Polyak B.T. Vvedenie v optimizatsiyu [Introduction in Optimization]. Nauka Publ., 1983, pp. 382.
7. Galeev E.M. Optimizatsiya [Optimization]. LIBROKOM Publ., 2010, pp. 336.
8. Sukharev A.G., Timokhov A.V., Fedorov V.V. Kurs metodov optimizatsii [The Сourse of Optimization Methods].
Nauka Publ., 1986, pp. 328.
9. Propoy A.I. Elementy teorii optimalnykh diskretnykh protsessov [The Elements of the Optimum Discrete Processes
Theory]. Nauka Publ., 1973, 256 p.
10. Boltyanskiy V.G. Optimalnoe upravlenie diskretnymi sistemami [The Optimum Control of Discrete Systems]. Nauka
Publ., 1973, 446 p.
 получаемый за доставку вагона h-й категории ценности и f-й весовой категории с l-й станции на j-ю, весовая категория f каждого перевозимого вагона, определяющая его вес pf, а также штраф
получаемый за доставку вагона h-й категории ценности и f-й весовой категории с l-й станции на j-ю, весовая категория f каждого перевозимого вагона, определяющая его вес pf, а также штраф 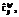 выставляемый за срыв доставки одного вагона h-й категории ценности и f-й весовой категории со станции отправления l на станцию назначения j. В каждый поезд может быть включено не более L вагонов с грузами, а вес перевозимых вагонов не может превышать заданную величину P.
выставляемый за срыв доставки одного вагона h-й категории ценности и f-й весовой категории со станции отправления l на станцию назначения j. В каждый поезд может быть включено не более L вагонов с грузами, а вес перевозимых вагонов не может превышать заданную величину P. ,
,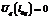 ,
,  , (1)
, (1) , l=1, …, nq, (2)
, l=1, …, nq, (2) после отправки с l-й станции; Uq(l) − количество вагонов в поезде
после отправки с l-й станции; Uq(l) − количество вагонов в поезде  − количество вагонов, подцепляемых к поезду q на l-й станции;
− количество вагонов, подцепляемых к поезду q на l-й станции;  − количество вагонов, отцепляемых от поезда q на l-й станции;
− количество вагонов, отцепляемых от поезда q на l-й станции;  − количество вагонов в поезде q на станции, являющейся станцией отправления для q-го поезда; L − максимальное количество вагонов, которое может содержать любой поезд, где
− количество вагонов в поезде q на станции, являющейся станцией отправления для q-го поезда; L − максимальное количество вагонов, которое может содержать любой поезд, где  − станция отправления q-го поезда, nq − конечная станция маршрута q-го поезда.
− станция отправления q-го поезда, nq − конечная станция маршрута q-го поезда. ,
, 
 ,
,  , (3)
, (3) − количество вагонов h-й категории ценности и f-й весовой категории каждого перевозимого вагона в составе q-го поезда после станции l, для которых r-я станция является станцией отправления, а j-я станция – станцией назначения;
− количество вагонов h-й категории ценности и f-й весовой категории каждого перевозимого вагона в составе q-го поезда после станции l, для которых r-я станция является станцией отправления, а j-я станция – станцией назначения;  − количество вагонов h-й категории ценности и f-й весовой категории в составе q-го поезда перед станцией l, для которых r-я станция является станцией отправления, а j-я станция – станцией назначения;
− количество вагонов h-й категории ценности и f-й весовой категории в составе q-го поезда перед станцией l, для которых r-я станция является станцией отправления, а j-я станция – станцией назначения;  − количество вагонов h-й категории ценности и f-й весовой категории, которые прицепляются к q-му поезду на станции l для их доставки с r-й станции на станцию назначения j;
− количество вагонов h-й категории ценности и f-й весовой категории, которые прицепляются к q-му поезду на станции l для их доставки с r-й станции на станцию назначения j;  − количество вагонов h-й категории ценности и f-й весовой категории, которые отцепляются от q-го поезда на станции l для их доставки с r-й станции на станцию назначения j.
− количество вагонов h-й категории ценности и f-й весовой категории, которые отцепляются от q-го поезда на станции l для их доставки с r-й станции на станцию назначения j. , (4)
, (4) имеют следующий вид:
имеют следующий вид: , (5)
, (5) − множество станций, на которые могут быть доставлены вагоны поездом q с l-й станции как до станций назначения, так и до станций, с которых эти вагоны могут быть доставлены к станциям назначения другими поездами;
− множество станций, на которые могут быть доставлены вагоны поездом q с l-й станции как до станций назначения, так и до станций, с которых эти вагоны могут быть доставлены к станциям назначения другими поездами;  − множество станций, от которых вагоны могут быть доставлены на l-ю станцию другими поездами для дальнейшей доставки поездом q к станциям назначения или к станциям, с которых эти вагоны могут быть доставлены к станциям назначения другими поездами.
− множество станций, от которых вагоны могут быть доставлены на l-ю станцию другими поездами для дальнейшей доставки поездом q к станциям назначения или к станциям, с которых эти вагоны могут быть доставлены к станциям назначения другими поездами. будут иметь следующий вид:
будут иметь следующий вид: , (6)
, (6) − множество станций, на которые могут быть доставлены вагоны, отцепленные от поезда q на l-й станции, другими поездами до станции назначения или станций, с которых вагоны могут быть доставлены к станциям назначения.
− множество станций, на которые могут быть доставлены вагоны, отцепленные от поезда q на l-й станции, другими поездами до станции назначения или станций, с которых вагоны могут быть доставлены к станциям назначения. ,
, ,
,  , (7)
, (7) − количество вагонов h-й категории ценности и f-й весовой категории, которые надо доставить с r-й станции на станцию назначения j, и находящиеся на станции l перед прибытием на нее поезда q, следующего через нее k-м по порядку прохождения; Nl − количество поездов, маршруты которых проходят через станцию l.
− количество вагонов h-й категории ценности и f-й весовой категории, которые надо доставить с r-й станции на станцию назначения j, и находящиеся на станции l перед прибытием на нее поезда q, следующего через нее k-м по порядку прохождения; Nl − количество поездов, маршруты которых проходят через станцию l.

 , (8)
, (8) − затраты на отцепку вагонов от одного поезда на сортировочных станциях для ожидания нужного поезда и на прицепку к этому поезду;
− затраты на отцепку вагонов от одного поезда на сортировочных станциях для ожидания нужного поезда и на прицепку к этому поезду;  − штраф за срыв доставки одного вагона h-й категории ценности и f-й весовой категории со станции отправления l на станцию назначения j.
− штраф за срыв доставки одного вагона h-й категории ценности и f-й весовой категории со станции отправления l на станцию назначения j.





 неотрицательны и выбираются таким образом, чтобы максимизировать доход, получаемый от доставки вагонов от станций отправления до станций назначения, и минимизировать затраты на количество перецепок на станциях, где вагоны дожидаются подходящих поездов, а также штрафы за вагоны, которые не удалось доставить на станции назначения.
неотрицательны и выбираются таким образом, чтобы максимизировать доход, получаемый от доставки вагонов от станций отправления до станций назначения, и минимизировать затраты на количество перецепок на станциях, где вагоны дожидаются подходящих поездов, а также штрафы за вагоны, которые не удалось доставить на станции назначения. ,
,  l=1, …, nq,(9)
l=1, …, nq,(9) , (10)
, (10)

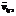




 – неотрицательны. Они выбираются таким образом, чтобы максимизировать доход, получаемый от доставки вагонов от станций отправления до станций назначения, и минимизировать затраты на количество маршрутов движения поездов в сети и количество перецепок вагонов на станциях, а также на штрафы за вагоны, которые не удалось доставить на станции назначения.
– неотрицательны. Они выбираются таким образом, чтобы максимизировать доход, получаемый от доставки вагонов от станций отправления до станций назначения, и минимизировать затраты на количество маршрутов движения поездов в сети и количество перецепок вагонов на станциях, а также на штрафы за вагоны, которые не удалось доставить на станции назначения.
