Внедрение конкурентных отношений на рынке электроэнергии требует решения ряда новых задач, например, о доле участия каждой станции в снабжении конкретной нагрузки и определении потоков мощности, текущих от каждого генератора по ветвям схемы замещения электрической сети, то есть какие генераторы снабжают конкретного потребителя, какая величина мощности каждого генератора передается по конкретным линиям электропередачи и какие потери мощности обусловлены передачей электроэнергии от каждого генератора к конкретной нагрузке.
В концепции конкурентного оптового рынка электроэнергии принято считать, что в интегрированной электроэнергетической системе (ЭЭС) невозможно проследить маршруты поставки электроэнергии от конкретного поставщика к конкретному потребителю. Однако в конце прошлого века в научных публикациях были предложены алгоритмы, основанные на использовании направлений потоков мощности и принципа пропорциональности [1–6].
Положенный в основу этих алгоритмов принцип пропорциональности основан на предположении, что в любом узле электрической сети каждая единица мощности выходит из узла в такой же пропорции [1], в какой мощность входит в этот узел.
Определение адресности является важным также для оценки
- показателей использования электрической сети различными участниками рынка;
- абонентской платы за пользование сетью вдоль пути протекания мощности;
- ответственности источников и потребителей электроэнергии за соблюдение режима (нахождение переменных режима в заданных технологических пределах);
- изменения топологии схемы сети таким образом, чтобы вся или большая часть производимой на определенной станции мощности поступала определенному потребителю: алгоритм адресности в этом случае будет определять эффективность принимаемых решений (при заключении прямых контрактов между производителем и потребителем на передачу электроэнергии);
- локальных балансов реактивной мощности.
В последние годы появилось большое число публикаций, использующих как матричные, так и графовые алгоритмы решения задачи адресности. Решение проблемы адресности, использующее матричный подход, получено в [1].
Решение проблемы адресности реактивной мощности позволяет проследить пути передачи ре- активной мощности от генераторов: проанализировать эффективность использования имеющихся в системе и установки дополнительных компенсирующих устройств.
 На рисунке 1 приведена блок схема решения задачи адресности потоков мощности.
На рисунке 1 приведена блок схема решения задачи адресности потоков мощности.
Прослеживание путей передачи мощности в сети может быть выполнено против их потоков, то есть от нагрузок к генераторам (прямое отслеживание), или вдоль потоков, то есть от генераторов к нагрузкам (обратное отслеживание).
Распределение активных мощностей без учета потерь
Задача определения коэффициентов адресности по значениям перетоков и инъекции активной или реактивной мощности является линейной задачей, использующей 1-й закон Кирхгофа. Прослеживание путей передачи мощности в сети может быть выполнено против их потоков, то есть от нагрузок к генераторам, или вдоль потоков, то есть от генераторов к нагрузкам.
Первый закон Кирхгофа можно представить в матричной форме: M ´ IB+ J = 0, где IВ – матрица токов ветвей; J – матрица узловых (задающих) токов.
При решении задачи адресности электрическая сеть представляется в виде ориентированного графа, являющегося совокупностью узлов и ветвей, связанных между собой.
Рассмотрим сеть, состоящую из n узлов и m ветвей, и определим РУ как (n´1)-вектор узловых потоков мощностей (то есть сумма из узловых притоков или оттоков, включая местную генерацию и нагрузку соответственно), PGГ как (n´1)-вектор узловых генераций, PН как (n´1)-вектор узловых нагрузок, PВ как (m´1)-вектор потоков ветвей.
Для решения задачи адресности необходимо записать исходные данные, которые будут использоваться в расчете, а именно: столбцовые матрицы задающих генерирующих мощностей РГ, задающих нагрузочных мощностей РН, потоков мощностей в каждой ветви электрической сети PВ. Если узел генераторный, то записывается значение генерации, в других случаях значения равны нулю.
Первая матрица инциденции M, составленная для всех узлов схемы, включая и балансирующий узел, задает конфигурацию электрической сети. Число строк матрицы M равно количеству узлов, включая и балансирующий, а число столбцов соответствует количеству ветвей в сети. Таким образом, первая матрица инциденций M устанавливает взаимосвязь между узлами и ветвями направлен- ного графа сети. Каждый элемент матрицы Mis, находящийся на пересечении i-й строки, соответствующей i-му узлу, и s-го столбца, соответствующего (i–j)-й ветви, равен:
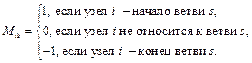
Первая матрица инциденций M может быть представлена в виде суммы двух матриц [1]:
M=Mпр+Mоб, (1)
где Mпр – матрица соединения ветвей во всех узлах схемы, элементами которой служат нули или единицы с положительными знаками, соответствует началу линии (обозначает направление потока); Mоб – матрица, содержащая в качестве своих элементов нули или единицы с отрицательными знаками, соответствует концу линии.
Матрица смежности ориентированного графа С (n´n) определяется как матрица [C]ij=1, если поток направлен от узла i к узлу j, и может быть вычислена как
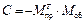 . (2)
. (2)
Матрица Рпр может быть вычислена как
 , (3)
, (3)
где diag(PВ) – диагональная матрица потоков мощностей ветвей.
Матрица суммарных мощностей в узлах РУ может быть определена как сумма узловых оттоков или притоков:
РУ=РН+Рпр×1 или РУ=РГ+Рпр×1, (4)
где 1 – единичная матрица n´1, состоящая из единиц, число строк которой равно количеству всех узлов рассматриваемой сети.
Подставляя (3) в (4), после преобразований можно получить
 (5)
(5)
 (6)
(6)
предполагая, что узлы без узловых потоков, то есть те, для которых Pi=0, были удалены из ориентированного графа так, чтобы (diagP)-1 существовала. Здесь I – единичная матрица n´n, состоящая из единиц в главной диагонали.
Матрицы Aпр и Aоб прослеживания путей вдоль и против потоков равны
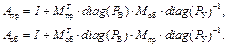 (7)
(7)
Матрицы Aпр и Aоб могут быть сформированы непосредственно из потоков ветвей без исполь- зования матричных преобразований, показанных в (7).
Уравнения (5) и (6) позволяют проследить, как потоки мощности протекают в сети от отдельных генераторов или нагрузок:
 или
или  . (8)
. (8)
Доля узлового потока Pi от местной генерации PГi равна PГi/Pi. Следовательно, используя первое уравнение (8), локальную генерацию можно выразить как линейную комбинацию компонентов, доставленных отдельным нагрузкам:
 . (9)
. (9)
Моделирование задачи адресности
Для моделирования задачи адресности разработаны методика и алгоритм, реализованные в виде MATLAB-программы, работоспособность которой проверена на различных тестовых схемах IEEE.
Алгоритм адресного распределения потоков активной мощности включает семь этапов.
1. Составление схемы замещения электроэнергии.
2. Расчет установившегося режима ЭС.
3. Информация об узлах (генерация, нагрузка) и ветвях (нумерация и потоки мощности).
4. Формирование матриц узловых инъекций мощности, потоков мощности.
5. Формирование матриц инциденций.
6. Расчет коэффициентов адресности.
7. Определение вкладов генерации в потребление.
В отличие от адресного распределения потоков активной мощности моделирование адресности передачи реактивной мощности имеет следующие особенности:
- необходимость учета емкостных проводимостей ветвей на землю;
- необходимость учета индуктивных проводимостей трансформаторов;
- увеличение числа узлов по сравнению с числом генераторов в схеме сети;
- увеличение числа нагрузочных узлов по сравнению с нагрузочными узлами.
Для учета особенностей адресности передачи реактивной мощности были разработаны дополнительные алгоритмы формирования фиктивных источников реактивной мощности, стоков реактивной мощности, фиктивных ветвей.
Для исследования адресной передачи активных мощностей были использованы 6-узловая тестовая схема IEEE, 8-узловая и 26-узловая эквивалентные схемы Азербайджанской ЭЭС.
Результаты моделирования

 На рисунке 2 приведена 6-узловая тестовая схема IEEE. Данные по узлам и ветвям, а также результаты расчета установившегося режима тестовой схемы приведены в таблицах 1 и 2.
На рисунке 2 приведена 6-узловая тестовая схема IEEE. Данные по узлам и ветвям, а также результаты расчета установившегося режима тестовой схемы приведены в таблицах 1 и 2.
На рисунке 3 приведены результаты расчета адресности и орграф 6-узловой схемы, полученный по разработанной программе.
Таблица 1
Данные по узлам тестовой 6-узловой схемы
Table 1
Data for a 6bus test scheme
|
Номер
|
Напряжение, о.е.
|
Рген, МВт
|
Qген, МВАр
|
Pнаг, МВт
|
Qнаг, МВАр
|
|
1
|
1.050
|
100
|
33.84
|
0
|
0
|
|
2
|
1.050
|
50.00
|
59.16
|
0
|
0
|
|
3
|
1.070
|
60.00
|
83.76
|
0
|
0
|
|
4
|
1.007
|
0
|
0
|
70.00
|
70.00
|
|
5
|
1.007
|
0
|
0
|
70.00
|
70.00
|
|
6
|
1.018
|
0
|
0
|
70.00
|
70.00
|
Таблица 2
Данные по ветвям тестовой 6-узловой схемы
Table 2
Data on the branches of a 6-noded test scheme
|
Номер
|
От узла
|
К узлу
|
От узла P(MW)
|
От узла Q(MVAr)
|
К узлу P(MW)
|
К узлу Q(MVAr)
|
|
1
|
1
|
2
|
25.96
|
-1.59
|
-25.96
|
-1.59
|
|
2
|
1
|
4
|
41.20
|
22.03
|
-41.20
|
-22.12
|
|
3
|
1
|
5
|
32.83
|
13.40
|
-32.83
|
-16.05
|
|
4
|
2
|
3
|
2.23
|
-11.70
|
-2.23
|
5.13
|
|
5
|
2
|
4
|
32.67
|
44.67
|
-32.67
|
-43.91
|
|
6
|
2
|
5
|
16.27
|
13.34
|
-16.27
|
-16.20
|
Результаты расчетов адресности активной мощности тестовой 6-узловой схемы по разработанной в среде MATLAB программе приведены в табли- це 3.
Таблица 3 Результаты расчетов адресности Table 3 Adressness calculation results
| |
Станция |
| Узел |
|
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
100 |
0 |
0 |
0 |
0 |
0 |
| 2 |
25.96 |
50 |
0 |
0 |
0 |
0 |
| 3 |
0.76212 |
1.4679 |
60 |
0 |
0 |
0 |
| 4 |
52.365 |
21.505 |
|
0 |
0 |
0 |
| 5 |
41.35 |
12.242 |
16.468 |
0 |
0 |
0 |
| 6 |
9.0604 |
17.393 |
43.537 |
0 |
0 |
0 |
| |
Узел |
| Узел |
|
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
100 |
0 |
0 |
0 |
0 |
0 |
| 2 |
25.96 |
75.96 |
0 |
0 |
0 |
0 |
| 3 |
0.76212 |
2.23 |
62.23 |
0 |
0 |
0 |
| 4 |
52.365 |
32.67 |
0 |
73.87 |
0 |
0 |
| 5 |
41.35 |
18.598 |
17.08 |
3.88 |
70.06 |
0 |
| 6 |
9.0604 |
26.424 |
45.155 |
0.0033229 |
0.06 |
69.99 |
| |
Станция |
| Нагрузка |
|
1 |
2 |
3 |
4 |
5 |
6 |
| 1 |
0 |
0 |
0 |
0 |
0 |
0 |
| 2 |
0 |
0 |
0 |
0 |
0 |
0 |
| 3 |
0 |
0 |
0 |
0 |
0 |
0 |
| 4 |
49.622 |
20.378 |
0 |
0 |
0 |
0 |
| 5 |
41.315 |
12.232 |
16.454 |
0 |
0 |
0 |
| 6 |
9.0617 |
17.396 |
43.543 |
0 |
0 |
0 |
Адресное распределение потерь между участниками рынка электроэнергии
Оценка потерь в электрических сетях различного класса напряжения и от транзита мощности, адресное разнесение потерь между продавцами и покупателями, нормирование потерь и т.д. являются приоритетными задачами [5, 7–10].
Для обоснования взаиморасчетов между получателями электроэнергии и владельцами транзитных сетей необходимо определить общий объем транзитных потерь в сети и распределить его между участниками энергообмена.
Таким образом, при распределении потерь активной мощности между участниками рынка электроэнергии возникают вопросы о доле участия электрических станций и потребителей электрической сети. Эти задачи возникают как на стадии заключения договоров, так и при оперативном планировании и на оптовом рынке электроэнергии и мощности.
В мировой практике реализации конкурентных отношений в электроэнергетике пока не существует единого подхода к этому вопросу.
Суть пропорционального метода состоит в том, что суммарные потери между нагрузками и генераторами делятся поровну. Недостатками данного метода являются игнорирование сети и несправедливое распределение ответственности за потери между генераторами, далекими от центра нагрузок, и генераторами, расположенными в центре нагрузок.
Маргинальный метод заключается в использовании для разделения потерь коэффициентов чувствительности суммарных потерь к изменению генераций и нагрузок в узлах. Недостатком маргинального метода является то, что он не учитывает базисный узел, в нем велик дисбаланс между потерями, отнесенными к генераторным и нагрузочным узлам.
К числу специфических особенностей распределения потерь Zy-узловым методом относятся отрицательные доли потерь мощности. Существуют специальные приемы для исключения отрицательных потерь.
В [6] рассматривается метод определения коэффициентов адресности, основанный на поиске путей на ориентированном графе и позволяющий за число циклов, равное числу генераторных узлов, определить долю активной или реактивной мощности, текущей от каждого генераторного узла по ветвям схемы сети и в нагрузочные узлы.
Моделирование распределения потерь мощности
Матрица узловых сопротивлений Zy является обобщенным параметром электрической сети. Обобщенные параметры находятся из решения системы уравнений, описывающей установившийся режим электрической сети в целом. Эти параметры могут быть получены на основе матричного и топологического методов [5].
Как известно, задача расчета установившегося режима заключается в определении значений узловых напряжений для заданных параметров электрической сети и значений узловых мощностей.
Для разделения потерь может быть использована матрица узловых сопротивлений:
 ,
,
 .
.
В целях моделирования распределения потерь Zy узловым методом разработан алгоритм, реализованный в виде программы, который опробован на различных тестовых и реальных электроэнергетических системах для локализации потерь при передаче. Алгоритм моделирования распределения потерь Zy узловым методом состоит из следующих этапов [10]:
- ввод информации;
- обращение Zy =(Yy)-1-матрицы;
- решение системы линейных уравнений;
- вычисление потерь мощности, относимых в узлы.
 Особенность методов матрицы Zy состоит в том, что надо получить, запомнить и применить в итерационных расчетах заполненную матрицу Zy. В связи с прямым решением уравнений сети напря-жение каждого узла связано с токами всех узлов, что обусловливает быструю и надежную сходимость по сравнению с итеративными методами матрицы Yy. Напряжения узлов пересчитываются последовательными приближениями. Zy-матрица определяется в явном виде. В разработанной программе Z-матрица используется как для решения уравнений установившихся режимов, так и для расчета узловых потерь (рис. 4).
Особенность методов матрицы Zy состоит в том, что надо получить, запомнить и применить в итерационных расчетах заполненную матрицу Zy. В связи с прямым решением уравнений сети напря-жение каждого узла связано с токами всех узлов, что обусловливает быструю и надежную сходимость по сравнению с итеративными методами матрицы Yy. Напряжения узлов пересчитываются последовательными приближениями. Zy-матрица определяется в явном виде. В разработанной программе Z-матрица используется как для решения уравнений установившихся режимов, так и для расчета узловых потерь (рис. 4).
 Для проверки разработанного программного обеспечения были использованы тестовые схемы IEEE и эквивалентные 8- и 26-узловые схемы ЭЭС Азербайджана (рис. 5).
Для проверки разработанного программного обеспечения были использованы тестовые схемы IEEE и эквивалентные 8- и 26-узловые схемы ЭЭС Азербайджана (рис. 5).
Проведены расчеты для эквивалентной 8-узловой схемы ЭЭС Азербайджана. Результаты этих расчетов по разработанной программе приведены в таблице 4.
Таблица 4
Потери мощности, отнесенные в узлы Zy-узловым методом
Table 4
Power losses that are distributed into nodes by Zybus method
|
Номер узла
|
Потери мощности, МВт
|
|
2
|
-0,2120
|
|
3
|
44,6629
|
|
4
|
0,0225
|
|
5
|
15,6515
|
|
6
|
4,7038
|
|
7
|
–5,7621
|
|
8
|
7.3527
|
Суммарные потери мощности в ЭЭС составили 66.4192 МВт.
Таким образом, в нагрузочных узлах 3, 5, 6 и 8 имеются наибольшие доли потерь.
Разделение потерь мощности маргинальным методом
Маргинальные коэффициенты могут быть получены либо численным методом, либо на основе прямого вычисления частных производных. В численном методе с помощью программы расчета установившегося режима определяется изменение суммарных потерь при изменении нагрузки или генерации в узле на небольшую величину:
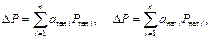
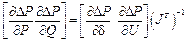 .
.
Разработана программа распределения потерь активной мощности по частным производным потерь от активных мощностей. В таблице 5 приведены результаты распределения потерь активной мощности между генераторными и нагрузочными узлами для прямого определения частных производных от потерь на примере тестовой 6-узловой схемы IEEE.
Таблица 5
Распределение потерь активной мощности между генераторными и нагрузочными узлами
Table 5
Active power losses distribution between power generation buses and PQ buses
|
Номер узла
|
Значение частного производного потерь
|
Узловая мощность, МВт
|
Потеря мощности, вычисленная по маргинальным коэффициентам
|
Скорректированный маргинальный коэффициент потерь
|
Потеря, вычисленная по нормали-зованным коэффициентам
|
|
2
|
0,0451
|
50,0
|
2,2530
|
-0,03463
|
-1,7314
|
|
3
|
0,0542
|
60,0
|
3,2491
|
-0,04161
|
-2,4968
|
|
4
|
0,0671
|
70,0
|
-4,6997
|
-0,05159
|
3,6116
|
|
5
|
0,0804
|
70,0
|
-5,6267
|
-0,06177
|
4,3239
|
|
6
|
0,0774
|
70,0
|
-5,4181
|
-0,05948
|
4,1636
|
| |
|
|
ΔP’Σ= -10,2424
|
|
ΔPΣ= 7,8709
|
Производные от потерь (табл. 5) показывают, что генераторные узлы 2 и 3 получают компенсацию за потери. Наибольшее участие в потерях принимает 5-й узел. Участие в потерях нагрузочного узла 4 минимально.
На основании изложенного сделаем следующие выводы. Децентрализация процесса производства, передачи и распределения электроэнергии в электроэнергетике привела к необходимости адресного разделения потоков мощности и энергии между участниками рынка электроэнергии.
В работе проведен анализ методов адресности потоков и потерь активных мощностей.
Для моделирования задачи адресности разработан алгоритм, реализованный в виде MATLAB-программы. Кроме того, проведена оценка ад- ресного разделения потоков и потерь активной мощности на тестовых схемах IEEE и Азербайджанской ЭЭС с использованием разработанного программного обеспечения.
Результаты моделирования адресного разделения потоков мощности и энергии позволяют определить долю участия каждой станции в снабжении конкретной нагрузки и узла.
Литература
1. Bialek J. Tracing the flow of electricity. IEEE Proc. Generation, Transmission and Distribution, 1996, vol. 143, pp. 313–320.
2. Kirschen D., Allan R., and Strba G. Contributions of individual generators to loads and flows. IEEE Trans. Power Systems, 1997, 12, February pp. 52–60.
3. Bialek J.W., Kattuman, P.A. Proportional sharing assumption in tracing methodology, Generation, Transmission and Distribution. IEEE Proc., 2004, vol. 151, iss. 4, pp. 526–532.
4. Conejo J.J., Arroyo M., Alguacil N. and Guijarro A.L. Transmission Loss Allocation: A Comparison of Different Practical Algorithms. IEEE Trans. Power Systems, 2002, vol. 17, no. 3, pp. 571–576.
5. Conejo A.J., Galiana F.D., Kockar I. Z-bus loss allocation. IEEE Trans, pp. 105–110.
6. Гамм А.З., Голуб И.И. Адресность передачи активных и реактивных мощностей в электроэнергетической системе // Электричество. 2003. № 3. С. 16–19.
7. Бартоломей П.И., Паниковская Т.Ю., Тихонов С.А. Анализ и разработка алгоритмов оценки ответственности субъектов рынка за потери электроэнергии // Энергосистема: управление, конкуренция, образование: сб. докл. III междунар. науч.-практич. конф. Екатеринбург. 2008. Т. 1. С. 623–627.
8. Баламетов А.Б., Халилов Э.Д. О прослеживании путей передачи мощностей в энергосистемах // Проблемы энергетики. 2011. № 4. С. 10–17.
9. Баламетов А.Б., Халилов Э.Д. О распределении потерь Z-узловым методом // Проблемы энергетики. 2011. № 2. С. 30–38.
10. Баламетов А.Б., Халилов Э.Д. Методы прогнозирования потерь мощности электроэнергетических систем для анализа и управления // Электричество. 2013. № 7. С. 19–29.

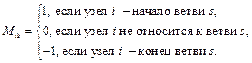
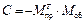 . (2)
. (2) , (3)
, (3) (5)
(5) (6)
(6)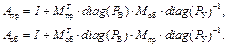 (7)
(7) или
или  . (8)
. (8) . (9)
. (9)

 ,
, .
.

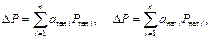
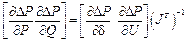 .
.