Journal influence
Bookmark
Next issue
Algorithmic software of software maintenance complex controlling the reliability level of flight facilities
Abstract:Improvement of technical means complexes is related to the need for research on extending the life of equipment while reducing operational costs. One of the ways of improving qualitative indicators of a technical condition (TC) of such complexes throughout their life cycle while reducing operational costs is the transition to technical service (TS) with pe-riodical inspection. Nowadays when using automated control systems (management information systems), maintenance methods with periodic monitoring that consider the actual condition of the equipment are becoming more and more popular. It should be noted that none of the methods is implemented without the prevention; each of them has its specificity when determining the timing and amount of preventive maintenance. To solve of the problem of determining rational frequency using statistical projections successfully, the paper proposes algorithmic support for software maintenance complex controlling the level of reliability of flight facilities. In this case, the developers of an algorithm took into account the volume and frequency of maintenance. The developed algorithm is implemented as a software complex, which allows determining optimal periods of maintenance. The algorithm efficiency is verified based on functioning of the automated workplace of a near zone head to control the engineering status of radio facilities. According to the engineering status, the software package determines the optimal maintenance periods for technical means complexes.
Аннотация:Совершенствование комплексов технических средств связано с необходимостью проведения исследований по продлению ресурса техники при снижении расходов на эксплуатацию. Одним из путей повышения качественных показателей технического состояния таких комплексов на протяжении их жизненного цикла при одновременном снижении расходов на эксплуатацию является переход на техническое обслуживание с периодическим контролем. При эксплуатации объектов АСУ все большее применение находят методы технического обслуживания с периодическим контролем, учитывающие фактическое состояние техники. При этом необходимо отметить, что ни один из методов технического обслуживания не реализуется без проведения профилактики, и каждый из них имеет свою специфику при определении сроков и объемов профилактических работ. В работе предложено алгоритмическое обеспечение программного комплекса технического обслуживания с контролем уровня надежности средств обеспечения полетов. При разработке алгоритма учитывались объем и периодичность технического обслуживания. Разработанный алгоритм реализован в виде программного комплекса, позволяющего определить оптимальные периоды технического обслуживания. Работоспособность алгоритма проверена на основе функционирования АРМ руководителя ближней зоны для контроля технического состояния средств радиосвязи. Программный комплекс позволяет определить по техническому состоянию оптимальные периоды технического обслуживания комплексов технических средств.
| Authors: Dopira R.V. (rvdopira@yandex.ru) - NPO RusBITex (Professor, Head of Department), Tver, Russia, Ph.D, V.A. Dikarev (dikva@mail.ru) - Institute of Mathematics, Informatics and Natural Sciences, Moscow City Pedagogical University (Professor, Head of Chair), Moscow, Russia, Ph.D, Potapov A.N. (potapov_il@mail.ru) - Military scholastic-scientific centre of the Air forces "Air forces academy named by prof. N.E. Zhukovsky and Yu.A. Gagarin", Voronezh, Russia, Ph.D, E.E. Bueshev (rvdopira@yandex.ru ) - Military Scholastic-Scientific Centre of the Air Forces "Zhukovsky and Gagarin Air Forces Academy" (Adjunct ), Voronezsh, Russia, I.A. Yuriev (rvdopira@yandex.ru ) - Central Research Radiotechnical Institute named after academician A.I. Berg (Deputy Head), Moscow, Russia, Ph.D | |
| Keywords: software package, technical means, control, level of reliability, maintenance service, algorithmic support |
|
| Page views: 7335 |
PDF version article Full issue in PDF (19.46Mb) |
Для успешного решения задачи определения рациональной периодичности проведения технического обслуживания (ТО) с использованием методов статистического прогнозирования предлагается алгоритм прогнозирования ТО технических средств (ТС) обеспечения полетов с контролем уровня надежности [1]. В отличие от известных постановок задачи при использовании предлагаемой системы ТО учитывалось требование периодичности ТО, а также то, что объем работ очередного ТО включает в себя все виды предшествующих. В качестве критерия эффективности проведения ТО с контролем уровня надежности рассматривается максимальная вероятность безотказной работы системы на заданном отрезке времени при ограничениях на суммарные затраты, связанные с проведением профилактических работ [2]. При этом предполагается, что отказ любого изделия приводит к отказу системы в целом. Таким образом, максимальная вероятность безотказной работы является гарантированным уров- нем надежности. Для большинства сложных объек- тов, содержащих большое количество различных элементов, используется экспоненциальный закон распределения вероятности безотказной рабо- ты [3]. Исходя из того, что отказ любого элемента приводит к отказу системы, математическую постановку задачи сформулируем следующим образом. Пусть функциональная система состоит из m элементов. Элемент j (j Î {1, 2, …, m}) имеет интенсивность отказов lj. При ТО с контролем уровня надежности вида i (i Î {1, 2, …, n}) контролю подвергается множество элементов Si (Si Ì Si+1, Sn, n = {1, 2, …, m}) c соответствующими затратами ri. Задано время эксплуатации Т. Требуется определить оптимальный набор периодов ТО элементов E* {t i* , i = 1, …, n} Ì E, при котором суммарные затраты R(E) не превышают допустимую величину R0 и выполняется условие
где t Î [0, T], P(E, t) – вероятность безотказной работы системы. С учетом повторяемости процесса изменения P(E, t) с периодом tn определялось Р(Е) как вероятность безотказной работы системы в момент времени, предшествующий очередной проверке n: P(E) = где Аi = Si /Si–1 – множество элементов системы, которые не проверялись к моменту ti ( Суммарные затраты R(E) с учетом того, что ТО вида i на интервале [0, ti+1] проводится ti+1/tI – 1 раз, определялись следующим образом:
Задача выбора оптимального набора периодов ТО сводится к отысканию набора Е* = {ti, i = 1, 2, …, n} интервалов времени между проверками ti, при котором
Данная задача решалась методом динамического программирования. Для этого вводились переменные xi (xi = ti+1/ti 1, 2, …, xn = T/tn = 1, 2, …) и t выражалось через xi: Тогда ai = T
Требуется найти набор Х* = (хi*, i = 1, 2, …, n), соответствующий оптимальной периодичности проверок, при котором выполняется условие (4). С помощью рекуррентного уравнения, полученного путем применения принципа оптимальности Беллмана, на каждом этапе вычислений определялась функция fi(Ri) – min суммарной интенсивности отказов при проведении проверок, решения о проведении которых были приняты на этапах 1, 2, …, i – 1 при заданном состоянии затрат R:
При последовательном вычислении fi(Ri) (i = 1, 2, …, n) на шаге n определяется fin(R0) = –ln P* (X*). Для решения уравнения (8) на каждом шаге i предварительно перебором находится множество значений вспомогательной функции:
0 £ Фi,b £ R0, a = 1, li-1, xi =1, 2, … Тогда {fi(Ri)} Í {Li(Ri)} определим в виде мажорирующей последовательности, потребовав для каждого члена a{fi(Ri)} выполнение условия fi,a =
Программная реализация алгоритма ТО с контролем уровня надежности комплексов ТС обеспечения полетов Разработанный алгоритм ТО с контролем уровня надежности ТС обеспечения полетов, входящих в состав комплекса средств руководства полетами (КСРП-А), предназначенного для решения задач по автоматическому сбору и обработке информации о воздушной обстановке в аэродромной зоне и непосредственного управления полетами и посадкой воздушных судов с командно-диспетчерского пункта аэродрома, реализован в виде программного комплекса, позволяющего определить оптимальные периоды ТО [6, 7]. Работоспособность алгоритма была проверена на основе функционирования АРМ руководителя ближней зоны для контроля ТС радиосвязи [8]. С этой целью определена периодичность прове- дения четырех проверок шести элементов – интенсивность отказов элементов λj = ={2×10-7, 8×10-7, 1×10-7, 0,4×10-7, 0,8×10-7, 3×10-7}; – время эксплуатации элементов, входящих в состав КСРП-А, Т = 8640 ч; – затраты на проведение профилактических работ R0 = 15 ч. Из формул (2) и (5) определяются Ai и ai. Например: A3 = S3 \ S2 = {1, 2, 3, 4, 5} \ {1, 2, 3} = {4, 5}. Значения количества элементов – Si, затрат на проведение профилактических работ – ri (i = Таблица 1 Значения количества элементов, затрат на проведение профилактических работ, множество элементов системы и интенсивности отказов Table 1 The number of elements, the cost of maintenance works, a set of system elements and failure rate
Таблица 2 Значения элементов Table 2 The values of elements
Например, при х2 = 2 и 1,a = 1,3: L2,11 = (f1,3 = 2,88×10-2) (x2 = 2) + (a2 = 0,864×10-2) + + (a2 = 0,864×10-2) / (x2 =2) = 1,872×10-2, F2,11 = (R1,3 = 4)×(x2 = 2) + ((x2 = 2) – 1)×(r2 = 3) = 11. Из выражений (10) и (11) выделяется последовательность {f2(R2)}, члены которой отмечены номерами a в правом верхнем углу соответствующих клеток таблицы 2. Например, пусть выделены первые четыре члена {f2(R2)}. Для определения члена a = 5 предварительно определяется подмножество С2,5. Для этого, используя (11), в таблице 2 отыскиваются члены {L2(F2)} с номерами b = 4, 8, 10, 17, отвечающие условию L2,b < f2,4 = L 2,3 = 3,744×10-2, и выделяется среди них подмножество С 2,5 = {4, 13} членов, обладающих минимальным F2,b = R2,b = 6, На следующих i = 3, 4 шагах поиска проводятся аналогичные вычисления, результаты которых приведены в таблице 3. Это означает, что элементы 1 и 2 необходимо проверять с периодичностью 199 ч, а элементы 1, 2, ..., 6 с периодичностью 399 ч. При этом вероятность безотказной работы Р* = 0,964 [9]. Из таблицы 3 –ln P* = f4,10 = 3,686, Х* = {3, 1, 1, 2} и Это означает, что элементы 1, 2 необходимо проверять с периодичностью 1 440 ч, а элементы 1–6 с периодичностью 4 320 ч. При этом вероятность безотказной работы Р* = 0,964. На рисунках 1 и 2 показаны, соответственно, заданные и выходные параметры оптимизации периодичностей проверок ТС обеспечения полетов на основе программного комплекса ТО с контролем уровня надежности. Структура программного комплекса ТО с контролем уровня надежности средств обеспечения полетов Разработанный алгоритм ТО с контролем уровня надежности комплекса технических средств (КТС) обеспечения полетов реализован в виде программного комплекса, структура которого представлена на рисунке 3. Работоспособность данного алгоритма проверена на основе функционирования АРМ руководителя ближней зоны для контроля ТС средств радиосвязи. Программный комплекс ТО с контролем уровня надежности средств обеспечения полетов позволяет по техническому состоянию определить оптимальные периоды ТО КТС. Литература 1. Дикарев В.А. Обработка параметров системы информационного обеспечения авиационных комплексов радиоэлектронной борьбы // Радиотехника. 2001. № 4. С. 59–64. 2. Абу-Абед Ф.Н., Помазуев О.Н., Платонов А.Ю., Миро- нов А.М., Рюмшин А.Р. Методика определения показателей качества обнаружения радиолокационных станций // Программные продукты и системы. 2014. № 2. С. 118–124. 3. Буешев Е.Е. Техническая эксплуатация радиоэлектронных средств по состоянию // Основные направления адаптации объединенной системы ПВО государств-участников СНГ к решению задач воздушно-космической обороны: сб. матер. Междунар. воен.-науч. конф. 2016. Т. 1. С. 33–38. 4. Кирпичников А.П., Моисеев С.Н., Лебедев В.В., Сухарев В.А., Герасимов И.В., Олешко В.С., Ткаченко Д.П. Оп- тимизация методов технического обслуживания радиотехнических систем // Вестн. Казанского технологич. ун-та, 2013. № 14. С. 178–181. 5. Сысоев В.В., Крутских П.П., Свинцов А.А. Математическая модель информационного конфликта // Радиотехника. 2001. № 3. С. 77–80. 6. Лебедев В.В., Потапов А.Н. Оптимизация периодичности и объема профилактических работ при планировании и организации технического обслуживания комплексов («ОПОПР – ПОТОК»). Свид. о гос. регистр. прогр. для ЭВМ 2007610585. Российская Федерация. № 2006614190; заявл. 08.12.06; зарегистр. 06.02.07. 7. Бунин А.В., Потапов А.Н., Буешев Е.Е. Модернизированный метод формирования смешанной системы управления техническим состоянием на основе декомпозиции комплексов радиотехнических средств // Науч. вестн. МГТУ ГА. 2017. Т. 20. № 5. С. 61–74. 8. Александровская Л.Н. Современные методы обеспечения безотказности сложных технических систем. М.: Логос, 2003. 208 с. 9. Isermann R. Fault diagnosis of machines via parameter estimation and knowledge processing. Ibid. 2003, vol. 29, no. 4, pp. 815–835. 10. Gertler J. Survey of model-based failure detection and isolation in complex plants. Proc. IEEE Control Systems Magazine, 2008, vol. 21, no. 4, pp. 361–376. |
| Permanent link: http://swsys.ru/index.php?id=4465&lang=en&page=article |
Print version Full issue in PDF (19.46Mb) |
| The article was published in issue no. № 2, 2018 [ pp. 338-342 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Программное обеспечение АСУ тренажной подготовкой операторов эрготехнических радиоэлектронных средств
- Алгоритмическое и программное обеспечение символьных вычислений для логического дифференциального и интегрального исчислений
- Программный комплекс моделирования диаграммынаправленности фазированной антенной решетки и вычисления кодов фазовращателей
- Многофункциональный программный комплекс теплового проектирования электронных систем: требования к архитектуре и функциональным возможностям моделирования
- Программный комплекс обнаружения аномалий формы рельсовых путей
Back to the list of articles
 , (1)
, (1) Pi(ti) =
Pi(ti) =  , (2)
, (2) = {1, 2, …, m}) [5].
= {1, 2, …, m}) [5]. , где tn+1 = T. (3)
, где tn+1 = T. (3) . (4)
. (4)
 (5)
(5) (6)
(6)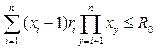 . (7)
. (7) . (8)
. (8) ,
, (9)
(9) , (10)
, (10) . (11)
. (11) , (микросхемы со средней степенью интеграции, тран- зисторы германиевые до 2мВт, конденсаторы ке- рамические, резисторы пленочные, дроссели, катушки индуктивности), входящих в состав КСРП-А в ходе проведения профилактических работ, при следующих начальных данных [9]:
, (микросхемы со средней степенью интеграции, тран- зисторы германиевые до 2мВт, конденсаторы ке- рамические, резисторы пленочные, дроссели, катушки индуктивности), входящих в состав КСРП-А в ходе проведения профилактических работ, при следующих начальных данных [9]: ), множество элементов системы – Аi, которые не проверялись к моменту ti и интенсивности отказов ai, представлены в таблице 1. Далее находятся
), множество элементов системы – Аi, которые не проверялись к моменту ti и интенсивности отказов ai, представлены в таблице 1. Далее находятся  и R1,a = (x1 –1)×r1 £ R0 (х1 = a = 1, 2, ...). Значения суммарной интенсивности отказов f1,a, затрат R1,a и переменных х1 = a записываются в верхнюю строку таблицы 2. Для каждого возможного x2 и 1,a вычисляется L2,b, F2,b, X2,b = {x1, x2}, b =
и R1,a = (x1 –1)×r1 £ R0 (х1 = a = 1, 2, ...). Значения суммарной интенсивности отказов f1,a, затрат R1,a и переменных х1 = a записываются в верхнюю строку таблицы 2. Для каждого возможного x2 и 1,a вычисляется L2,b, F2,b, X2,b = {x1, x2}, b =  [10].
[10].
 Таким образом, пятым членом {f2(R2)} является член {L2,b} с номером b = 4.
Таким образом, пятым членом {f2(R2)} является член {L2,b} с номером b = 4. .
.

