Software & Systems

Введение. Решение задачи интеллектуального управления подразумевает наличие свойств адаптации и обучения в системе автоматического управления, например, подбор определенных параметров регуляторов, описывающих оптимальное поведение системы в условиях внешних и внутренних возмущений. Проверка и прогнозирование поведения системы в таких условиях осуществляются с помощью математической модели, в том числе в системе виртуальной реальности [1]. Однако поиск оптимальных решений усложняется внешними факторами, влияющими на поведение системы, например, температурой окружающей среды [2]. Существуют примеры систем, поведение которых зависит и от свойств объекта, с которым они взаимодействуют, как в случае летательного манипулятора, открывающего дверь [3]. Такие внешние факторы трудно учитывать в математической модели, и они остаются в большей мере недоопределенными. Для обучения системы автоматического управления, содержащей недоопределенные (не учитываемые в математической модели объекта управления) параметры, нужен новый подход, позволяющий получать результат без применения точной математической модели.

Обзор существующих подходов

Применение теории интеллектуального управления рассмотрим на примере физиче- ской модели робота-манипулятора. В этой модели возмущениями выступают, в частности, износ деталей, их брак или заводские люфты приводов и редукторов, трения в местах крепления осей вращения робота или дополнительная нагрузка, которой оперирует робот [4]. Данные особенности объекта управления вносят множество недоопределенных параметров, влияющих на поведение системы управления. Задачи адаптации и обучения для подобных систем могут быть решены путем подбора значений коэффициентов усиления традиционных ПИД-регуляторов в обратной связи, например, с помощью моделирования поведения манипулятора в среде Matlab Simulink [5]. Подбор оптимальных коэффициентов при этом может быть выполнен с помощью технологии интеллектуальных вычислений и генетического алгоритма (ГА) [6]. Главный недостаток данного подхода состоит в необходимости иметь математическую модель для настройки параметров системы управления.

Другой подход к управлению роботом-манипулятором состоит в применении алгоритма инверсной (обратной) кинематики [7]. Обратная кинематика позволяет работать с математическими и компьютерными моделями объектов управления, что при должной верификации с реальным объектом позволяет извлекать обучающие траектории системы с различными начальными условиями. Однако такой подход имеет и свои ограничения, в частности, не учитываются физические особенности системы, канала обратной связи, зашумленность и точность позиционирования объекта управления и др.

Принцип глобальной отрицательной  обратной связи

Задача управления объектом, как правило, подразумевает перевод объекта управления  в целевое положение в фазовом пространстве состояний. Чтобы определить силу управляющего воздействия, используют обратную связь. Обратная связь может быть и положительной, когда изменение управляющего воздействия совпадает по знаку с изменением выходного сигнала, что, как правило, приводит к экспоненциальному росту выходного сигнала, и отрицательной – в этом случае система стремится к стабильному целевому значению.

Целевые значения достигаются с помощью разных типов регуляторов. Широкое распространение получили пропорциональные (П), пропорциональные интегральные (ПИ), пропор- циональные дифференциальные (ПД) и про- порциональные интегрально-дифференциальные (ПИД) регуляторы [8]. Интегральная составляющая регулятора позволяет устранить в системе статическую ошибку, дифференциальная – улучшить динамические показатели, форсируя переходный процесс, а пропорциональная формирует точность позиционного управления.

В качестве обратной связи используются показания датчиков. В данной работе сенсорная часть была реализована средствами машинного зрения. На изображении, полученном стандартной камерой в 2D-формате, определяются отклонения текущей позиции манипулятора от целевых координат захватывающего объекта.

Описание аппаратной реализации  объекта управления

На робототехническом полигоне Лаборатории информационных технологий им. М.Г. Мещерякова Объединенного института ядерных исследований (г. Дубна) была поставлена задача разработать систему с наглядной демонстрацией управления объектом со множеством недоопределенных параметров. В качестве объекта управления выбран стационарный четырехосный робот-манипулятор. Манипулятор собран из общедоступных компонентов и имеет множество люфтов (рис. 1).

Задача манипулятора – захватить заданный объект, произвольно расположенный перед ним, при этом захват объекта осуществляется по принципу глобальной отрицательной обратной связи. Для определения положения цели и, соответственно, вычисления ошибки используется простейший детектор на основе веб-камеры и методов машинного зрения.

Управление манипулятором осуществляется с помощью одноплатного компьютера Raspberry PI4, который взаимодействует с контроллером манипулятора по COM-порту. Манипулятор входит в состав экспериментального полигона и управляется по локальной сети с помощью REST API [9]. Видеосигнал поступает с web-камеры, подключенной непосредственно к одноплатному компьютеру. Сонар подключен к контроллеру манипулятора. Анализ кадров, полученных с USB-камеры, выполняется полностью на одноплатном компьютере. Для этих целей был разработан простейший алгоритм обнаружения, реализованный  с использованием библиотеки OpenCV. Алгоритм обнаружения представляет собой следующую последовательность шагов:

– задание диапазонов допустимых значений цвета по трем каналам;

– получение изображения с камеры;

– предобработка изображения: перевод его в цветовое пространство HSV и размытие фильтром Гаусса с радиусом 11;

– отбрасывание пикселей, значения которых не подходят под заданные допустимые значения цветового канала;

– выделение контуров на основе оставшихся пикселей;

– выбор контура с максимальной площадью;

– если площадь выбранного контура больше 100 (защита от ложного срабатывания), то возврат прямоугольника, обрамляющего контур,  в противном случае возврат прямоугольника нулевого размера.

Как уже упоминалось, рассматриваемый манипулятор имеет четыре сервопривода: первый расположен в основании робота, последний в захвате. Минимальные и максимальные значения заложены в виде констант в программе контроллера, а стартовые хранятся  в энергонезависимой памяти.

Процесс захвата объекта происходит итеративно, с помощью машинного зрения манипулятор определяет положение объекта и перемещается в его сторону. Процесс останавливается на основании показаний сонара, когда информация о размере и положении искомого объекта подтверждает, что он находится в зоне работы захвата.

Этапы решения задачи

Вычисление смещения манипулятора. Для вычисления обновленных углов приводов манипулятора необходимо рассчитать, насколь- ко нужно переместить захват манипулятора с камерой, чтобы объект оказался в рабочей зоне захвата. Есть несколько путей для достижения этой цели.

Один из них – использовать знание геометрии манипулятора, измерить положение камеры, исправить дисторсию объектива камеры и вычислить коэффициенты пересчета координат из детектора в физическое положение объекта относительно камеры. Однако, во-первых, это крайне трудоемкий процесс, поскольку измерения и калибровка требуют больших временных затрат и уникальны для конкретного устройства. Во-вторых, качество деталей манипулятора очень низкое, учесть все неточности печати и сборки крайне затруднительно. В-третьих, поворот сервоприводов осуществляется неточно с люфтом местами до трех градусов  и с шагом порядка одного градуса, что значительно сказывается на точности наведения.

Другой путь заключается в использовании итеративного процесса корректировки положения осей манипулятора с маленьким шагом таким образом, чтобы система постепенно сходилась к положению, когда объект находится в зоне работы захвата. Для этого нужно сменить стандартную систему координат изображения, при которой центр координат находится  в верхнем левом углу, на систему координат  с центром, совпадающим с целевым положением объекта в кадре. После данного преобразования координат положение объекта можно представить как ошибку, которую требуется минимизировать. При успешном решении этой задачи камера будет наведена точно на объект. Но для захвата нужно не просто повернуться  в сторону объекта, но и приблизиться к нему.  В качестве характеристики расстояния до объекта была использована разница между целевой шириной объекта в кадре и шириной объекта из результатов работы детектора.

Таким образом, была получена некая характеристика, которую также нужно минимизировать.

За движения робота по направлению к объекту отвечают три сервопривода, при этом на ошибку положения по осям Y и Z влияют сразу два из них. В первом приближении задача вычисления обновленного положения на каждом шаге может быть решена методом подбора коэффициентов для системы уравнений:

p1 = p1 + w11errx + w12erry + w13errz,

p2 = p2 + w21errx + w22erry + w23errz,

p3 = p3 + w31errx + w32erry + w33errz,

где pi  – значение угла i-го сервопривода; errx, erry  – ошибки положения центра объекта; errz  – характеристика расстояния до объекта; wij  – веса влияния соответствующей ошибки на положение сервопривода.

Первый привод выполняет поворот манипулятора относительно основания и не может влиять на величины erry и errz. По этой причине w12 и w13 можно приравнять к нулю и опустить, как и пренебречь членами w21 и w31.

Поскольку шаг работы сервоприводов довольно большой, а конструкция манипулятора имеет множество люфтов, такой подход работает только в случае небольших значений весов, а это значит, что робот будет достигать цели достаточно медленно. Исправить это и сгладить формы движения можно с помощью ПИД-регулятора. Чтобы не перегружать уравнения дополнительными коэффициентами, можно использовать ПД-регулятор, который показал свою эффективность при стабилизации подобных процессов [10, 11].

Эмпирически было установлено, что применение ПД-регуляторов вместо пяти весовых коэффициентов приводит к непредсказуемым резким движениям манипулятора при приближении к искомому объекту. Предположительно, при некоторых положениях объекта два ПД-регулятора входят в резонанс, что приводит к экстремально большому шагу сервоприводов, и робот теряет объект из поля зрения телекамеры.

Чтобы ПД-регуляторы не оказывали нежелательного воздействия друг на друга, их количество должно соответствовать количеству управляемых сервоприводов. В представленной модели ошибки erry и errz имеют очевидную связь при влиянии на сервоприводы 2 и 3. Влияние данных ошибок на каждый привод необязательно равнозначное, поэтому справедливо будет ввести весовые коэффициенты влияния каждой ошибки на соответствующий привод. Пусть нумерация приводов начинается с 1, при этом первый привод – карусель робота. Тогда для всех приводов можно будет вычислить ошибки по следующим уравнениям:

err1 = errx,

err2 = aerry + berrz,

err3 = cerry + derrz,

или

err1 = errx,

err2 = a(erry + b/a errz),

err3 = c(erry + d/c errz),

где a, b, c и d – пропорциональные коэффициенты линейной зависимости ошибок erry и errz.

Формула ПД-регулятора:

pi = pi + Pi + Di,

где i  – номер сервопривода; pi – значение угла сервопривода; Pi и Di – пропорциональная  и дифференциальная части ПД-регулятора сервопривода.

Вычисление пропорциональной части ПД-регулятора первого сервопривода осуществляется по формуле

P1 = kp1err1 = kp1errx,

где kp1  – пропорциональный коэффициент для ПД-регулятора первого сервопривода.

Пропорциональная часть второго и третьего приводов вычисляется аналогично:

P2 = kp2err2 = kp2a(erry + b/a errz) = kp2'(erry +  + a'errz),

P3 = kp3err3 = kp3c(erry + d/c errz) = kp3'(erry +  + c'errz),

где kp2' = kp2 a; a' = b/a; kp3' = kp3 c; c' = d/c.

Дифференциальная составляющая для первого сервопривода:

D1 = kd1(err1 – err1(t-1)) = kd1(errx – errx(t-1)),

где err1 – ошибка положения первого сервопривода; err1(t-1) – ошибка положения сервопривода на предыдущем шаге; kd1 – дифференциальный коэффициент для регулятора первого сервопривода.

Дифференциальная часть второго и третьего сервоприводов включает две компоненты ошибки. Для второго сервопривода это будет выглядеть так:

D2 = kd2(err1 – err1(t-1)) = kd2(a(erry + b/a errz) –  – a(erry(t-1) + b/a errz (t-1))).

После раскрытия скобок:

D2 = kd2a(erry – erry(t-1) + b/a(errz – errz(t-1))) =  = kd2'(erry – erry(t-1) + a'(errz – errz (t-1))),

где kd2' = kd2 a; a' = b/a.

Для дифференциальной части третьего привода все аналогично и после повторения операций принимает вид

D3 = kd3'(erry – erry(t-1) + c'(errz – errz(t-1)),

где kd3' = kd3 c; c' = d/c.

Таким образом, решение задачи управления сводится к подбору восьми коэффициентов: kp1, pd1 – для первого привода, kp2', kd2' и a' – для второго привода, kp3', kd3' и c' – для третьего привода.

Применение ГА для оптимизации подбора параметров управления. Первоначально задача подбора параметров была решена путем эмпирического перебора. Удалось подобрать такие значения, при которых манипулятор стал стабильно достигать цели, но для этого ему требовалось большое число шагов (порядка 40). В качестве альтернативного способа подбора оптимальных значений были рассмотрены эволюционные алгоритмы, основное место среди которых занимает ГА [6, 12].

Существует множество вариантов реализации ГА, и большинство из них оперируют бинарными генами. В рассматриваемой задаче параметры представляют собой числа с плавающей точкой, поэтому требовалось найти метод кодирования набора чисел с плавающей точкой в бинарные хромосомы. В качестве языка программирования использован Python3, стандартные методы битового кодирования в котором привязаны к количеству байт на число (1, 2, 4 или 8). Алгоритм позволяет производить поиск оптимальных значений в заданном интервале, прямое кодирование чисел в биты приведет как минимум к тому, что не все эти биты будут задействованы.

С другой стороны, можно представить интервал значений параметра как линейку, на  которой будет столько делений, сколько мы сможем закодировать в выбранное число байт. Таким образом, было принято решение о преобразовании всех дробных чисел в целые, описывающие номер деления на этой виртуальной линейке:

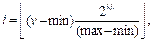
где i – целое число, характеризующее значение v в заданном интервале [min, max]; b – число байт в i.

Обратное преобразование:

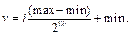
После данного преобразования получаем хромосому длиной, равной произведению числа параметров на b. Генерация случайной особи представляет собой генерацию нужного количества случайных байт. Рекомендуется, чтобы мутация каждого гена производилась  с вероятностью 1/8b. Отбор сделали элитарным, чтобы не терять хорошие решения.

Сам алгоритм представляет собой последовательность перечисленных далее шагов.

1. Случайным образом генерируется нулевая популяция заданного размера.

2. Выполняется оценка каждой особи популяции.

3. Создается новая популяция, и в нее переносятся N лучших особей из предыдущей.

4. Случайным образом выбираются две разные особи из предыдущей популяции. Выбор осуществляется с помощью модуля случайного значения, полученного из нормального распределения, с математическим ожиданием в 0  и среднеквадратичным отклонением в 30 %  от размера популяции.

5. С вероятностью P1 выполняется двухточечный кроссинговер.

6. Выбранные ранее или полученные после скрещивания особи добавляются в новую популяцию.

7. Повторяются шаги 4–6 до тех пор, пока размер новой популяции не будет равен заданному размеру.

8. Для всех особей со 2-й с вероятностью P2 применяется оператор мутации.

9. Выполняется оценка всех особей.

10. Повторяются шаги 3–9 столько раз, сколько поколений было задано при запуске.

11. Выбирается лучшая особь в качестве результата.

Подбор оптимальных параметров управления. В качестве цели были выставлены значения, полученные из машинного зрения (рис. 2).

Ошибки вычисляются следующим образом:

errz = 0.5 – width,

errx = 0.44 – x,

erry = 0.82 – y.

Для оценки качества коэффициентов в REST API манипулятора были добавлены новые Action и Service [9] с одинаковым именем checkcoeffs. Action принимает в качестве параметров восемь значений коэффициентов. Работа Action повторяет работу Action захвата объекта до момента захвата, то есть робот итеративно движется к объекту, но не зажимает его захватом, а возвращается в стартовое положение. При вычислении оценки была применена парадигма минимизации ошибки: чем меньше значение оценки, тем лучше. Для реализации этого условия во время работы программы проверки коэффициентов идет суммирование ошибки положения объекта по результатам машинного зрения. Оценка вычисляется по формуле S = Ʃi=2di((errzi) + (erryi) + (errxi)), где di – число шагов с успешной детекцией объекта на i-м шаге процедуры. Первый шаг из оценки исключен, так как ошибка первого шага зависит от начального положения манипулятора  и объекта и никак не зависит от проверяемых коэффициентов.

Если в какой-то момент объект выходит из поля зрения телекамеры, ошибка приравнивается к постоянному, заведомо большому значению. Объект может выйти из поля зрения телекамеры на первом же шаге, а может и через некоторое ненулевое количество шагов. Если придется выбирать из плохих решений, очевидно, что, чем больше шагов робот сделает до потери объекта из поля зрения, тем лучше. Поэтому финальное значение ошибки неудачного захвата объекта вычисляется как постоянное заведомо большое значение за вычетом числа шагов с успешно обнаруженным объектом. Также было принято решение ограничить число шагов до 100.

Проверка коэффициентов осуществляется полностью на стороне робота. Для получения значения оценки используется запрос информации из Service checkcoeffs. Ответ в поле data содержит число с плавающей точкой.

Для подбора параметров был запущен описанный выше ГА со следующими параметрами: размер популяции – 80, вероятность  мутации особи – 0.1, вероятность скрещива- ния – 0.5, элитарная часть – 10 %, число поколений – 15.

Диапазоны параметров выбраны на основе значений, подобранных эмпирически на преды- дущем этапе. В качестве размера интервала выступило удвоенное значение соответствующего параметра.

При каждом выполнении функции проверки (функции пригодности) производилась запись проверяемых коэффициентов и результата проверки для последующего анализа. Значения функции пригодности во времени представлены на рисунке 3 (важно отметить, что оценки непригодных решений (когда робот не дошел до объекта) на данном графике не отражены).

О том, что значения коэффициентов сходятся, можно судить по графикам изменения значений коэффициентов (http://www.swsys.ru/ uploaded/image/2024-3/1.jpg).

Результаты экспериментов

Поскольку функция оценки качества выбора коэффициентов зависит от множества случайных факторов, было произведено по 30 запусков для коэффициентов, подобранных вручную, и коэффициентов, полученных с помощью ГА. Результаты распределения значений представлены на рисунках 4 и 5.

С новыми коэффициентами манипулятор стал быстрее достигать объекта. Для достижения цели при использовании эмпирически подобранных коэффициентов в среднем требуется около 40 шагов, при использовании коэффициентов ГА – около 10.

Анализ результатов

Проведенные эксперименты показали, что манипулятор достигает цели значительно быстрее, количество шагов, необходимых для захвата объекта, сократилось примерно в четыре раза. Значения отклонений от цели сходятся равномернее без резких скачков в сторону увеличения. Однако следует отметить, что работа манипулятора не является идеальной: при некоторых положениях объекта заметны довольно сильные колебания манипулятора относительно цели.

Выводы

На примере четырехосного робота-манипулятора была построена система управления объектом с множеством недоопределенных параметров, работающая по принципу глобальной отрицательной обратной связи. Параметры демонстрируемой системы подбирались с применением ГА на физическом объекте в режиме реального времени и без применения математической модели объекта управления. Таким образом, была наглядно продемонстрирована возможность реализации подобных систем и применения ГА в режиме реального времени. Представленные методы технологии проектирования интеллектуальных систем могут быть перенесены и на другие объекты управления.

В данном случае применение только ГА не позволило достичь полной робастности управления объектом, так как резкие и сильные из- менения окружающей среды могут привести  к значительным колебаниям ошибок по мере приближения к цели. Создана платформа для дальнейших исследований и демонстрации возможностей алгоритмов. Следующим этапом может стать, например, применение нечетких  и квантовых нейронных сетей для выбора коэффициентов управления.

Список литературы

1.   Pascher M., Kronhardt K., Goldau F.F., Frese U., Gerken J. In time and space: Towards usable adaptive control  for assistive robotic arms. ArXiv, 2023, art. 2307.02933. URL: https://arxiv.org/pdf/2307.02933 (дата обращения: 21.03.2024).

2.   Guist S., Schneider J., Ma H., Chen L. et al. A robust open-source tendon-driven robot arm for learning control of dynamic motions. ArXiv, 2023, art. 2307.02654. URL: https://arxiv.org/pdf/2307.02654 (дата обращения: 21.03.2024).

3.   Cuniato E., Geles I., Zhang W., Andersson O., Tognon M., Siegwart R. Learning to open doors with an aerial manipulator. ArXiv, 2023, art. 2307.15581. URL: https://arxiv.org/abs/2307.15581 (дата обращения: 21.03.2024).

4.   Параев Ю.И., Колесникова С.И., Цветницкая С.А. Управление роботом-манипулятором в условиях неопределенности // Вестн. ТГУ. Управление, вычислительная техника и информатика. 2021. № 57. С. 4–12. doi: 10.17223/ 19988605/57/1.

5.   Лебедев С.К., Колганов А.Р. Модификация и настройка ПИД-регуляторов систем позиционирования промышленных манипуляторов // ЭиЭ: теория и практика: матер. III Всеросс. науч.-практич. конф. 2017. С. 1–13.

6.   Рядчиков И.В., Гусев А.А., Сеченев С.И., Никульчев Е.В. Генетический алгоритм поиска параметров  ПИД-регуляторов системы стабилизации шагающего робота // Тр. НГТУ им. Р.Е. Алексеева. 2019. № 1. С. 52–60.

7.   Santos M.C., Molina L., Carvalho E.A.N., Freire E.O., Carvalho J.G.N., Santos P.C. FABRIK-R: An extension developed based on FABRIK for robotics manipulators. IEEE Access, 2021, vol. 9, pp. 53423–53435. doi: 10.1109/ ACCESS.2021.3070693.

8.   Кузнецов Е.А., Ульянов С.В. Разработка интеллектуальной системы управления многозвенным роботом- манипулятором // Системный анализ в науке и образовании. 2022. № 3. С. 161–179. URL: http://sanse.ru/download/ 477 (дата обращения: 21.03.2024).

9.   Катулин М.С., Кузнецов Е.А., Решетников А.Г., Рябов А.Р., Семашко С.В., Ульянов С.В. Механизмы обмена информацией и передачи знаний для задач взаимодействия в среде автономных интеллектуальных робототехнических систем в нештатных ситуациях // Системный анализ в науке и образовании. 2021. № 4. С. 44–62.  URL: http://sanse.ru/download/450 (дата обращения: 21.03.2024).

10. Бухтояров И.В., Кошкина И.Н. Создание ПД регулятора для квадрокоптера // StudNet. 2020. № 10.  URL: https://stud.net.ru/sozdanie-pd-regulyatora-dlya-kvadrokoptera/ (дата обращения: 21.03.2024).

11. Кравченко П.П., Куликов Л.И., Щербинин В.В. Применение метода оптимизированных дельта-преобразований в задаче управления посадкой беспилотного летательного аппарата // Изв. РАН. Теория и системы управления. 2019. № 5. С. 130–144. doi: 10.1134/S0002338819050093.

12. Сайранов А.С., Касаткина Е.В., Нефедов Д.Г., Русяк И.Г. Применение генетических алгоритмов для управления организационными системами при возникновении нештатных ситуаций // Компьютерные исследования  и моделирование. 2019. Т. 11. № 3. С. 533–556. doi: 10.20537/2076-7633-2019-11-3-533-556.

References

1. Pascher, M., Kronhardt, K., Goldau, F.F., Frese, U., Gerken, J. (2023) ‘In time and space: Towards usable adaptive control for assistive robotic arms’, ArXiv, art. 2307.02933, available at: https://arxiv.org/pdf/2307.02933 (accessed March 21, 2024).

2. Guist, S., Schneider, J., Ma, H., Chen, L. et al. (2023) ‘A robust open-source tendon-driven robot arm for learning control of dynamic motions’, ArXiv, art. 2307.02654, available at: https://arxiv.org/pdf/2307.02654 (accessed March 21, 2024).

3. Cuniato, E., Geles, I., Zhang, W., Andersson, O., Tognon, M., Siegwart, R. (2023) ‘Learning to open doors with an aerial manipulator’, ArXiv, art. 2307.15581, available at: https://arxiv.org/abs/2307.15581 (accessed March 21, 2024).

4. Paraev, Yu.I., Kolesnikova, S.I., Tsvetnitskaya, S.A. (2021) ‘Control of a robot manipulator in conditions of un-certainty’, Tomsk State University J. of Control and Comput. Sci., (57), pp. 4–12 (in Russ.). doi: 10.17223/19988605/57/1.

5. Lebedev, S.K., Kolganov, A.R. (2017) ‘Modification and adjustment of PID controllers for positioning systems of industrial manipulators’, Proc. III All-Russ. Sci. and Pract. Conf Energy and Energy Conservation: Theory and Pract., pp. 1–13 (in Russ.).

6. Ryadchikov, I.V., Gusev, A.A., Sechenev, S.I., Nikulchev, E.V. (2019) ‘A genetic algorithm for searching for parameters of PID regulators of a walking robot stabilization system’, Proc. NNSTU n.a. R.E. Alekseev, (1), pp. 52–60 (in Russ.).

7. Santos, M.C., Molina, L., Carvalho, E.A.N., Freire, E.O., Carvalho, J.G.N., Santos, P.C. (2021) ‘FABRIK-R: An extension developed based on FABRIK for robotics manipulators’, IEEE Access, 9, pp. 53423–53435. doi: 10.1109/ ACCESS.2021.3070693.

8. Kuznetsov, E.A., Ulyanov, S.V. (2022) ‘Developing of intelligent control system for robotic manipulator with several freedom degrees’, System Analysis in Science and Education, (3), pp. 161–179, available at: http://sanse.ru/down-load/477 (accessed March 21, 2024) (in Russ.).

9. Katulin, M.S., Kuznetsov, E.A., Reshetnikov, A.G., Ryabov, A.R., Semashko, S.V., Ulyanov, S.V. (2021) ‘Mecha-nisms of information exchange and knowledge transfer for interaction tasks in the hazard environment of autonomous intellegent robotic systems’, System Analysis in Science and Education, (4), pp 44–62, available at: http://sanse.ru/down-load/450 (accessed March 21, 2024) (in Russ.).

10. Bukhtoyarov, I.V., Koshkina, I.N. (2020) ‘The creation of a PD controller for the quadcopter’, StudNet, (10), available at: https://stud.net.ru/sozdanie-pd-regulyatora-dlya-kvadrokoptera/ (accessed March 21, 2024) (in Russ.).

11. Kravchenko, P.P., Kulikov, L.I., Scherbinin, V.V. (2019) ‘Application of the method of optimized delta-transfor-mations in the control landing problem for an unmanned aerial vehicle’, J. of Comput. and Systems Sci. Int., 58(5), pp. 786–800. doi: 10.1134/S0002338819050093.

12. Sairanov, A.S., Kasatkina, E.V., Nefedov, D.G., Rusyak, I.G. (2019) ‘The application of genetic algorithms for organizational systems management in case of emergency’, Computer Research and Modeling, 11(3), pp. 533–556. doi: 10.20537/2076-7633-2019-11-3-533-556.