Journal influence
Bookmark
Next issue
Mathematical formulation of one-criterion optimization problem of crew actions scheduling on Russian segment of the International space station
The article was published in issue no. № 3, 2013 [ pp. 77-82 ]Abstract:The flight scheduling process is briefly described in the article. It is one of the most important stages of space flight control task solution. Three stages of flight scheduling are given: strategic, tactical and executive. The executive sched-uling is divided into three phases: long-term, short-term anddetailed. The result of each scheduling phase is presented by special plan type: on-orbit operation summary, weekly lookahead plan, short-term plan. The difference of these plan types is in planning interval and data processing depth. The sequence of operator basic actions at placing every next activity into a plan is given. The formal provision of information to create a short-term plan is proposed to take from the following factors: list of planning activities, list of astronauts on the International Space Station (ISS) board, resource data. Themathematical modeling of all required data and restrictions is made. A crew downtime minimization is the selected optimization criterion. Two approaches are used to set up an experiment: the directsearch method and the branch and bound method. An analysis of the algorithms results is made. The conclusions about optimization criterion selection accuracy and ramification rules accord-ing to the branch and bound method are formulated. The future tasks regarding crew activities scheduling process optimiza-tion are defined.
Аннотация:Кратко описан процесс планирования полета, являющийся одним из важнейших этапов решения задачи управления космическим полетом. Приведены три стадии планирования полета: стратегическая, тактическая и исполнитель-ная. В свою очередь, исполнительное планирование делится на долгосрочное, краткосрочное и детальное. Продук-том каждой фазы планирования является определенный типплана: номинальный план полета, общий план сопрово-ждения, детальный план полета. Типы плана отличаются интервалом планирования и глубиной обработки данных. Приводится также последовательность основных действий оператора при включении каждой последующей полет-ной операции в план. Формальное представление информации, на основе которой формируется план полета, предла-гается взять из следующих факторов: списка планируемых полетных операций, состава членов экипажа на борту Международной космической станции, данных о ресурсах.Выполнено математическое представление всех необхо-димых данных и набора ограничений. В качестве оптимизационного критерия выбрана минимизация простоев эки-пажа. Для постановки эксперимента использованы два подхода – метод прямого перебора и метод ветвей и границ. Проведен анализ результатов работы алгоритмов и сформулированы выводы о корректности подборки критерия оптимизации и правил ветвления по методу ветвей и границ. Определены дальнейшие задачи в направлении оптимизации процесса планирования действий экипажа.
| Authors: (nikolai.orlovski@mail.ru) - , Russia, (vsp1999@yandex.ru) - , Russia, Ph.D | |
| Keywords: the branch and bound method, mathematical modeling, optimisation, crew activities, flight operation, planning |
|
| Page views: 12624 |
Print version Full issue in PDF (13.63Mb) Download the cover in PDF (1.39Мб) |
Процесс управления космическим полетом начинается с такого важного этапа, как планирование. Дальнейшие этапы строятся на основе реализации планов и включают осуществление полета, контроль полета, принятие решений по результатам контроля и их выполнение. Планирование космических полетов делится на стратегическое, тактическое и исполнительное. Стратегическое планирование решает задачу определения основных целей полета, проектных параметров бортовых систем, методов управления орбитальным комплексом (ОК) и т.д. На стадии тактического планирования рассчитываются даты стартов транспортных и грузовых кораблей, располагаемые на Международной космической станции (МКС) ресурсы и пределы их расхода, перечень научных экспериментов и др. Исполнительное планирование устанавливает конкретные даты, время, последовательность и методы выполнения полетных операций, приводящих к цели, порядок использования различных средств, входящих в состав системы управления полетом. Длительность периода полета, охваченного тем или иным исполнительным планом, будем называть интервалом планирования. В зависимости от этой величины исполнительное планирование делится на долгосрочное, краткосрочное, детальное. Интервал долгосрочного планирования равен периоду проведения экспедиции, что позволяет определить основные цели для каждой конкретной экспедиции и результаты их выполнения. Продуктом данного вида планирования является номинальный план полета (НПП), представляющий собой список всех основных операций. Так как НПП охватывает значительный интервал полета МКС, степень его точности достаточно низкая. Поэтому вводится краткосрочное планирование, для которого выбран интервал в одну неделю. Результатом является оперативный план полета (ОПП). Он строится в рамках ранее разработанного НПП с учетом реального состояния ОК. ОПП содержит полный перечень операций, подлежащий выполнению на планируемый период времени, с указанием требуемых ресурсов. Для детального планирования величина интервала составляет одни сутки. На этом этапе происходит привязка полетных операций к определенному моменту времени в сутках. Итогом детального планирования является детальный план полета (ДПП) – наиболее подробный руководящий документ. НПП, ОПП и ДПП дополняют друг друга и отличаются глубиной обработки данных и величиной интервала планирования [1]. В процессе разработки планов полета оператор-планировщик решает различного рода задачи, одной из которых является формирование последовательности действий для всех членов экипажа. Оператору для размещения каждой полетной операции требуется выполнить следующие шаги. 1. Выбрать полетную операцию из заявочного списка, поступающего из программы полета, и найти промежуток времени, в рамках которого обеспечиваются допустимые условия ее выполнения. Для этого нужно проанализировать большое количество данных на всем протяжении планируемого интервала, что занимает достаточно много времени и является сложной задачей. 2. Разместить выбранную на предыдущем шаге операцию в подходящем месте и проверить план на отсутствие несовместимостей между работами, а также на соблюдение всех ограничений и правил планирования. Данные основные задачи решаются оператором при планировании действий экипажа Российского сегмента (РС) МКС. Количество полетных операций может составлять несколько сотен единиц, а число космонавтов варьируется от трех до девяти человек. Зачастую встречаются ситуации, когда условия, необходимые для реализации нескольких разнотипных операций, выполняются на одном участке интервала, а доступные ресурсы ОК не обеспечивают возможности их одновременного осуществления. Тогда перед оператором-планировщиком возникает серьезная проблема: какие из конфликтующих операций следует запланировать на данном участке интервала, а какие отложить [2]. Формальное представление информации, на основе которой формируется план полета, может быть выполнено посредством анализа следующих факторов: – список планируемых полетных операций; – состав членов экипажа, находящихся на борту РС МКС, которым предстоит выполнять указанные работы; – данные о затратах всех видов ресурсов, необходимых для реализации каждой заявленной на выполнение полетной операции; – общий объем каждого вида ресурса, имеющегося в наличии на космической станции. Заявленный перечень работ, который необходимо включить в план, может быть представлен в виде множества A={ai},
Матрица D формируется на основе программы полета и описания полетных процедур. Для корректного формирования плана необходима следующая информация: условия проведения каждой полетной операции (поступают из программы полета); совокупность ограничений и правил для проведения полета, которые корректируются на протяжении формирования всех видов планов до момента создания оперативных планов с учетом приобретенного опыта и фактического состояния космического аппарата и наземных комплексов управления (НКУ). Процесс планирования действий экипажа предлагается представить в виде матрицы P={pji},
pnji – время начала выполнения полетной операции; pkji – время окончания выполнения полетной операции. В процессе расчетов также потребуется множество F={fi},
Для облегчения труда оператора задачу оптимизации составления расписания действий экипажа можно решить с применением автоматизации. Для формализации задачи необходимо определить критерий, по которому будет выбираться наилучший вариант плана из некоторого набора, и уточнить ограничения, накладываемые на план [3]. Одним из наиболее важных требований при распределении полетных операций между членами экипажа является максимальная загрузка космонавтов, то есть отсутствие простоев между выполнением запланированных действий. Таким образом, оптимизацию процесса планирования действий экипажа предлагается осуществить через минимизацию простоев экипажа:
где Ij – интервал функционирования космонавта j в минутах (берется из программы полета); В свою очередь, существует набор ограничений и правил планирования, которым должен удовлетворять план. К ним относятся следующие. 1. Суммарное количество каждого ресурса, используемого всеми запланированными полетными операциями, не должно превышать значения, имеющегося на станции:
2. Запланированная полетная операция должна выполняться как минимум одним членом экипажа:
3. Член экипажа должен уметь выполнять назначенную ему работу. В матрице E={eji},
4. Множество O={oi},
Это полетные операции из группы режима труда и отдыха и других групп в зависимости от главной цели плана (стыковка, внекорабельная деятельность, расстыковка):
5. Соответствие общей продолжительности работ в плане, выполняемых космонавтом j, величине интервала функционирования этого космонавта:
6. Отсутствие одновременной реализации нескольких полетных операций одним членом экипажа. Для формирования ограничения следует модифицировать матрицу P в P¢ следующим образом: для каждого ppji=0 значения pnji и pkji приравниваются к ближайшему слева pkji-1, …, n-1, у которого ppji-1, …, n-1=1. Получается, что теперь pn¢ji=pk¢ji¹0, а общая продолжительность работы pk¢ji–pn¢ji=0:
7. Отсутствие одновременного выполнения несовместимых работ в плане:
Необходимо также обеспечить соответствие норм режима труда и отдыха в плане и выполнение всех необходимых условий для проведения каждой включенной в план полетной операции. План, удовлетворяющий всем перечисленным ограничениям, считается допустимым, но в нем не учитывается требование максимально эффективного использования рабочего времени членами экипажа. Для оптимизации процесса планирования исследованы два метода поиска наилучшего плана с использованием предложенного выше критерия: метод прямого перебора и метод ветвей и границ [4]. Прямой перебор использован как точный метод для проверки и подтверждения корректности применения предложенного алгоритма ветвей и границ. Прямой перебор для данной постановки задачи представляет собой рассматриваемую в комбинаторике задачу размещения без повторений. Количество размещений при m=k составляет Метод ветвей и границ позволяет получать оптимальный план за счет отсечения заранее известных, не приводящих к лучшему значению вершин. Блок-схема алгоритма работы метода ветвей и границ, примененного к данной постановке задачи планирования действий экипажа, представлена на рисунке. В указанных алгоритмах приняты следующие ограничения: – суммарное количество каждого ресурса, используемого всеми запланированными полетными операциями, не должно превышать значение, имеющееся на станции; – соответствие общей продолжительности работ в плане, выполняемых каждым космонавтом, величине интервала функционирования этого космонавта. В таблице приведены результаты сравнения времени работы алгоритмов до нахождения оптимального значения при использовании вышеуказанных методов для разного уровня сложности (размерности) задачи. В качестве исходных данных для всех экспериментов использовалась одна и та же детерминированная последовательность полетных операций.
Оба метода дают возможность достигать оптимального качества плана за различное время. Метод ветвей и границ в полной мере удовлетворяет требованию минимизации простоев для всех вариантов тестирования и почти в каждом случае требует на это менее 0,5 сек. Лишь последний тест занял 2,7 сек., что в 451 раз быстрее по сравнению с прямым перебором (1226,31 сек.). Таким образом, на основе полученных данных работы алгоритмов можно сделать вывод о корректности выбора критерия оптимизации, правил и очередности ветвления метода ветвей и границ. В целях дальнейшего повышения качества расписания действий экипажа планируется провести Литература 1. Соловьев В.А., Лысенко Л.Н., Любинский В.Е. Управление космическими полетами. М.: МГТУ им. Н.Э. Баумана, 2009. Ч. I. 476 с. 2. Станиловская В.И. Автоматизация планирования полетов долговременных орбитальных комплексов: дис… канд. технич. наук. Королев, 2008. 198 с. 3. Бахвалов Ю.А. Математическое моделирование: учеб. пособие. Новочеркасск: ЮРГТУ (НПИ), 2010. 142 с. 4. Гончаров Е.Н., Ерзин А.И., Залюбовский В.В. Исследование операций. Примеры и задачи: учеб. пособие. Новосибирск: НГУ, 2005. 78 с. References 1. Solovyov V.A., Lysenko L.N., Lyubinsky V.E., Upravlenie kosmicheskimi polyotami [Spaceflights control], Part 1, Moscow, BMSTU, 2009. 2. Stanilovskaya V.I., Avtomatizatsiya planirovaniya polyotov dolgovremennykh orbitalnykh kompleksov [Flights Scheduling Automation for Long-Term Orbital Complexes], PhD dissertation, Korolyov, 2008. 3. Bakhvalov Yu.A., Matematicheskoe modelirovanie [Mathematical modeling], Novocherkassk, YuRGTU(NPI), 2010. 4. Goncharov E.N., Erzin A.I., Zalyubovsky V.V., Issledovanie operatsy. Primery i zadachi [Operations Research. Examples and exercises], Novosibirsk, NGU, 2005. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Permanent link: http://swsys.ru/index.php?page=article&id=3563&lang=en |
Print version Full issue in PDF (13.63Mb) Download the cover in PDF (1.39Мб) |
| The article was published in issue no. № 3, 2013 [ pp. 77-82 ] |
Perhaps, you might be interested in the following articles of similar topics:
- Математическая постановка многокритериальной задачи оптимизации плана полета
- Метод планирования инновационной деятельности
- Моделирование потока запросов в распределенных вычислительных системах
- Репрезентативность метрик на основе событий процессора Intel Sandy Bridge при анализе времени обработки данных в памяти
- Программный комплекс для расчета процесса нанесения покрытия в псевдоожиженном слое
Back to the list of articles
 , полетных операций, где i – номер полетной операции; m – количество полетных операций. Элемент множества ai содержит длительность полетной операции i. Множество A поступает из программы полета и НПП. Все полетные операции реализуют находящиеся на борту станции участники экспедиции, состоящей из множества B={bj},
, полетных операций, где i – номер полетной операции; m – количество полетных операций. Элемент множества ai содержит длительность полетной операции i. Множество A поступает из программы полета и НПП. Все полетные операции реализуют находящиеся на борту станции участники экспедиции, состоящей из множества B={bj},  , космонавтов (членов экипажа), где j – номер космонавта; n – количество космонавтов. Элемент множества bj содержит идентификатор космонавта j. Множество B поступает из программы полета. На реализацию каждой полетной операции требуется затратить известное количество различных ресурсов. Эти данные хранятся в матрице C={cri},
, космонавтов (членов экипажа), где j – номер космонавта; n – количество космонавтов. Элемент множества bj содержит идентификатор космонавта j. Множество B поступает из программы полета. На реализацию каждой полетной операции требуется затратить известное количество различных ресурсов. Эти данные хранятся в матрице C={cri},  , где r – вид ресурса; R – количество видов ресурса. Элемент матрицы cri – тре- буемое количество ресурса r для выполнения полетной операции i. Матрица C поступает из программы полета. Доступное количество всех видов ресурсов на заданный интервал планирования хранится во множестве Res={resr},
, где r – вид ресурса; R – количество видов ресурса. Элемент матрицы cri – тре- буемое количество ресурса r для выполнения полетной операции i. Матрица C поступает из программы полета. Доступное количество всех видов ресурсов на заданный интервал планирования хранится во множестве Res={resr},  Элемент множества resr отображает оставшийся на борту объем ресурса r. Множество Res поступает из программы полета. Перед началом составления плана полета оператору требуется список полетных операций, не совместимых по времени и/или ресурсам. Такие полетные операции не могут выполняться различными членами экипажа в один и тот же промежуток времени. Их перечень и признак несовместимости хранятся в матрице D={dis},
Элемент множества resr отображает оставшийся на борту объем ресурса r. Множество Res поступает из программы полета. Перед началом составления плана полета оператору требуется список полетных операций, не совместимых по времени и/или ресурсам. Такие полетные операции не могут выполняться различными членами экипажа в один и тот же промежуток времени. Их перечень и признак несовместимости хранятся в матрице D={dis},  , где элемент матрицы
, где элемент матрицы
 , которая задает распределение полетных операций между членами экипажа. Элемент матрицы представляет собой кортеж pji=(ppji, pnji, pkji), где
, которая задает распределение полетных операций между членами экипажа. Элемент матрицы представляет собой кортеж pji=(ppji, pnji, pkji), где

 (1)
(1) – длительность выполнения всех полетных операций космонавтом j.
– длительность выполнения всех полетных операций космонавтом j. (2)
(2) . (3)
. (3) , хранится признак допуска космонавта j к выполнению полетной операции i по результатам тренировок. Элемент матрицы
, хранится признак допуска космонавта j к выполнению полетной операции i по результатам тренировок. Элемент матрицы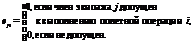

 (4)
(4) (5)
(5) (6)
(6) (7)
(7) вариантов, поэтому уже для m=10 полетных операций в заявочном списке существует более трех миллионов комбинаций.
вариантов, поэтому уже для m=10 полетных операций в заявочном списке существует более трех миллионов комбинаций. исследование возможности и эффективности применения при решении данной задачи методов многокритериальной оптимизации и использование модифицированных генетических алгоритмов.
исследование возможности и эффективности применения при решении данной задачи методов многокритериальной оптимизации и использование модифицированных генетических алгоритмов.