Journal influence
Bookmark
Next issue
Building method of fuzzy semi-markov model of complex system functioning
The article was published in issue no. № 3, 2010Abstract:The article deals with the system functioning analysis on the base of fuzzy semi-Markov models. Different ways of fuzzy introduction are given into semi-Markov models according to the character of using information and solving problems peculiarities of system functioning analysis. A new class of fuzzy semi-Markov models is defined according to the given method of fuzziness introduction into these models. The building method of fuzzy semi-Markov model of system functioning is given.
Аннотация:Анализируется функционирование систем на основе нечетких полумарковских моделей. Рассматриваются различные способы введения нечеткости в полумарковские модели в зависимости от характера используемой информации и особенностей решаемых задач анализа функционирования систем.
| Authors: (byg@yandex.ru) - , Ph.D, Borisov V.V. (BYG@yandex.ru) - Smolensk Branch of the Moscow Power Engineering Institute, Smolensk, Russia, Ph.D, (BYG@yandex.ru) - , Ph.D, Dli M.I. (midli@mail.ru) - (Smolensk Branch of the Moscow Power Engineering Institute, Smolensk, Russia, Ph.D | |
| Keywords: fuzzy representation, fuzzy function, fuzzy conclusion, fuzzy semi-Markov model |
|
| Page views: 17218 |
Print version Full issue in PDF (5.84Mb) Download the cover in PDF (1.43Мб) |
Одним из эффективных инструментов анализа функционирования систем, базирующихся на вероятностном подходе, является использование полумарковских моделей для оценки вероятностей нахождения системы в различных состояниях. Сложность полумарковской модели функционирования системы определяется как множеством учитываемых факторов, так и непростой организацией самой системы (наличием разнородных подсистем, элементов и взаимосвязей между ними). Существенным является также необходимость учета фактора неопределенности анализируемых переменных и случайности событий. Традиционно используемый для учета стохастической неопределенности вероятностный подход в полумарковских моделях не всегда применим из-за недостатка статистической информации о состоянии сложной системы. Кроме того, при традиционном подходе невозможно учесть: · неопределенность переменных, обусловленную экспертным характером значительной части информации или эвристическим описанием процессов; · разнокачественность данных, а также их оценку с помощью различных шкал; · нечеткость выделения и описания переменных или отдельных состояний, а также входных и выходных воздействий. Одним из основных способов решения подобных проблем при анализе функционирования систем является использование нечетких полумарковских моделей [1–3]. Следует отметить определенные ограничения существующих нечетких полумарковских моделей: · не всегда четко обосновано соответствие вложенных цепей полумарковской модели классу цепей Маркова; · имеющиеся модели в общем случае используются только для прогнозирования характеристик пребывания моделируемой системы в заданном состоянии, что затрудняет решение задач управления; · предлагаемые подходы к построению нечетких полумарковских моделей не учитывают наличие избыточности ресурса как необходимое условие функционирования сложной системы. Использование полумарковских моделей для анализа функционирования систем Сложные системы, как правило, характеризуются некоторым уровнем избыточности, позволяющим, с одной стороны, противостоять отказам (или другим повышающим их энтропию явлениям), с другой стороны, накапливать соответствующее этому уровню количество отказов элементов, не приводящее к отказу системы в целом. Для восстановления такой избыточности в системе проводится обслуживание с контролем состояния системы и восстановительными мероприятиями. Формальное описание такого процесса функционирования системы представляется полумарковской моделью (рис. 1).
Учитывая, что Ротк является также и вероятностью перехода из состояния S1 в состояние S2 за один шаг для вложенной марковской цепи, для нее должно выполняться ограничение на отсутствие последействия как основное условие марковости переходов из состояния в состояние. Полумарковский процесс задается с помощью матрицы F(t) условных функций распределения продолжительности пребывания в состояниях, матрицы W переходных вероятностей вложенной марковской цепи и начального состояния процесса, из которого он стартует:
Ненулевые компоненты матрицы F(t) запишутся в следующем виде:
Здесь ТК, ТВ – математические ожидания продолжительностей проведения проверки и восстановления после достоверного обнаружения отказа системы. Безусловные функции распределения Fi(t) определятся в соответствии с выражением Fi(t)= Для рассматриваемого примера получим:
Среднее время пребывания системы в соответствующих состояниях находится следующим образом:
Тогда Финальное распределение вероятностей состояний вложенной марковской цепи определяется в результате решения системы уравнений в матричном виде P=PW, где P – вектор-строка (Р1, Р2, Р3). Эта система уравнений является линейно зависимой, так как для нее выполняется условие нормировки. Таким образом, для рассматриваемого случая получим систему уравнений
Решение этого уравнения имеет следующий вид:
В стационарном режиме распределение вероятностей состояний для полумарковского процесса в целом определяется из выражения
Очевидно, что показателем эффективности системы, функционирование которой описывается с помощью приведенного полумарковского процесса, будет вероятность застать систему в состоянии S1 в произвольный момент. И эта вероятность является функцией периода и продолжительности контроля, то есть ТП и ТК, а также функцией распределения моментов отказа системы Fотк. Выражение этой вероятности имеет вид
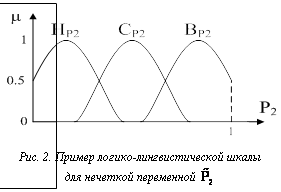
Таким образом, числитель данного выражения соответствует средней продолжительности пребывания системы в исправном состоянии S1, а знаменатель – сумме средних времен пребывания в состоянии исправности, контроля и восстановления. В этой полумарковской модели в отличие от марковской учтены периодичность и продолжительность контроля [4]. Способы введения нечеткости в полумарковские модели Анализ функционирования системы во многом субъективный процесс, в ходе которого требуется учитывать как количественные, так и качественные переменные, плохо поддающиеся формализации. Это затрудняет использование традиционных полумарковских моделей. Кроме того, как отмечалось, сложность использования вероятностного подхода анализа функционирования систем обусловлена уникальностью и сложностью типизации оцениваемых ситуаций и отсутствием достаточных статистических данных. Все это позволяет обосновать целесообразность применения методов теории нечетких множеств и нечетких вычислений при построении и использовании полумарковских моделей. Предлагаются два способа введения нечеткости в полумарковские модели. 1. Дополнение выражения для оценки распределения вероятностей состояний функциями принадлежностей времени пребывания системы в соответствующих состояниях. В этом случае выражение для оценки распределения вероятностей состояний примет следующий вид: 2. Замена вероятностей состояний и времен пребывания системы в соответствующих состояниях на нечеткие числа (нечеткие множества), а обычных операций – на расширенные операции над нечеткими числами; при этом для определения соответствующих нечетких множеств используются нечеткие отображения, реализуемые в соответствии с одним из известных подходов (нечеткие продукции, нечеткие отношения, нечеткие функции). Данный способ введения нечеткости в полумарковскую модель заключается в следующем: · вероятности состояний и времен пребывания системы в соответствующих состояниях заменяются на нечеткие числа (нечеткие множества); · для задания нечетких переменных, характеризующих вероятности состояний и времен пребывания системы в соответствующих состояниях, используются нечеткие отображения, реализуемые в соответствии с одним из подходов (нечеткие продукции, нечеткие отношения, нечеткие функции); · операции суммирования, произведения и деления над вероятностями состояний и времен пребывания системы в соответствующих состояниях заменяются на расширенные (например, по принципу обобщения Л. Заде или на основе интервального метода) операции суммирования, произведения и деления нечетких чисел соответственно. Примечания: 1) использование указанных выше способов введения нечеткости в полумарковские модели зависит от характера используемой информации и особенностей решаемых задач анализа функционирования систем; 2) в предлагаемом методе построения и использования нечеткой полумарковской модели функционирования системы реализован второй способ введения нечеткости в полумарковскую модель. Метод построения нечеткой полумарковской модели функционирования системы Рассмотрим основные этапы предлагаемого метода. Этап 1. Задание нечетких переменных При этом значения вероятностей Pi состояний системы являются базовыми множествами, на ко- торых определены функции принадлежности нечетких множеств, число которых для каждого состояния системы может быть различным. Для наглядности при оценке будем использовать по три нечетких множества (термы {Низкий, Средний, Высокий}) для задания каждой нечеткой переменной Отметим, что, хотя возможно совпадение названий термов для различных нечетких переменных, на самом деле они могут характеризоваться разными параметрами. Для формирования терм-множеств нечетких переменных
где a2, b2 – параметры функции принадлежности колоколообразного типа.
Все значения вероятностей времен mi пребывания системы в соответствующих состояниях являются базовыми множествами, на которых определены функции принадлежности нечетких множеств нечетких переменных Как и для нечетких переменных Этап 3. Задание нечетких отображений для нечетких переменных Исходя из выражений (1) и (2) зададим следующие нечеткие отображения для нечетких переменных Как уже было сказано, нечеткие отображения Рассмотрим пример реализации нечеткого отображения П1: ЕСЛИ П2: ЕСЛИ . . . Пl: ЕСЛИ . . . П9: ЕСЛИ Для нечеткой переменной Этап 4. Задание нечетких отображений для нечетких переменных В соответствии с выражением (3) зададим следующие нечеткие отображения для нечетких переменных Если входную переменную TП представлять как нечеткую переменную Рассмотрим пример реализации нечеткого отображения П1: ЕСЛИ П2: ЕСЛИ П3: ЕСЛИ Далее для нечеткой переменной Если переменная TП является четкой, то для реализации нечеткого отображения Следует отметить, что, поскольку понятия нечеткой функции четкой переменной и нечеткого отношения соответствуют друг другу в математическом смысле, нечеткая функция
Этап 5. Определение значений нечетких переменных, характеризующих распределение вероятностей состояний для нечеткого полумарковского процесса. Для выполнения данного этапа предлагаемого метода введем необходимые понятия, определения и выражения для расчетов. Нечеткое число а) $ xÎR, такое, что б) множества α-уровней нечеткого числа в) $ NÎR, такое, что " xÎR, если |x|≥N, то Операции над нечеткими числами могут выполняться с использованием различных методов. Так, при осуществлении операций над нечеткими числами с использованием интервального арифметического метода интервальные вычисления выполняются над всеми множествами α-уровней этих чисел. Пусть заданы два нечетких числа Интервальные операции над множествами α-уровней нечетких чисел Сложение:
Умножение:
Деление:
где Примечание: чтобы отличить арифметические операции над нечеткими числами от обычных арифметических операций, обозначим символами По другому методу выполнения вычислений, основанному на принципе расширения Л. Заде, произвольная расширенная бинарная арифметическая операция
где Тогда, например, расширенная операция произведения
Примечание: в дальнейшем при осуществлении операций над нечеткими числами будем использовать интервальный арифметический метод над множествами α-уровней этих чисел. Для задания правил вывода на основе нечеткой байесовой сети рассмотрим понятия нечеткой вероятностной меры и нечеткого вероятностного пространства. Функция а) 0x б) в) если A и B являются несовместными значениями из e (то есть AÇB=Æ), то г) если A и B являются событиями из e, то
Здесь W=Rm – некоторое универсальное множество, на котором задана переменная A; e – множество несовместных значений переменной A; F(R) – множество всех нечетких чисел, определенных на множестве действительных чисел R; 0x и 1x – нечеткие числа 0 и 1. Нечетким вероятностным пространством называется тройка Таким образом, в основе предлагаемого метода построения и использования нечеткой полумарковской модели лежит следующее выражение:
где В заключение отметим, что в данной работе делается анализ функционирования систем на основе нечетких полумарковских моделей. Предложены различные способы введения нечеткости в полумарковские модели в зависимости от характера используемой информации и особенностей решаемых задач анализа функционирования систем. Разработан новый класс нечетких полумарковских моделей с учетом предложенного способа введения нечеткости в эти модели. Предложен метод построения и использования нечеткой полумарковской модели функционирования системы. Литература 1. Bhattacharyya M. Fuzzy Markovian decision process // Fuzzy Sets and Systems. Vol. 99, 1998, pp. 273–282. 2. Praba B., Sujatha R., Srikrishna S. Fuzzy reliability measures of fuzzy probabilistic semi-Markov model // Int. Journal of Recent Trend in Engineering. Vol. 2, No. 2, 2009, pp. 25–29. 3. Praba B., Sujatha R., Srikrishna S. A study on homogeneous fuzzy semi-Markov model // Applied Mathematical Sciences. Vol. 3, No 50, 2009, pp. 2453–2467. 4. Бояринов Ю.Г., Дли М.И., Круглов В.В. Оценка диапазона возможных значений вероятности пребывания в заданном состоянии марковской модели производственно-экономической системы // Программные продукты и системы. 2009. № 4. С. 88–91. 5. Круглов В.В., Борисов В.В. Искусственные нейронные сети. Теория и практика. М.: Горячая линия – ТЕЛЕКОМ, 2002. 6. Moore R. E. Interval analysis. New Jersey: Prentice Hall, 1966. 7. Kwakernaak H. Fuzzy random variables: definitions and theorems // Information Sciences. № 15(1), 1978, pp. 1–29. |
| Permanent link: http://swsys.ru/index.php?id=2552&lang=en&page=article |
Print version Full issue in PDF (5.84Mb) Download the cover in PDF (1.43Мб) |
| The article was published in issue no. № 3, 2010 |
Perhaps, you might be interested in the following articles of similar topics:
- Полумарковские модели систем с нечеткими параметрами
- Косвенный метод нечеткого вывода для продукционных систем со многими входами
- Архитектура подсистемы нечеткого вывода для оптимизатора баз знаний
- Модель принятия решений целеустремленного поведения агента в слабоструктурированных средах
- Механизмы управления эволюцией организационно-технологической системы
Back to the list of articles
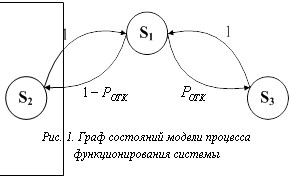 На рисунке S1 – состояние применения системы по назначению (желаемое состояние); S2 – состояние проверки работоспособности системы (пригодности к использованию по назначению); S3 – состояние проверки непригодности (отказа) к использованию по назначению, а также восстановление до состояния пригодности (готовности) к использованию по назначению после обнаружения дефекта (отказа); Ротк – вероятность возникновения отказа системы, Ротк=Fотк(ТП); Fотк(ТП)= =Вер(tотк<ТП) – функция распределения случайной величины tотк момента отказа, соответствующая значению tотк<ТП, то есть вероятности отказа в течение периода проверки системы TП.
На рисунке S1 – состояние применения системы по назначению (желаемое состояние); S2 – состояние проверки работоспособности системы (пригодности к использованию по назначению); S3 – состояние проверки непригодности (отказа) к использованию по назначению, а также восстановление до состояния пригодности (готовности) к использованию по назначению после обнаружения дефекта (отказа); Ротк – вероятность возникновения отказа системы, Ротк=Fотк(ТП); Fотк(ТП)= =Вер(tотк<ТП) – функция распределения случайной величины tотк момента отказа, соответствующая значению tотк<ТП, то есть вероятности отказа в течение периода проверки системы TП. ;
; .
.



 , где ωij – вероятность перехода вложенной марковской цепи за один шаг.
, где ωij – вероятность перехода вложенной марковской цепи за один шаг.
 (1)
(1)
 (2)
(2) m2=TK; m3=TK+TB.
m2=TK; m3=TK+TB.
 (3)
(3)


 на базовых множествах значений вероятностей Pi состояний системы.
на базовых множествах значений вероятностей Pi состояний системы. – НP1, СP1, ВP1; для
– НP1, СP1, ВP1; для  – НP2, СP2, ВP2; для
– НP2, СP2, ВP2; для  – НP3, СP3, ВP3. С одной стороны, это не нарушает общности при рассмотрении предлагаемой нечеткой полумарковской модели (то есть при необходимости перечень термов для каждой нечеткой переменной
– НP3, СP3, ВP3. С одной стороны, это не нарушает общности при рассмотрении предлагаемой нечеткой полумарковской модели (то есть при необходимости перечень термов для каждой нечеткой переменной 
 Этап 2. Задание нечетких переменных
Этап 2. Задание нечетких переменных  на базовых множествах значений вероятностей mi времен пребывания системы в соответствующих состояниях.
на базовых множествах значений вероятностей mi времен пребывания системы в соответствующих состояниях. – Нm1, Сm1, Вm1; для
– Нm1, Сm1, Вm1; для  – Нm2, Сm2, Вm2; для
– Нm2, Сm2, Вm2; для  – Нm3, Сm3, Вm3 (аналогично этапу 1).
– Нm3, Сm3, Вm3 (аналогично этапу 1).
 где
где  – нечеткое отображение.
– нечеткое отображение. для нечеткой переменной
для нечеткой переменной  – НК, СК, ВК; для
– НК, СК, ВК; для  – НВ, СВ, ВВ:
– НВ, СВ, ВВ:
 где
где  – нечеткое отображение.
– нечеткое отображение. , то нечеткое отображение
, то нечеткое отображение  можно реализовать на основе нечеткой продукционной модели SISO-типа (Single Inputs, Single Outputs).
можно реализовать на основе нечеткой продукционной модели SISO-типа (Single Inputs, Single Outputs). для нечеткой переменной
для нечеткой переменной  .
. и определена следующим образом:
и определена следующим образом:
 определяется как нечеткое множество, заданное на множестве действительных чисел R с функцией принадлежности
определяется как нечеткое множество, заданное на множестве действительных чисел R с функцией принадлежности  , где xÎR, и для которого выполняются следующие условия:
, где xÎR, и для которого выполняются следующие условия: ;
; =[a, b]={x/
=[a, b]={x/ ≥α};
≥α}; , а также множества их α-уровней
, а также множества их α-уровней  =[c, d]={x/
=[c, d]={x/ .
.

 .
. ,
,  ,
,  операции нечеткого сложения, умножения и деления соответственно.
операции нечеткого сложения, умножения и деления соответственно. над нечеткими числами может быть задана следующим образом:
над нечеткими числами может быть задана следующим образом:
 – нечеткие числа,
– нечеткие числа,  и
и  имеет следующий вид:
имеет следующий вид:
 : e®F(R) называется нечеткой вероятностной мерой [7] на (W, e) в том и только в том случае, если:
: e®F(R) называется нечеткой вероятностной мерой [7] на (W, e) в том и только в том случае, если:

 =1x и
=1x и  =0x;
=0x; Ê Ê
Ê Ê ;
;
 .
. (4)
(4) – нечеткая переменная, характеризующая распределение вероятностей состояний для нечеткого полумарковского процесса.
– нечеткая переменная, характеризующая распределение вероятностей состояний для нечеткого полумарковского процесса.