Software & Systems

В работе рассматривается многослойный персептрон, структуру которого образуют множество сенсорных элементов (входных узлов или узлов источника), составляющих входной слой, один или несколько скрытых слоев вычислительных нейронов (ассоциативные элементы) и один выходной слой нейронов (реагирующие элементы). Входной сигнал распространяется по сети прямо, от слоя к слою (рис. 1). Таким образом, персептроны позволяют построить отображение между входными сигналами и необходимой реакцией на выходе.

Многослойные персептроны успешно применяются для решения разнообразных сложных задач, таких как прогнозирование, классификация, сжатие информации, ассоциативная память и т.д. Особенно много прикладных задач решается с помощью многослойных персептронов в области финансовых рынков: классификация и анализ временных рядов; прогнозирование, оптимизация товарных и денежных потоков; прогнозирование налоговых поступлений; расчет цен опционов; оценка индексов курсов акций и др.

Рассмотрим разработку ПО, в основу которого положена математическая модель полносвязного многослойного персептрона, предназначенного для автоматизации проектирования искусственной нейронной сети при решении прикладных задач, причем основными входными данными являются элементы обучающей выборки.

Сначала проанализируем этапы проектирования искусственной нейронной сети, выявим их особенности, чтобы определить возможности автоматизации [1].

Предварительная обработка данных. Реальные данные могут содержать шумы и часто неравномерно распределены в пространстве признаков. Для успешного решения проблемы необходимо провести предварительную обработку данных, включающую сбор данных, их анализ и очистку, преобразование данных с целью сделать входную информацию более содержательной и удобной для сети.

Сбор данных. Главное на этом этапе – выбор признаков для описания моделируемого про­цесса. Аналитик должен представлять возможные связи между признаками и ясно понимать суть задачи. После того как признаки выбраны, нужно установить, значимы они или отражают другие существенные признаки. Однако следует понимать, что время обучения многослойного персептрона быстро возрастает с увеличением числа входов, при этом существенно уменьшается экстраполяционная способность сети.

Среди методов, позволяющих осуществить хороший отбор признаков, можно выделить кросс-корреляционный и факторный анализы, понижение размерности с использованием самой сети, генетические и box-counting-алгоритмы, вейвлет-разложение.

Заметим, что сокращение числа признаков позволяет справиться с еще одной проблемой – дефицит примеров для обучения. Если их недостаточно, можно воспользоваться методом искусственных примеров.

Очистка и преобразование данных. Основная цель преобразования данных в том, чтобы они измерялись в одних единицах и варьировались в разумных пределах, например, в интервале [0, 1] (или [-1, 1]). При отсутствии этих свойств лучше использовать безразмерные данные, выполнив определенные преобразования, например линейные, с помощью статистических характеристик, ло- гистической функции или функции активации нейронов и т.д. Также полезными будут определенные комбинации признаков, такие как произведения, частные и др. Часто с их помощью можно получить более простую модель.

Построение модели. На данном этапе решаются следующие задачи:

–    выбор топологии сети (число нейронов, число скрытых слоев, структура связей);

–    выбор функции активации нейронов;

–    определение весов нейронов.

Главной проблемой в решении задач с помощью искусственной нейронной сети остается определение ее топологии или аналитиком в ручном режиме, или автоматически на основе имеющихся данных с применением конструктивного либо деструктивного подхода [1, 2].

Немаловажную роль в успешном обучении сети играет активационная функция нейронов. Анализ литературы [2, 3] позволяет определить наиболее часто используемые функции активации: сигмовидная с выходными значениями в промежутках [0, 1] и [-1, 1], рациональная сигмовидная, гиперболический тангенс, логарифмическая, гауссовская, радиально-симметричная, пороговая, многопороговая, тождественная (линейная), линейная с насыщением, биполярная.

Выделим среди перечисленных функций сигмовидную, которая      часто применяется благодаря ее преимуществам – способности эффективно вычислять производную и ограничивать выходное значение. Использование нечетких функций увеличивает скорость сходимости. Примером может служить гиперболический тангенс, а добавление к нему небольшого линейного слагаемого  позволяет предотвратить эффект паралича сети. Применяются и другие медленно растущие функции, например . 

Следующая задача – определение веса нейронов – решается с помощью алгоритма обучения, который представляет собой итерационный процесс коррекции синаптических весов: wk+1=wk+ +hkpk, где вектор pk задает направление движения, hk – размер шага, k – номер итерации.

В основе практически всех алгоритмов обучения лежит оптимизационная задача, а алгоритм обучения является алгоритмом ее решения. В связи с этим необходимо выбрать направление движения и шаг. Обычно для выбора используются градиентные методы и методы случайного поиска. Для декомпозиции сложной задачи обучения применяется хорошо известный алгоритм обратного распространения ошибки.

В целом методы обучения можно классифицировать следующим образом [2]:

·     методы нулевого порядка (алгоритм случайного поиска, метод покоординатного спуска, метод многогранника и т.д.);

·     методы первого порядка (простой градиентный спуск, методы сопряженных градиентов, метод ПАРТАН, BFGS с конечной памятью, комбинированный алгоритм случайного поиска и статистического градиента, RProp, QuiqProp, Delta-delta, Delta-bar-delta и т.д.);

·     методы второго порядка (методы Ньютона, Ньютона–Гаусса, Левенберга–Марквардта, а также алгоритмы квазиньютоновского типа, Relax, Relch);

·     нелокальные модификации одноточечных методов (имитация отжига, метод прыгучего шарика, метод СПП, то есть спуск–подъем–перевал, туннельный алгоритм).

Поскольку целевая функция в задачах обучения многоэкстремальная, для нахождения глобального экстремума используются методы ре- стартов, облака, поколений, модифицированный метод многогранника и генетические алгоритмы.

Выбор величины шага имеет ключевое значение для успешной работы обучающего алгоритма. При слишком маленьком шаге обучение будет медленным, а вероятность попадания в локальный минимум большой. Наоборот, при слишком большом шаге можно проскочить мимо глобального минимума. То, какой шаг следует считать малым, а какой большим, в значительной степени зависит от топологии сети и обучающих данных. Самый простой способ выбрать шаг – задать его постоянным. Однако этот метод плохо учитывает особенности минимизируемой функции и многие алгоритмы обучения требуют более точного выбора шага. Наиболее удачными алгоритмами выбора шага считаются методы плавающего шага, параболы и глобальной одномерной оптимизации.

Перед тем как приступить к обучению искусственной нейронной сети, необходимо задать ее начальное состояние. От того, насколько удачно будут выбраны начальные значения весовых коэффициентов, зависит время обучения. Как правило, всем весам на этом этапе присваиваются случайные величины, равномерно распределенные в диапазоне [-A, A]. Однако, как показали эксперименты, данное решение не является наилучшим. В качестве альтернативы предлагается использовать другие виды начальной инициализации – нормальное распределение и методики Nguyen и Widrow [3]. Предложенные методики позволят на практике добиться лучших результатов в сравнении с равномерной инициализацией весов.

Следующим этапом является проверка модели на адекватность реальным данным, то есть необходимо оценить, как искусственная нейронная сеть будет обрабатывать примеры, которые не входили в обучающую выборку. Проверка работоспособности модели на контрольных примерах осуществляется за счет использования разнообразных статистических критериев согласия. Если результаты не удовлетворяют критериям согласия, следует включить тестовые примеры в обучающую выборку и повторить обучение искусственной нейронной сети на расширенной выборке.

В связи с этим желательно получить несме­щенную оценку способности к обобщению. Это можно сделать с помощью процедуры последовательного спуска (с подтверждающим множеством), N-кратного перекрестного подтверждения или обобщенного перекрестного подтверждения (GCV). Можно использовать и более мощные информационные критерии (IС), включающие в себя компоненту, соответствующую критерию согласия, и компоненту штрафа, учитывающую объем обучающего множества и число свободных параметров. В связи с этим Барроном были пред­ложены следующие информационные критерии: нормализованный IС Акаике (NAIC), нормализованный байесовский IС (NBIC) и итоговая ошибка прогноза (FPE).

Для получения более точных результатов работы нейросети можно сформировать ассамблею нейроэкспертов (нейросетей), в которой используется интегральная оценка.

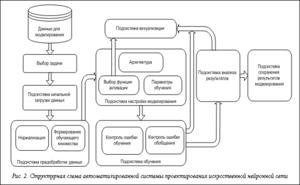
Автоматизированная система проектирования искусственной  нейронной сети. В результате проведенного обзора и анализа факторов, снижающих качество работоспособности искусственной нейронной сети, связанных как с этапом предварительного анализа и подготовки входного вектора данных, так и непосредственно с этапом нейросетевого моделирования, разработана концептуальная схема автоматизированной системы проектирования искусственной нейронной сети (рис. 2) [4]. Работа с автоматизированной системой проектирования должна ограничиваться выбором типа задачи (прогнозирование или классификация), вводом исходных данных, анализом полученных результатов.

Предложенная схема реализована на языке высокого уровня C# с применением объектно-ори­ентированного подхода в среде разработки Microsoft Visual Studio 2008 Express Edition.

В силу сложности автоматизированной системы проектирования искусственной нейронной сети приведем лишь основные классы объектной модели.

1.   Классы, отвечающие за загрузку данных (abstract DataLoader, DataTxtLoader, DataExcel­Loader): реализуют процесс формирования исходных данных для искусственной нейронной сети, преобразовывая данные из файла форматов txt и xls с исходной информацией в вид, приемлемый для подачи на вход сети. В итоге после преобразования все данные для обучения содержатся в объектах типа DataTable (InputData, TargetData), которые в дальнейшем служат для формирования обучаемого, тестового и контрольных множеств (TrainData, TestData, ControlData).

2.   Классы, отвечающие за пред- и постобработку данных (abstract Normalization, Normaliza­tionLogistic, NormalizationLinear, NormalizationDis­persion, NormalizationNone): реализуют способы нормализации – линейный, с помощью статистического преобразования, с помощью логистической функции. Нормализация и денормализация осуществляются методами Normalaze(double x) и DeNormalaze(double y).

3.   Классы, отвечающие за архитектуру сети (Net, Layer, Neuron). После создания объекта класса Net формируются списки слоев List layers и нейронов List neurons, а также вызывается конструктор, который строит архитектуру сети по умолчанию. Список слоев находится на уровне класса Net, а список нейронов на уровне класса Layer. В результате можно увеличивать или уменьшать количество слоев и нейронов благодаря реализованной функции Init(), обращаясь к объекту класса Net. Автоматический подбор количества нейронов скрытого слоя происходит на основании теоремы Хехт–Нильсена, которая переносит результаты теоремы Колмогорова–Арноль­да на искусственные нейронные сети.

4.   Классы, отвечающие за активационные функции (abstract Activation, ActivationImaginary, ActivationZeroWeight, ActivationSigmoid, Activation­Gauss, ActivationHyperbolicTangent): содержат параметры и методы расчета  значений этих функций. Классы ActivationImaginary, ActivationZero­Weight являются служебными и необходимы для работы с входным слоем и нейронами смещения.

5.   Классы, отвечающие за первичную инициализацию весов (abstract InitWeights, InitWeights­Uniform, InitWeightsNormal, InitWeightsWidrow, InitWeightsSegment).

6.   Классы, отвечающие за критерии согласия и информационные критерии. Первая группа классов, наследованных от абстрактного класса PerformanceMesure, реализует критерии согласия. Вторая группа классов, наследованных от абстрактного класса ComplexityPenalty, реализует штрафные слагаемые, используемые при регуля­ризации сложности [3] и в расчете информацион­ных критериев.

7.   Классы, отвечающие за учителей искусственной нейронной сети, в зависимости от типа задачи: классификации или прогнозирования (abstract Trainer, TrainerClassification, TrainerPre­dication). С помощью метода Training () организуется вся логика обучения. Для этого используются два метода класса Net – GoForward(DataVector input) и GoBack(DataVector target), реализующие прямой и обратный проходы алгоритма обратного распространения ошибки.

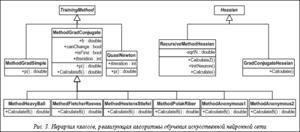
8.   Классы, отвечающие за алгоритмы обучения искусственной нейронной сети (методы оптимизации функции ошибки). Реализованы следующие методы: простой градиентный спуск, методы сопряженных градиентов и квазиньютоновские. Классы, наследуемые от абстрактного класса Hessian, реализуют расчет матрицы Гессе, используемой в квазиньютоновских методах и при реализации прореживания синаптических весов искусственной нейронной сети.

На рисунке 3 приведена иерархия классов, относящихся к алгоритмам обучения искусственной нейронной сети как к наиболее сложным элементам математического обеспечения.

В целом объектная модель системы состоит из 94 классов. Расширяемость созданной объектной модели позволяет добавлять новые функциональные возможности, такие как алгоритмы обучения, функции активации и др. Данный набор классов является основной программной структурой системы, на базе которой строится пользовательский интерфейс.

В результате разработки системы реализованы: ввод данных; автоматический подбор размера окна для задачи прогнозирования; создание многослойной архитектуры сети; автоматический подбор количества нейронов скрытого слоя; нормализация входов и выходов сети; выделение обучаемого, тестируемого и контрольных множеств; выбор функции активации нейрона, алгоритма обучения, а также метода расчета шага; задание параметров обучения; прореживание связей сети; проверка адекватности сети; описание конфигурации системы; формирование ассамблеи сетей; сохранение конфигурации системы и использование ее в дальнейшем; выгрузка результатов решения задачи.

Искусственная нейронная сеть представляет собой хорошо распараллеливающуюся структуру. Это дает возможность решать поставленные задачи намного быстрее, чем при использовании последовательного подхода. Распределенные вычисления могут производиться двумя способами: одна и та же сеть обучается на многих компьютерах сразу; отдельные части сети и (или) источники и потребители данных находятся далеко друг от друга, образуя распределенную систему.

Приведем пример решения задачи прогнозирования выручки от продажи продукции предприятия.

Финансовое прогнозирование является одной из основных задач, решаемых с помощью искусственных нейронных сетей, поэтому для тестирования разработанной системы сделан прогноз выручки одного из крупных предприятий юга России. Подобный анализ необходим в ходе мониторинга банками кредитного риска заемщиков. В качестве данных выбран временной ряд, содержащий значения выручки предприятия с 01.04.2006 по 01.01.2009 с интервалом 1 квартал (итого 12 наблюдений). Выполнен прогноз на 01.04.2009 и 01.07.2009 и сопоставлен с уже имеющимися данными (см. табл.).

Отметим, что прогноз был достаточно точным при таком небольшом объеме исходных данных. Прогноз на 01.04.2009 оказался точнее, чем на 01.07.2009. Это связано с тем, что при проведении многошагового прогнозирования в качестве исходных данных берутся спрогнозированные значения, вследствие чего накапливается ошибка. Ошибка на обучающем множестве составила 1,4 %. Следует отметить, что в ходе экспериментов с разработанной системой NeuroNADS [5] была получена ассамблея сетей, на основании которых и определялись окончательные результаты.

Результаты прогнозирования

Таким образом, в работе предложена система автоматизированного проектирования искусственной нейронной сети для решения прикладных задач, на основе которой разработано ПО NeuroNADS. С его помощью решена задача прогнозирования. Полученные результаты демонстрируют адекватность применения ассамблеи искусственных нейронных сетей в качестве математических моделей исследования в банковском секторе. Применение указанной методики и ПО позволит повысить эффективность прогнозирования финансово-экономических показателей деятельности заемщиков банка и принятия на основе указанных прогнозов решений по минимизации факторов риска заемщиков.

Литература

1.   Бэстен Д.-Э. [и др.]. Нейронные сети и финансовые рынки. М.: ТВП, 1997. 236 с.

2.   Тархов Д.А. Нейронные сети. Модели и алгоритмы. М.: Радиотехника, 2005. 256 с.

3.   Хайкин С. Нейронные сети: полный курс; 2-е изд. М.: Издат. дом «Вильямс», 2006. 1104 с.

4.   Пучков Е.В. Разработка среды моделирования искусственных нейронных сетей. Решение задачи прогнозирования  временного ряда // Вестн. РГУПС. 2009. № 2. С. 44–50.

5.   URL: http://www.i-intellect.ru (дата обращения: 30.05.2010).