Software & Systems

В данной работе рассматривается способ повышения надежности и адаптивности систем автоматического управления (САУ) с помощью специального программного инструментария – оптимизатора баз знаний (ОБЗ) на мягких вычислениях [1]. Использование ОБЗ позволяет уменьшить время проектирования интеллектуальной системы управления (ИСУ), повысить робастность и устранить субъективизм при формировании БЗ нечеткого регулятора (НР). Управление неустойчивым динамическим объектом типа «каретка – перевернутый маятник» является одной из типовых задач в теории управления, так как ее решение наглядно демонстрирует качество САУ. Задача управления состоит в том, чтобы, воздействуя с помощью силы управления на тележку, удерживать маятник в вертикальном положении (угол отклонения оси маятника от вертикали близок к 0) в условиях изменения условий среды функционирования.

Такая задача часто решается с использованием традиционной САУ на основе пропорционально-интегрально-дифференциального регулятора (ПИД-регулятора) в контуре управления [2, 3]. Если коэффициенты усиления регулятора являются постоянными величинами, то система управления не обеспечивает достаточной робастности. В этом случае система неспособна функционировать в нештатных и непредвиденных ситуациях и демонстрирует недостаточную эффективность управления [1].

Обычно настройка регуляторов сопровождается большим количеством экспериментов и множеством осложнений, связанных с неопределенностью некоторых параметров системы, наличием помех в каналах измерения и системе управления. Во многих работах отражена возможность использования различных интеллектуальных методов – нейронных сетей [4] и генетических алгоритмов [5, 6]. В данной работе отражены особенности применения нечетких регуляторов в контуре управления в реальном времени.

Оптимизатор БЗ

Применительно к проектированию ИСУ мягкие вычисления представляют собой комбинацию из следующих подходов: теория нечетких систем, генетические алгоритмы (ГА) и нечеткие нейронные сети (ННС).

НР является центральным элементом ИСУ и вырабатывает управляющие сигналы изменения во времени (законы управления) коэффициентами усиления kp, kd, ki ПИД-регулятора. Ядро НР основано на процессе проектирования БЗ, интегрированной в интеллектуальный контроллер. Структурно БЗ состоит из продукционных логических правил, которые включают нечеткие входные и выходные значения функции принадлежности лингвистических переменных. Функциональная структура ИСУ с блоками НР и ОБЗ на мягких вычислениях представлена на рисунке 1.

Такая структура обладает следующими качествами управления: управляемость, точность и устойчивость (нижний уровень управления – САУ); обучение и адаптация (верхний интеллектуальный уровень управления – НР с БЗ).

Наиболее актуальной проблемой при создании ИСУ является получение оптимальной робастной БЗ, которая гарантирует достижение требуемого уровня качества управления. При проектировании БЗ возникают трудности, связанные со сложностью динамической системы и наличием шумов в системе измерения и управления.

В данной работе рассматривается возможность подключения физического удаленного ОУ для настройки БЗ в НР в режиме реального времени на основе ОБЗ.

Входом ОБЗ является обучающий сигнал, который может быть получен либо на этапе стохастического моделирования поведения ОУ (с использованием его математической модели), либо экспериментально, то есть непосредственно из результатов измерений динамических параметров физической модели ОУ.

Обучающий сигнал является источником знаний и представляет собой массив данных, разделенный на входные и выходные составляющие, каждая из которых, в свою очередь, состоит из одного и более сигналов. В общем виде каждый из составляющих сигналов является выборочной (репрезентативной) траекторией некоторого случайного процесса. При этом подразумевается, что в каждый момент времени существует некоторая корреляция между входными и выходными сигналами. Например, в случае аппроксимации некоторого управляющего сигнала входными компонентами могут являться ошибка управления, интеграл ошибки и ее производная, а выходным компонентом – требуемое значение управляющего воздействия либо некоторые настраиваемые параметры системы управления, например коэффициенты усиления ПИД.

В таком случае входными данными для НР является вектор ошибки, который состоит из ошибки управления e(t), интеграла ошибки управления  и скорости изменения ошибки управления  Выходными данными НР является вектор, состоящий из значений коэффициентов усиления kp, kd, ki ПИД-регулятора, формирующих управляющее воздействие в виде

.      (1)

Структурно ОБЗ состоит из взаимосвязанных генетических алгоритмов (ГА1, ГА2, ГА3), оптимизирующих отдельные компоненты БЗ. Базовые шаги оптимизации и структура ОБЗ подробно описаны в [1].

Результатом аппроксимации обучающего сигнала является построенная БЗ для НР, включающая оптимальное конечное множество правил и оптимально сформированные параметры функции принадлежности входных и выходных переменных НР.

Таким образом, результатом проектирования является требуемый тип универсального аппроксиматора в виде НР с оптимальной структурой БЗ.

Объект управления

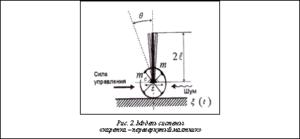
Управление объектом типа «каретка – перевернутый маятник» является одной из типовых задач в теории управления, решение которой наглядно демонстрирует качество САУ. Рассмотрим динамику модели в виде одноосевой каретки (рис. 2) с перевернутым маятником, закрепленным на оси.

Динамика этого ОУ описывается системой дифференциальных уравнений второго порядка, выводимых с учетом сил трения и упругости каретки из баланса моментов и проекций сил на горизонтальную ось Z:

.(2)

Уравнения для скорости производства энтропии следующие:

                                (3)

В уравнениях (2) и (3) z и q – обобщенные координаты; g – ускорение свободного падения (9,8 м/с2); mc – масса тележки; m – масса перевернутого маятника (называемого «шест»); l – половина длины маятника; k и a1 – коэффициенты трения в z и q соответственно; a2 – сила упругости тележки; x(t) – внешний стохастический шум; u – сила управления.

Динамическая система обладает глобальной динамической неустойчивостью, при отсутствии управляющей силы происходит неограниченный рост угла отклонения, то есть маятник падает. Задача управления системой состоит в том, чтобы, воздействуя с помощью силы управления на тележку, удерживать (стабилизировать) маятник в вертикальном положении (угол отклонения оси маятника от вертикали к 0) в условиях изменения среды функционирования.

На рисунке 3 представлены макет, используемый для тестирования технологий проектирования ИСАУ с использованием ОБЗ (а), и стенд для проведения экспериментов (б). Отметим, что данный тип робота является типовым Benchmark для тестирования программного инструментария робастного интеллектуального управления, примеры аналогов которого приведены в [7–10].

Стенд оборудован различными покрытиями для проведения экспериментов с макетом, в том числе в непредвиденных ситуациях управления. На стенде также имеется возможность устанавливать определенный начальный угол для запуска макета.

Интерфейсы ОБЗ

Взаимодействие ОБЗ с ОУ реализуется через модули Matlab/Simulink для математических моделей и СОМ-интерфейс для реальных объектов управления.

Возможность дистанционного проектирования робастных ИСУ (на основе удаленного соединения с ОУ) для настройки БЗ НР на основе ОБЗ с применением технологии мягких вычислений подробно рассмотрена в [11]. Это позволяет проектировать ИСУ без использования системы стохастического моделирования, что дает преимущество при проектировании нечетких систем управления для сложных и слабо формализованных ОУ в непредвиденных ситуациях управления. Реализация физической среды соединения предполагает использование дополнительного оборудования для приема-передачи данных, например, радиоканала Bluetooth, Wi-Fi, или подключение по кабелю, к примеру USB. Профиль соединения использует последовательный порт. Скорость передачи в нашем случае составляет 115 200 бит/сек. В процессе функционирования по COM-порту передаются числа с плавающей точкой в символьном виде. Предполагается обмен информацией между системой управления и ОБЗ для формирования БЗ (рис. 4).

Рассмотрим подробнее процесс настройки функционирования подобной системы (рис. 5). Система управления считывает показания датчиков и отправляет их на компьютер для последующей обработки. Приняв входные значения, ОБЗ оценивает предыдущее решение (БЗ НР) и осуществляет нечеткий вывод для проверки следующего решения (БЗ НР). Результат нечеткого вывода отправляется на удаленное устройство. После этого система управления, обработав входные значения, вырабатывает управляющее воздействие.

Прежде чем приступить к установке соединения между оптимизатором и системой управления, необходимо установить физические ограничения взаимодействующих устройств, то есть определить максимальные и минимальные временные границы одного такта системы управления с учетом приема, передачи и обработки сообщений.

Моделирование и эксперимент

Исследование качества управления ПИД-регу­лятора и нечетких регуляторов на основе программного инструментария ОБЗ проводилось с использованием математической модели и/или реального ОУ. Регуляторы разрабатывались для функционирования в типовой ситуации управления. В таблице 1 приведено сравнение БЗ по количеству правил, количеству функций принадлежности лингвистической переменной и способу оптимизации в программном инструментарии ОБЗ.

Таблица 1

Сравнение БЗ

Параметры математической модели, используемой для моделирования, представлены в таблице 2.

Для сравнения робастности разработанных систем управления используем непредвиденную ситуацию управления. Ситуация моделируется наличием шума в коэффициентах трения, в управляющем воздействии, в системе измерения. В качестве такого шума в эксперименте используется специальное покрытие, а для моделей были установлены соответствующие значения параметров.

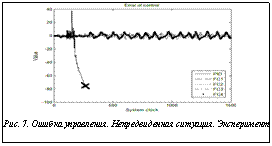
Рассмотрим поведение ПИД-регуляторов и нечетких регуляторов в типичной и непредвиденной ситуациях управления (рис. 6, 7).

Разработанный с использованием математической модели для типовой ситуации управления НР2 (FC2) справился с задачей управления лучше всех, что подтверждено результатами моделирования и эксперимента.

Таблица 2

Ситуации управления, параметры математических моделей

Таким образом, результаты эксперимента показывают, что нечеткие регуляторы, БЗ которых спроектированы по разработанной методологии, обладают повышенной робастностью и способны справляться с задачей управления в широком классе непредвиденных ситуаций [11, 12].

В заключение отметим, что классические системы управления не всегда успешно справляются с задачей управления в случае, если ОУ является глобально неустойчивым или существенно нелинейным, при наличии шумов или времени задержки в каналах измерения, а также при наличии стохастических шумов, особенно типа рэлеевских (с несимметричной функцией плотности распределения вероятностей).

Нечеткие контроллеры, основанные на традиционных инструментариях мягких вычислений, в которых структура ННС строится вручную экспертом или ННС типа ANFIS, уступают по качеству управления и робастности нечетким контроллерам, построенным на основе ОБЗ.

Результаты моделирования широкого класса объектов управления показали, что разработанная технология проектирования ИСУ на основе инструментария ОБЗ демонстрирует хорошие качества управления и робастность, несмотря на изменения (непредсказуемость) широкого класса факторов, таких как изменение внешних шумов, изменение параметров модели ОУ, изменение времени задержки в каналах измерения или изменение цели управления.

Литература

1.     Ульянов С.В., Литвинцева Л.В., Добрынин В.Н., Мишин А.А. Интеллектуальное робастное управление: технологии мягких вычислений. М.: ВНИИгеосистем, 2011. 406 с.

2.     Grasser F., D’Arrigo A., Colombi S., and Rufer A. Joe: a mobile inverted pendulum. IEEE Transaction Electronics, 2002, vol. 49, no 1, pp. 107–114.

3.     Gpmez M., Arribas T., Sanchez S. Optimal control based on CACM-RL in a Two-Wheeled Inverted Pendulum. Intern. Journ. of Advanced Robot System, 2012.

4.     Jung S., Taek H. Cho. Decoupled Neural Network Refe­rence Compensation Technique for a PD Controlled Two Degrees-of-Freedom Inverted Pendulum. Intern. Journ. of Control, Automa­tion, and Systems, 2004, vol. 2, no. 1, pp. 92–99.

5.     Moghaddas M., RezaDastranj M., Changizi N., and Khoo- ri N. Design of Optimal PID Controller for Inverted Pendulum Using Genetic Algorithm. Intern. Journ. of Innovation, Manage­ment and Technology, 2012, vol. 3, no. 4.

6.     Kumar P., Mehrotra O.N., Mahto J. Tuning of PID con­troller of inverted pendulum using genetic algorithm. International Journal of Research in Engineering and Technology, 2012, vol. 01, iss. 03.

7.     Choi D., Oh J.-H. Human-friendly motion control of a wheeled inverted pendulum by reduced-orderdisturbance observer. IEEE Intern. Conf. on Robotics and Automation Pasadena, CA, USA, May 19–23, 2008, pp. 2521–2526.

8.     Nawawi S.W., Ahmad M.N., and Osman J.H.S. Real-time control system for a two-wheeled inverted pendulum mobile – robot. Advanced Knowledge Application in Practice, InTech, 2010, pp. 299–312.

9.     Gocmen A. Design of two wheeled electric vehicle. Master Sci. Thesis. Atilim Univ., Temmuz, 2011.

10.  Castro A. Modeling and dynamic analysis of a two-wheeled inverted pendulum. Master Sci. Thesis, Georgia Institute of Technology, Atlanta, USA, 2012.

11.  Ульянов С.В., Решетников А.Г. Метод извлечения знаний из физически измеряемого сигнала обучения: проектирование баз знаний нечеткого регулятора // Системный анализ в науке и образовании. 2013. № 1. URL: http://www.sanse.ru/archi­ve/154 (дата обращения: 16.09.2013).

12.  Ульянов С.В., Решетников А.Г., Керимов Т.А., Дистанционная настройка базы знаний для интеллектуального управления автономным роботом на основе оптимизатора баз знаний. Ч. 1: технологии мягких вычислений. 2013. № 1. URL: http://www.sanse.ru/archive/156 (дата обращения: 16.09.2013).

13.  Buonocunto P., Corucci F. Real-time PID control of an inverted pendulum. MSc in Computer Engineering, Univ. of Pisa, Italy.

References

1.     Ulyanov S.V., Litvintseva L.V., Dobrynin V.N., Mi- shin A.A. Intellektualnoe robastnoe upravlenie: tekhnologii myagkikh vychisleniy [Intellegent robust control: soft computing technolo­gies]. Moscow, VNIIgeosystem Publ., 2011, 406 p.

2.     Grasser F., D’Arrigo A., Colombi S., Rufer A. Joe: A mobile inverted pendulum, IEEE Transaction Electronics. 2002, vol. 49, no. 1, pp. 107–114.

3.     Gpmez M., Arribas T., Sanchez S. Optimal control based on CACM-RL in a Two-Wheeled Inverted Pendulum. Int. journ. of advanced robot system. 2012 (accessed 30 October 2012).

4.     Jung S., Cho T.H. Decoupled Neural Network Reference Compensation Technique for a PD Controlled Two Degrees-of-Freedom Inverted Pendulum. Int. journ. of control, automation, and systems. 2004, vol. 2, no. 1, pp. 92–99.

5.     Moghaddas M., RezaDastranj M., Changizi N., Khoori N. Design of Optimal PID Controller for Inverted Pendulum Using Genetic Algorithm. Int. journ. of innovation, management and tech­nology. 2012, vol. 3, no. 4.

6.     Kumar P., Mehrotra O.N., Mahto J., Tuning of PID con­troller of inverted pendulum using genetic algorithm. Int. journ. of research in engineering and technology. 2012, vol. 01, iss. 03. Available at: http://ijret.org/volumes/2012_11_Vol_01_Iss_03/ P2012_01_03_029.pdf (accessed 10 August).

7.     Choi D., Oh J.-H. Human-friendly motion control of a wheeled inverted pendulum by reduced-orderdisturbance observer. IEEE int. conf. on robotics and automation pasadena. CA, USA, 2008, pp. 2521–2526.

8.     Nawawi S.W., Ahmad M.N., Osman J.H.S. Real-time control system for a two-wheeled inverted pendulum mobile – robot. Advanced knowledge application in practice. 2010, pp. 299–312.

9.     Gocmen A. Design of two wheeled electric vehicle. Master Sc. thesis, Atilim Univ. Publ., Temmuz, 2011.

10.  Castro A. Modeling and dynamic analysis of a two-wheeled inverted pendulum. Master Sc. thesis, Georgia Institute of Technology Publ., Atlanta, USA, 2012.

11.  Ulyanov S.V., Reshetnikov A.G. Knoledge extract method from physically measured teaching signal: knowledge base design for fuzzy controller. Sistemny analiz v nauke i obrazovanii [System analyze in science and education]. Available at: http://www.san­se.ru/archive/154 (accessed 16 September 2013).

12.      Ulyanov S.V., Reshetnikov A.G., Kerimov T.A. Remote configuration of knowledge base for autonomous robot intelligent control based on knowledge base optimizer: soft conputing. Sistem­ny analiz v nauke i obrazovanii [System analyze in science and education]. Available at: http://www.sanse.ru/archive/156 (accessed 16 September 2013).

13.      Buonocunto P., Corucci F. Real-time PID control of an in­verted pendulum. MSc in Comp. Engineering, Univ. of Pisa, Italy.