К сложным распределенным системам относятся различные составляющие в виде физических, биологических и цифровых систем, для которых, как правило, существует опасность в виде внешних угроз, способствующих нанесению существенного материального ущерба (в том числе и целенаправленного воздействия на человека, а также прямого воздействия человека на объекты, создающие внешние угрозы). Например, в Республике Башкортостан одной из таких угроз является весенний паводок, ставящий под угрозу сложные распределенные системы из-за их возможного подтопления и затопления, поэтому задача прогнозирования паводковой ситуации важна и актуальна.
В связи с появлением новых технических возможностей автоматического измерения па-раметров состояния (уровня воды, темпера-туры, скорости и направления ветра и др.) сложных распределенных систем в последнее время все большее применение находят автоматические станции измерения и видеофиксации уровня воды в водных объектах [1–4]. Основное назначение этих станций – раннее обнаружение угрозы (паводка) и информирование о ней органов управления и населения [5, 6]. В то же время данные постов можно использовать для прогнозирования паводковой ситуации по предложенной в статье [7] методике.
В условиях отсутствия архивных измерений на автоматических постах (ранее они просто не существовали) предлагается ввести оценку уровня воды в точках размещения автоматических станций на основе архивных значений со-седних стационарных гидрологических постов. Причем уровень воды в этих точках находился на какой-то отметке и закономерность его (уровня) изменения такая же, как на стационарных гидрологических постах. Этот метод можно использовать только для тех автоматических постов, которые находятся между стационарными гидрологическими постами (один выше по течению, другой ниже), и для них интерполируется значение уровня воды. При этом необходимо учитывать, что на стационарных гидрологических постах ежедневно измеряется дискретно одно значение уровня воды в фиксированный момент времени (обычно в 8 часов утра по местному времени), а на автоматических постах уровень воды измеряется непрерывно. Таким образом, было бы корректным в качестве значения уровня воды на k-м гидрологическом посту на конкретную дату выбирать среднее из непрерывно измеренных значений за 10 минут (с 755 до 805) на дату измерения.
Постановка задачи
Одним из основных параметров возможного негативного воздействия паводковой ситуации на различные компоненты сложных распределенных систем является h – уровень воды в водных объектах, измеряющийся ежедневно на n стационарных гидрологических постах сотрудниками Башгидромета. Введем обозначения:  – значение уровня воды, измеренное на n-м гидрологическом посту на i-ю дату j-го года. Здесь
– значение уровня воды, измеренное на n-м гидрологическом посту на i-ю дату j-го года. Здесь  , где n – количество гидрологических постов, участвующих в расчетах на первом этапе краткосрочного прогнозирования уровней воды [8]; j – номер года; i – конкретная дата измерения.
, где n – количество гидрологических постов, участвующих в расчетах на первом этапе краткосрочного прогнозирования уровней воды [8]; j – номер года; i – конкретная дата измерения.
Далее вводим обозначение  – уровень воды водных объектов, измеряющийся ежедневно на na автоматических станциях в i-ю дату j-го года, где
– уровень воды водных объектов, измеряющийся ежедневно на na автоматических станциях в i-ю дату j-го года, где 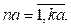 Задача краткосрочного прогнозирования уровней воды на автоматических станциях аналогична задаче краткосрочного прогнозирования на стационарных гидрологических постах и заключается в том, чтобы в конкретный текущий i-й день измерения вычислить значение уровня подъема воды на следующий i + 1-й день, то есть
Задача краткосрочного прогнозирования уровней воды на автоматических станциях аналогична задаче краткосрочного прогнозирования на стационарных гидрологических постах и заключается в том, чтобы в конкретный текущий i-й день измерения вычислить значение уровня подъема воды на следующий i + 1-й день, то есть  для любого
для любого  . Но при этом также одной из важнейших задач в рамках как краткосрочного, так и заблаговременного прогнозирования павод-ковой ситуации является восстановление исторических данных для расчета значения уровня воды на необходимые дату и год. Соответственно, для дальнейших расчетов введем обозначения:
. Но при этом также одной из важнейших задач в рамках как краткосрочного, так и заблаговременного прогнозирования павод-ковой ситуации является восстановление исторических данных для расчета значения уровня воды на необходимые дату и год. Соответственно, для дальнейших расчетов введем обозначения:  – восстанавливаемое значение уровня воды в месте размещения na-й автоматической станции на i-ю дату j-го года; kdn – нижестоящий по течению реки гидрологический пост; kun – вышестоящий по течению реки гидрологический пост. Здесь
– восстанавливаемое значение уровня воды в месте размещения na-й автоматической станции на i-ю дату j-го года; kdn – нижестоящий по течению реки гидрологический пост; kun – вышестоящий по течению реки гидрологический пост. Здесь  и
и  , где ka – количество автоматических станций контроля и мониторинга уровня воды, участвующих в расчетах; j – номер года; i – конкретная дата измерения; k – количество стационарных гидрологических постов. В рамках прогнозирования паводковой ситуации задача восстановления исторических значений уровней воды состоит в том, чтобы в конкретный i-й день измерения интерполировать значение уровня подъема воды на автоматической станции, находящейся между kdk и kuk.
, где ka – количество автоматических станций контроля и мониторинга уровня воды, участвующих в расчетах; j – номер года; i – конкретная дата измерения; k – количество стационарных гидрологических постов. В рамках прогнозирования паводковой ситуации задача восстановления исторических значений уровней воды состоит в том, чтобы в конкретный i-й день измерения интерполировать значение уровня подъема воды на автоматической станции, находящейся между kdk и kuk.
Использование данных автоматических станций для прогнозирования уровней воды

 Как отмечалось ранее, задача восстановления исторических данных является важной и актуальной из-за отсутствия необходимой информации для прогнозирования уровней воды на автоматических станциях. Изначально для восстановления необходимых данных для прогнозирования уровней воды на автоматических станциях является важным определение их географического расположения на определенной территории в рамках сложной распределенной системы. На рисунке 1 показано расположение стационарных гидрологических постов (34 объекта) и автоматических постов (38 объектов) на водных объектах Республики Башкортостан. Анализ их взаимного расположения (рис. 1) показал, что 7 автоматических постов (во время паводка 2020 г.) находятся между стационарными гидрологическими постами (табл. 1).
Как отмечалось ранее, задача восстановления исторических данных является важной и актуальной из-за отсутствия необходимой информации для прогнозирования уровней воды на автоматических станциях. Изначально для восстановления необходимых данных для прогнозирования уровней воды на автоматических станциях является важным определение их географического расположения на определенной территории в рамках сложной распределенной системы. На рисунке 1 показано расположение стационарных гидрологических постов (34 объекта) и автоматических постов (38 объектов) на водных объектах Республики Башкортостан. Анализ их взаимного расположения (рис. 1) показал, что 7 автоматических постов (во время паводка 2020 г.) находятся между стационарными гидрологическими постами (табл. 1).
Обозначим общее количество автоматических станций, расположенных между двумя стационарными постами, через na. На сегодняшний день na = 7, но со временем автоматические станции могут закрываться, перемещаться на другое место или ликвидироваться, поэтому na является переменной величиной. Соответственно, обозначим  как интерполированное оценочное значение уровня воды в месте размещения na-й автоматической станции,
как интерполированное оценочное значение уровня воды в месте размещения na-й автоматической станции,  в i-й день j-го года. Через KD обозначим множество номеров стационарных гидрологических постов, расположенных ниже по течению, а через KU – множество номеров стационарных гидрологических постов, расположенных выше по течению соответствующей автоматической станции так, что
в i-й день j-го года. Через KD обозначим множество номеров стационарных гидрологических постов, расположенных ниже по течению, а через KU – множество номеров стационарных гидрологических постов, расположенных выше по течению соответствующей автоматической станции так, что
KD = (kd1, kd2, …, kdna),
KU = (ku1, ku2, …, kuna), (1)
автоматическая станция с номером na находится между двумя стационарными гидрологическими постами с номерами kdn и kun.
В расчетах (интерполяции) значения  участвует расстояние между автоматической станцией и соседними стационарными гидрологическими постами, поэтому введем в рассмотрение переменную x, которая обозначает расстояние (удаление) соответствующего поста от устья реки, и, вообще говоря, уровень воды в любой точке реки можно рассматривать как функцию от этого расстояния:
участвует расстояние между автоматической станцией и соседними стационарными гидрологическими постами, поэтому введем в рассмотрение переменную x, которая обозначает расстояние (удаление) соответствующего поста от устья реки, и, вообще говоря, уровень воды в любой точке реки можно рассматривать как функцию от этого расстояния:
h = h(x). (2)
Для каждого n-го стационарного поста это расстояние есть фиксированное число xn,  ; соответственно, для автоматических станций обозначим его xana,
; соответственно, для автоматических станций обозначим его xana,  . Используя введенные обозначения, нахождение некоторого автоматического поста между двумя стационарными гидрологическими постами опишем соотношением
. Используя введенные обозначения, нахождение некоторого автоматического поста между двумя стационарными гидрологическими постами опишем соотношением
 (3)
(3)
В общем случае эта зависимость имеет одну и ту же природу, определяемую соотношением (2), но для пояснения алгоритма интерполяции для стационарных гидрологических постов и автоматических станций вводятся отличающиеся друг от друга обозначения.
Предполагая, что изменение уровня воды в реке между двумя точками (местами расположения гидрологических постов) происходит линейно (это для небольших расстояний вполне приемлемо), интерполируемое значение  находится на прямой линии, соединяющей точки уровня воды на соседних стационарных постах, и вычисляется (в соответствии с известными правилами Евклидовой геометрии, см. рис. 2) по соотношению
находится на прямой линии, соединяющей точки уровня воды на соседних стационарных постах, и вычисляется (в соответствии с известными правилами Евклидовой геометрии, см. рис. 2) по соотношению
 . (4)
. (4)

 На рисунке 3 показан пример полученных в результате интерполяции значений уровня подъема воды для автоматической станции «Красный Ключ» на основе данных соседних стационарных гидрологических постов – «с. Красная Горка (р. Уфа)» и «Павловская ГЭС, нижний бьеф (р. Уфа)». В качестве примера используются исторические данные уровней воды на данных гидрологических постах от 04.05.2009 г.: уровень воды на посту «с. Крас-ная Горка (р. Уфа)» составил 197 см, на посту «Павловская ГЭС, нижний бьеф (р. Уфа)» – 413 см. В результате интерполяции для автоматического поста «Красный Ключ» получено значение уровня воды – 223 см, которое будем считать историческим показателем для этого автоматического поста на 04.05.2009 г. Таким образом, полученные в результате интерполяции значения уровня воды для каждого автоматического поста и на все остальные даты будем считать историческими данными для этого автоматического поста. Количество этих данных соответствует количеству наблюдений на соседних стационарных гидрологических постах.
На рисунке 3 показан пример полученных в результате интерполяции значений уровня подъема воды для автоматической станции «Красный Ключ» на основе данных соседних стационарных гидрологических постов – «с. Красная Горка (р. Уфа)» и «Павловская ГЭС, нижний бьеф (р. Уфа)». В качестве примера используются исторические данные уровней воды на данных гидрологических постах от 04.05.2009 г.: уровень воды на посту «с. Крас-ная Горка (р. Уфа)» составил 197 см, на посту «Павловская ГЭС, нижний бьеф (р. Уфа)» – 413 см. В результате интерполяции для автоматического поста «Красный Ключ» получено значение уровня воды – 223 см, которое будем считать историческим показателем для этого автоматического поста на 04.05.2009 г. Таким образом, полученные в результате интерполяции значения уровня воды для каждого автоматического поста и на все остальные даты будем считать историческими данными для этого автоматического поста. Количество этих данных соответствует количеству наблюдений на соседних стационарных гидрологических постах.
Теперь массив полученных оценочных данных можно использовать для прогноза уровней воды по предложенному в статьях [7, 8] методу с применением рекуррентной искусственной нейронной сети второго поколения (используются структура в виде одного входного, трех промежуточных (скрытых) и одного выходного слоев, а также сигмоидальная функция активации и обучение без учителя на основе интеграции методов обратного распространения ошибки и Розенблатта (более подробное описание представлено в [8])) для всех автоматических постов, входящих в таблицу 1.
Анализ эффективности предлагаемого метода восстановления данных
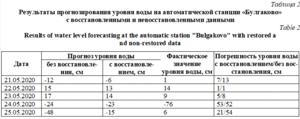 В качестве примера эксперимент (табл. 2) проводился на большом количестве данных (объем выборки – 8 860 значений, при этом общий размер данных, используемых для анализа по всем гидропостам и автоматическим станциям на территории Республики Башкортостан, – более 500 Гб) в рамках паводка 2020 г., измеряемых на стационарных гидрологических постах мониторинга уровней воды («Ляхово» и «Охлебинино», между которыми находится автоматическая станция «Булгаково»), подведомственных Башкирскому управлению по гидрометеорологии и мониторингу окружающей среды.
В качестве примера эксперимент (табл. 2) проводился на большом количестве данных (объем выборки – 8 860 значений, при этом общий размер данных, используемых для анализа по всем гидропостам и автоматическим станциям на территории Республики Башкортостан, – более 500 Гб) в рамках паводка 2020 г., измеряемых на стационарных гидрологических постах мониторинга уровней воды («Ляхово» и «Охлебинино», между которыми находится автоматическая станция «Булгаково»), подведомственных Башкирскому управлению по гидрометеорологии и мониторингу окружающей среды.
Суть эксперимента заключается в прогнозировании уровня воды на одни сутки с восста-новленными данными по представленному методу и без интерполируемых значений. С момента начала наблюдения ежедневно за раз-витием паводковой ситуации (в 2020 г. – 18 апреля) с помощью программы Forecaster, реализованной на основе свободно распространяемой библиотеки машинного обучения TensorFlow версии 2.3.0 [9], осуществлялся прогноз на следующий день по одной автоматической станции. На следующий день измерялся фактический уровень воды на этом же посту.
Таким образом, в ходе эксперимента была доказана целесообразность использования восстановления данных на автоматической станции с последующим применением интерполированных значений (4) в рамках прогнозирования паводковой ситуации за счет увеличения точности прогноза.
Заключение
В данной статье предложен метод прогно-зирования паводковой ситуации на основе восстановления исторических данных на автоматических станциях, расположенных между вышестоящими и нижестоящими гидрологическими постами, что позволяет использовать дополнительные данные об уровнях воды для прогнозирования паводковой ситуации. Анализ результатов применения предложенного метода восстановления данных на автоматических станциях для прогнозирования уровня воды во время паводковой ситуации 2020 г. в Республике Башкортостан показал его эффективность. Был получен более точный прогноз в отличие от прогнозирования без восстановления данных. Таким образом, использование предлагаемого метода позволит более точно прогнозировать уровень воды на автоматиче-ских станциях контроля и мониторинга уровня воды, что даст возможность соответствующим службам оперативно реагировать на угрозу па-водка и принимать необходимые меры для ее парирования.
Исследование выполнено при финансовой поддержке РФФИ, проект № 20-08-00301.
Литература
1. Белюченко И.С. Региональный мониторинг – научная основа сохранения природы. Экологический вестник Северного Кавказа. 2006. Т. 2. № 1. С. 25–40.
2. Матишов Г.Г., Чикин А.Л., Бердников С.В., Шевердяев И.В., Клещенков А.В., Кириллова Е.Э. Экстремальное затопление дельты Дона весной 2013 г.: хронология, условия формирования и последствия // Вестн. ЮНЦ РАН. 2014. Т. 10. № 1. С. 17–24.
3. Никитин О.П., Поснов А.А. Измерения уровня моря в неблагоприятных условиях окружающей среды // Океанологические исследования. 2018. Т. 46. № 1. С. 128–133. DOI: 10.29006/1564-2291.jor-2018.46(1).11.
4. Гундров Д.С. Автоматизированная система мониторинга и прогнозирования паводковой обстановки на водных объектах Краснодарского края и перспективы ее развития // Пожарная безопасность: проблемы и перспективы. 2019. С. 200–202.
5. Moghar A., Hamiche M. Stock market prediction using LSTM recurrent neural network. Procedia Computer Science, 2020, vol. 170, pp. 1168–1173. DOI: 10.1016/j.procs.2020.03.049.
6. Mokhov V.G., Tsimbol V.I. Electrical energy consumption prediction of the federal district of Russia on the based of the reccurent neural network. J. Comp. Eng. Math., 2018, vol. 5, no. 2, pp. 3–15. DOI: 10.14529/jcem180201.
7. Palchevsky E.V., Khristodulo O.I., Pavlov S.V. Threats complex distributed systems parrying based on their development prognostication. Proc. VIII Sci. Conf. ITIDS, 2020, pp. 191–194. DOI: 10.2991/aisr.k.201029.036.
8. Пальчевский Е.В., Христодуло О.И., Павлов С.В., Соколова А.В. Анализ ретроспективных данных с применением технологий искусственного интеллекта для прогнозирования угроз в сложных распределенных системах // Вестн. компьютерных и информационных технологий. 2021. T. 18. № 2. С. 39–45. DOI: 10.14489/vkit.2021.02.pp.039-045.
9. Пальчевский Е.В. Обучаемая с учителем нейронная сеть для прогнозирования уровня воды на гидропостах: Свид. о регистр. ПрЭВМ № 2020611923. Рос. Федерация, 2020.
References
- Belyuchenko I.S. Regional monitoring as the scientific basis of nature preservation. The North Caucasus Ecological Herald, 2006, vol. 2, no. 1, pp. 25–40 (in Russ.).
- Matishov G.G., Chikin A.L., Berdnikov S.V., Sheverdyaev I.V., Kleshchenkov A.V., Kirillova E.E. Extreme flooding of the Don delta in spring 2013: Chronology, conditions of formation and consequences. Vestn. Juzhnogo Nauchnogo Centra RAS, 2014, vol. 10, no. 1, pp. 17–24 (in Russ.).
- Nikitin O.P., Posnov A.A. Sea-level measurements in hostile conditions. Journal of Oceanological Research, 2018, vol. 46, no. 1, pp. 128–133. DOI: 10.29006/1564-2291.jor-2018.46(1).11 (in Russ.).
- Gundrov D.S. Flood monitoring and forecasting automated systems of water enviroment of the krasnodar region, development prospects. Pozharnaja Bezopasnost': Problemy i Perspektivy, 2019,
pp. 200–202 (in Russ.).
- Moghar A., Hamiche M. Stock market prediction using LSTM recurrent neural network. Procedia Computer Science, 2020, vol. 170, pp. 1168–1173. DOI: 10.1016/j.procs.2020.03.049.
- Mokhov V.G., Tsimbol V.I. Electrical energy consumption prediction of the federal district of Russia on the based of the reccurent neural network. J. Comp. Eng. Math., 2018, vol. 5, no. 2, pp. 3–15. DOI: 10.
14529/jcem180201.
- Palchevsky E.V., Khristodulo O.I., Pavlov S.V. Threats complex distributed systems parrying based on their development prognostication. Proc. VIII Sci. Conf. ITIDS, 2020, pp. 191–194. DOI: 10.2991/aisr.k.
201029.036.
- Palchevsky E.V., Khristodulo O.I., Pavlov S.V., Sokolova A.V. Analysis of historical data using artificial intelligence technologies for predicting threats in complex distributed systems. Vestn. Komp'iuternykh i Informatsionnykh Tekhnologii, 2021, vol. 18, no. 2, pp. 39–45. DOI: 10.14489/vkit.2021.02.pp.039-045 (in Russ.).
- Palchevsky E.V. Supervised Neural Network for Predicting Water Level at Gauging Stations. Patent RF, no. 2020611923, 2020.


 (3)
(3)


