Journal influence
Bookmark
Next issue
Integration of reinforcement learning methods and fuzzy logic for intelligent real-time systems
Abstract:The paper considers the possibilities of integrating reinforcement learning methods and fuzzy logic in terms of improving the efficiency of reinforcement learning algorithms. The main focus is on applying such integrated methods in real-time intelligent systems, especially in decision support systems for monitoring and controlling complex technical objects. The basis is a reinforcement learning method based on temporal differences; an environmental state and the reward signal are formed using fuzzy logic. The paper presents software implementation and the data of computer simulation of deep learning methods with reinforcement based on temporal differences obtained from a comparative analysis of a fuzzy logic algorithm and neural network algorithms. The authors of the paper show that the main advantages of reinforcement learning algorithms using fuzzy logic are: training effectiveness in terms of minimizing the number of episodes, which is especially important regarding the availability of limited data for training or rapid adaptation of real-time training; resistance to noise and outliers in data, which is important in real environments with noise or data changes; interpretability - fuzzy logic algorithms provide interpretable rules and conclusions based on fuzzy logic; extension of a reinforcement learning scope to subject/problem areas and tasks with a continuous state space. These researches and developments are carried out in terms of designing intelligent real-time decision support systems. Such systems are designed to help operational dispatch personnel (decision makers) in monitoring and managing complex technical and organizational systems under fairly severe time constraints and various types of uncertainties (inaccuracies, fuzziness, inconsistencies) in the information entering a system, i.e. in the presence of so-called noisy data.
Аннотация:В данной работе рассмотрены возможности интеграции методов обучения с подкреплением и нечеткой логики в плане повышения эффективности алгоритмов обучения с подкреплением. Главное внимание уделяется применению таких интегрированных методов в интеллектуальных системах реального времени, особенно в системах поддержки принятия решений для мониторинга и управления сложными техническими объектами. Как основа используется метод обучения с подкреплением на базе темпоральных различий, состояние среды и сигнал вознаграждения формируются с применением нечеткой логики. Представлена программная реализация и приводятся данные компьютерного моделирования методов глубокого обучения с подкреплением на основе темпоральных различий, полученные при сравнительном анализе алгоритма на основе нечеткой логики и алгоритмов на основе нейронных сетей. Показано, что основными достоинствами алгоритмов обучения с подкреплением с применением нечеткой логики являются: эффективность обучения, выражающаяся в минимизации количества эпизодов, что особенно важно, когда доступность данных для обучения ограничена или обучение в реальном времени требует быстрой адаптации; устойчивость к шуму и выбросам в данных, что важно в реальных средах, где присутствуют шумы или изменяются данные; интерпретируемость – алгоритмы с нечеткой логикой предоставляют интерпретируемые правила и выводы на основе нечеткой логики; расширение области применения обучения с подкреплением на предметные/проблемные области и задачи с непрерывным пространством состояний. Данные исследования и разработки выполняются в рамках конструирования интеллектуальных систем поддержки принятия решений реального времени. Эти системы предназначены для помощи оперативно-диспетчерскому персоналу (лицам, принимающим решения) при мониторинге и управлении сложными техническими и организационными системами в условиях достаточно жестких временных ограничений и при наличии различного типа неопределенностей (неточности, нечеткости, противоречивости) в поступающей в систему информации, то есть так называемых зашумленных данных.
| Authors: Eremeev, A.P. (eremeev@appmat.ru) - National Research University “MPEI” (Professor), Moscow, Russia, Ph.D, Sergeev, M.D. (SergeevMD@mpei.ru) - National research University "MPEI" (Postgraduate Student), Moscow, Russia, Petrov, V.S. (PetrovVS@mpei.ru) - National research University "MPEI" (Student), Moscow, Russia | |
| Keywords: decision support, real time, intellectual system, fuzzy logic, time, reinforcem ent learnin, artificial intelligence |
|
| Page views: 1299 |
PDF version article |
Введение. Возможности создания интегрированной среды, объединяющей методы обучения с подкреплением (reinforcement learning, RL), гибкие алгоритмы поиска решения (anytime algorithms) и мультиагентный подход, а также применение БД NO-SQL уже были рассмотрены в [1, 2]. Выявлена перспективность интеграции в интеллектуальные системы поддержки принятия решений реального времени (ИСППР РВ), ориентированных на динамические предметные/проблемные области, искусственных нейронных сетей (ИНС) и RL-обу- чения на основе временных (темпоральных) различий (temporal differences, TD). Основные положения RL-обучения изложены в [3]. В данной работе показаны возможности применения нечеткой логики в методах обучения с подкреплением, представлены разработка соответствующих программных средств и результаты компьютерного моделирования на ряде типовых задач. RL-обучение с учетом временных различий: эффективный подход к обучению с подкреплением В работе [1] продемонстрировано, что одним из наиболее эффективных подходов к обучению с подкреплением в ИСППР РВ с учетом критерия «временные затраты–качество обучения» является RL-обучение на основе темпоральных различий (TD-обучение). Процесс обучения основан на опыте, полученном при взаимодействии агента с окружающей средой без необходимости предварительного знания о ней. Разработанные для многомерных временных рядов TD-методы обладают способностью обновлять расчетные оценки без ожидания окончательного результата, что делает их самонастраиваемыми. Особенно полезны они в динамических предметных областях и ИСППР РВ семиотического типа. Такие системы способны адаптироваться и подстраиваться к из- менениям в управляемом объекте и окружающей среде [1, 4]. В наиболее простом TD-методе TD(0) функция ценности (оценка) рассчитывается по следующей формуле:
где Vst – оценка функции ценности нетерминального состояния st в момент времени t; rt + 1 – полученное вознаграждение на текущем шаге; α – длина шага; γ – ценность терминального состояния. Важно отметить, что TD-методы дают свои оценки, частично основываясь на предыдущих, что позволяет им самонастраиваться. Преимущества TD-методов в том, что они не требуют знания модели окружающей среды, включая вознаграждения и вероятностное распределение последующих состояний, а также могут оценивать выгоду уже на следующем временном шаге, не ожидая завершения всего эпизода. Даже в случае длительных эпизодов процесс обучения не замедляется. Известно, что TD-алгоритм для любой заданной стратегии π сходится к функции V в среднем при использовании постоянного шага и в пределе сходится с вероятностью 1, если длина шага уменьшается в соответствии с условиями стохастической аппроксимации:
В работе [4] показано, что одним из важнейших достижений в области обучения с подкреплением является развитие управления с использованием TD-метода с разделенной оценкой ценности стратегий, известного как Q-обучение [5, 6]. Простейшая форма этого подхода, известная как одношаговое Q-обучение, определяется как
где Q(st, at) – оценка функции ценности после перехода из нетерминального состояния s при действии a в момент времени t. Если состояние st + 1 является терминальным, значение Q(st + 1, at + 1) полагается равным нулю. Схема алгоритма Q-обучения имеет следующий вид: Инициализировать Q(s, a) произвольно Повторять (для каждого эпизода): Инициализировать s Повторять (для каждого шага эпизода): Найти а по s, используя стратегию, полученную из Q (например, ε-жадную) Выполнить действие а, найти r, s¢
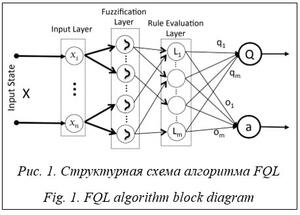
s ¬ s¢ Пока s не станет завершающим состоянием Недостатком данного подхода является необходимость дискретизировать все возможные пары «состояние–действие» и анализировать их многократно для нахождения оптимальных значений функции ценности. Чтобы решить эту проблему, предлагается использовать нечеткую логику для моделирования состояний и функции вознаграждения. Обучение с подкреплением с применением нечеткой логики Нечеткое Q-обучение (fuzzy Q-learning, FQL) – это расширение алгоритма Q-обучения, позволяющее преодолеть упомянутую выше проблему [7]. Кроме того, FQL позволяет инкапсулировать экспертные знания в систему, ускоряя процесс обучения. В FQL принятие решений представлено системой нечеткого логического вывода (fuzzy inference system, FIS), которая рассматривает большие дискретные или непрерывные состояния как входные данные. Идея алгоритма FQL заключается в использовании так называемой q-таблицы в качестве компактной версии Q-таблицы для представления обучающих данных. В FQL система логического вывода описана набором правил J, где j Î J определяется как IF(x1 is Lj1)…AND (xn is Ljn)… AND (xN is LjN) THEN a = oj with q(Lj, oj), где Ljn – метка входной переменной xn, x – вектор состояния, x = [x1, …, xn, …, xN], участвующий в j-правиле; oj = [oj1,…, ojk,…, ojK] – выходное множество действий для правила j, каждому из которых соответствует вектор Lj = [Lj1, …, Ljn,…, LjN]. Значение Q(Lj, ojk) называется значением q-функции в состоянии Lj и действии ojk j-го правила.
Алгоритм FQL имеет двухуровневый выбор действия. На первом уровне (уровень локальных действий) набор действий выбирается в соответствии со стратегией разведки/применения. Такая стратегия позволяет агенту исследовать неопробованные действия, чтобы получить больше опыта, и сочетать это с использованием уже известных успешных действий для обеспечения высокого долгосрочного вознаграждения. В реализации алгоритма используется ε-жадный метод в качестве стратегии для экспериментов. В этом методе на каждом временном шаге агент выбирает случайное действие с фиксированной вероятностью 1 – ε, где ε обычно берется близким к 1. С вероятностью ε действие выбирается жадно из изученных оптимальных действий по отношению к q-таблице с вероятностью
где ojl – выбранное локальное действие j-го правила. На втором уровне выбора действия (выбор предполагаемого действия) назначенное действие для входного вектора x выбирается из набора локальных действий следующим образом:
Чтобы подчеркнуть временную зависимость, в уравнение добавляется индекс времени. Аппроксимация значения качества состояния xt вычисляется на основе уравнения
После выполнения действия a система переходит в следующее состояние xt + 1, агент получает вознаграждение rt + 1. Для входного вектора xt+1 вычисляется значение Value-функции состояния:
Учитывая приведенные выше уравнения, вычисляется TD-ошибка:
где γ – дисконтирующий множитель. Обновление q-функции для каждого активного правила j Î Jx выглядит следующим образом:
Компьютерное моделирование Сравнение эффективности RL-обучения на основе темпоральных различий с применением нечеткой логики проводилось с описанными в [2] методами RL-обучения. С применением ИНС DQN, DDQN и AC (Actor-Critic) были реализованы и испытаны соответствующие алгоритмы глубокого RL-обучения [2, 9, 10]. Для тести- рования методов выбраны хорошо известные задачи, такие как перевернутый маятник (CartPole) и задача о горном автомобиле (Mountain Car).
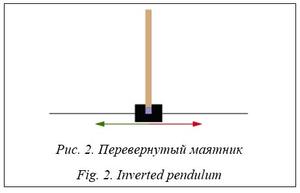
Среда задается состоянием, действием, наградой, начальным состоянием и флагом завершения эпизода. Состояние описывается следующими величинами: - позиция тележки – значение в диапазоне [-4.8, 4.8]; - скорость тележки; - угол отклонения шеста от вертикали – значение в диапазоне [-24°, 24°], (-0.204, 0.204) в радианах; - скорость изменения угла наклона шеста. Действие может принимать значения 0 и 1: 0 – толкнуть тележку влево (приложить к ней горизонтальную силу, равную +1); 1 – толкнуть тележку вправо (приложить к ней горизонтальную силу, равную -1). Награда на каждом шаге равна 1, при падении стержня – награда -1. Начальное состояние задается как [0,0,0,0]. Случаи завершения эпизода: - угол шеста вышел из диапазона [-12°, 12°]; - позиция тележки вышла из допустимого диапазона [-2.4, 2.4]; - длина эпизода >500.
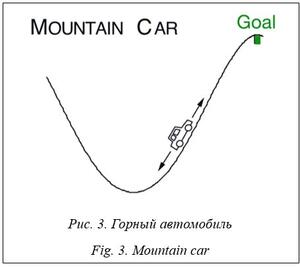
Среда MountainCar описывается рядом компонентов. Состояние среды определяется двумя величинами: - позиция автомобиля: это значение указывает положение автомобиля на горизонтальной оси (диапазон значения – от -1.2 до 0.6); - скорость автомобиля: это скорость движения автомобиля по горизонтальной оси (диапазон значения – от -0.07 до 0.07). Агент может выбирать одно из трех действий: - двигаться влево: автомобиль будет приме- нять газ и двигаться влево; - ничего не делать: автомобиль не изменяет скорость; - двигаться вправо: автомобиль будет при- менять газ и двигаться вправо. Награда: на каждом шаге агент получает награду -1. Цель агента – въехать на вершину горы, по достижении вершины горы агент получает награду 0. Достижение вершины горы считается успешным завершением задачи. Начальное состояние задается следующим образом: позиция автомобиля – случайное значение из интервала [-0.6, -0.4], скорость автомобиля – 0. Случаи завершения эпизода: - достигнута вершина горы – позиция автомобиля >0.5; - длина эпизода >200. Был реализован алгоритм Q-обучения с нечеткой логикой (FQL). Для сравнительного анализа использовались DRL-методы DQN, DDQN и AC, реализованные в [8]. Приведем нечеткие правила для задач CartPole и MountainCar. Нечеткие правила для задачи перевернутого маятника:
Нечеткие правила для задачи горного автомобиля:
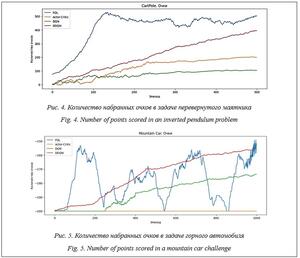
Из графика на рисунке 4 можно сделать вывод, что алгоритм с применением нечеткой ло- гики FQL лучше справляется с задачей перевернутого маятника, чем DRL-методы DQN, DDQN и AC, которые также показывают достаточно высокую эффективность. Нечеткая логика позволила за довольно малое число эпизодов (127) достичь высокой награды в 497 очков (максимально возможная награда 500 очков). На рисунке 5 представлены графики зависимости среднего вознаграждения от номера эпизода в задаче горного автомобиля. Для этой задачи алгоритм FQL за малое число эпизодов (116) достиг награды -155, в то время как алгоритму DDQN потребовалась 1 000 эпизодов для достижения награды -158, а алгоритм AC не справился с задачей. Однако в некоторых эпизодах FQL не смог справиться с задачей (например, при награде -200), что указывает на недостаточное описание системы нечеткими правилами. Изменение набора нечетких правил позволяет улучшить результаты. Реализация алгоритмов выполнена в среде Google Collab с использованием Python 3.10. Заключение В статье рассмотрен метод RL-обучения на основе TD-методов с применением нечеткой логики. Проведен сравнительный анализ алгоритма глубокого обучения с подкреплением с применением нечеткой логики FQL с алгоритмами на основе DRL-методов DQN, DDQN и AC. Проанализированы результаты работы методов обучения с подкреплением с применением нечеткой логики при компьютерных испытаниях реализованных на их основе алгоритмов обучения. Можно отметить основные достоинства алгоритмов обучения с подкреплением с применением нечеткой логики. Эффективность обучения: такие алгоритмы требуют меньшего количества эпизодов, поскольку обобщают знания из небольшого набора обучающих примеров. Это особенно важно, когда доступность данных для обучения ограничена или обучение в реальном времени требует быстрой адаптации. Устойчивость к шуму: алгоритмы устойчивы к шуму и выбросам в данных, поскольку нечеткая логика учитывает их вариации и осуществляет обработку более гибко. Это важно в реальных средах, где существуют шумы или изменения в данных. Интерпретируемость: алгоритмы с нечеткой логикой предоставляют интерпретируемые правила и выводы на основе нечеткой логики. Алгоритм позволяет понять, какие правила и механизмы лежат в основе принятия решений моделью. Кроме того, расширяется область применения Q-обучения: нечеткая логика позволяет использовать его для задач с непрерывным пространством состояний. В настоящее время рассматривается возможность интеграции методов RL-обучения (на основе Q- и TD-методов) с нейронными сетями в плане как использования RL-обучения для формирования обучающей выборки для нейронных сетей глубокого обучения, так и применения нейронных сетей при построении функций активации для Q-обучения. Список литературы 1. Еремеев А.П., Кожухов А.А. Реализация методов обучения с подкреплением на основе темпоральных различий и мультиагентного подхода для интеллектуальных систем реального времени // Программные продукты и системы. 2017. Т. 30. № 1. С. 28–33. doi: 10.15827/0236-235X.117.028-033. 2. Еремеев А.П., Сергеев М.Д. Интеграция методов обучения с подкреплением и искусственных нейронных сетей // Международный научно-технический конгресс ИС & ИТ-2022: тр. конгресса. 2022. С. 10–21. 3. Саттон Р.С., Барто Э.Г. Обучение с подкреплением; [пер. с англ]. М.: ДМК Пресс, 2020. 552 c. 4. Осипов Г.С. Методы искусственного интеллекта. М.: Физматлит, 2011. 296 с. 5. Chen Z., Deng S., Chen X., Li C., Sanchez R.-V., Qin H. Deep neural networks-based rolling bearing fault diagnosis. Microelectronics Reliability, 2017, vol. 75, pp. 327–333. doi: 10.1016/j.microrel.2017.03.006. 6. Hsu C.-C., Lin C.-W. CNN-based joint clustering and representation learning with feature drift compensation for large-scale image data. IEEE Transactions on Multimedia, 2017, vol. 20, no. 2, pp. 421–429. doi: 10.1109/TMM.2017.2745702. 7. Glorennec P.Y., Jouffe L. Fuzzy q-learning. Proc. Int. Fuzzy Systems Conf., 1997, vol. 2, pp. 659–662. doi: 10.1109/FUZZY.1997.622790. 8. Masoumzadeh S.S., Hlavacs H., Tomás L. A self-adaptive performance-aware capacity controller in overbooked datacenters. Proc. ICCAC, 2016, pp. 183–195. doi: 10.1109/ICCAC.2016.8. 9. François-Lavet V., Henderson P., Islam R., Bellemare M.G., Pineau J. An introduction to deep reinforcement learning. Foundations and Trends in Machine Learning, 2018, vol. 11, no. 3-4, pp. 219–354. doi: 10.1561/2200000071. 10. Mnih V., Kavukcuoglu K., Silver D., Rusu A.A., Veness J., Bellemare M.G. et al. Human-level control through deep reinforcement learning. Nature, 2015, vol. 518, no. 7540, pp. 529–533. doi: 10.1038/nature14236. References 1. Eremeev, A.P., Kozhukhov, A.A. (2017) ‘Implementation of reinforcement learning methods based on temporal differences and a multi-agent approach for real-time intelligent systems’, Software & Systems, 30(1), pp. 28–33 (in Russ.). doi: 10.15827/0236-235X.117.028-033. 2. Eremeev, A.P., Sergeev, M.D. (2022) ‘Integration of training methods with reinforcement and artificial neural networks’, Proc. Int. Congress "IS & IT-2022", pp. 10–21 (in Russ.). 3. Sutton, R.S., Barto, A.G. (2018) Reinforcement Learning. MA, Cambridge: The MIT Press, 552 p. (Russ. ed.: Moscow, 2020, 552 p.). 4. Osipov, G.S. (2015) Methods of Artificial Intelligence. Moscow, 296 p (in Russ.). 5. Chen, Z., Deng, S., Chen, X., Li, C., Sanchez, R.-V., Qin, H. (2017) ‘Deep neural networks-based rolling bearing fault diagnosis’, Microelectronics Reliability, 75, pp. 327–333. doi: 10.1016/j.microrel.2017.03.006. 6. Hsu, C.-C., Lin, C.-W. (2017) ‘CNN-based joint clustering and representation learning with feature drift compensation for large-scale image data’, IEEE Transactions on Multimedia, 20 (2), pp. 421–429. doi: 10.1109/TMM.2017.2745702. 7. Glorennec, P.Y., Jouffe, L. (1997) ‘Fuzzy q-learning’, Proc. Int. Fuzzy Systems Conf., 2, pp. 659–662. doi: 10.1109/FUZZY.1997.622790. 8. Masoumzadeh, S.S., Hlavacs, H., Tomás, L. (2016) ‘A self-adaptive performance-aware capacity controller in overbooked datacenters’, Proc. ICCAC, pp. 183–195. doi: 10.1109/ICCAC.2016.8. 9. François-Lavet, V., Henderson, P., Islam, R., Bellemare, M.G., Pineau, J. (2018) ‘An introduction to deep reinforcement learning’, Foundations and Trends in Machine Learning, 11(3-4), pp. 219–354. doi: 10.1561/2200000071. 10. Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A.A., Veness, J., Bellemare, M.G. et al. (2015) ‘Human-level control through deep reinforcement learning’, Nature, 518 (7540), pp. 529–533. doi: 10.1038/nature14236. | ||||||||||||||||||||||||
| Permanent link: http://swsys.ru/index.php?page=article&id=5038&lang=en |
Print version |
| The article was published in issue no. № 4, 2023 [ pp. 600-606 ] |
Perhaps, you might be interested in the following articles of similar topics:
- О реализации средств машинного обучения в интеллектуальных системах реального времени
- Реализация методов обучения с подкреплением на основе темпоральных различий и мультиагентного подхода для интеллектуальных систем реального времени
- Задачи построения интеллектуальной информационной системы управления безопасностью дорожного движения
- Программные средства поддержки принятия решений на основе нечетких табличных моделей представления знаний
- Построение онтологии на основе нереляционной базы данных для интеллектуальной системы поддержки принятия решений медицинского назначения
Back to the list of articles