Software & Systems

Усилия разработчиков космических аппаратов сегодня сосредоточены на повышении эффективности использования существующих космических систем и совершенствовании разработки и проектирования новых. Одним из способов достижения этих целей является рациональный выбор эффективных вариантов разрабатываемых систем, который требует применения адекватных моделей, эффективных алгоритмических средств и мощных компьютеров.

Одна из самых сложных и недостаточно изученных проблем – синтез систем управления космическим кораблем. В настоящее время она решается эмпирическими методами, а не при помощи формализованных математических инструментов. Как правило, разработка систем управления космическими аппаратами представляет собой сложный процесс, включающий сотрудничество большого числа экспертов и ведомств, каждое из которых имеет свои собственные цели и ограничения. Тем не менее можно математически моделировать некоторые подзадачи и получать некоторые качественные результаты расчетов и тенденций, которые могут предоставлять интерес для специалистов. Данная ситуация, когда математические модели являются строгими, но очень сложными для анализа, промежуточная, поэтому лучшее решение – это внедрение системы поддержки принятия решений для выбора эффективных вариантов. Однако возникающие оптимизационные проблемы неразрешимы для большинства известных алгоритмов.

Моделирование процесса управления космическим аппаратом производится при помощи цепей Маркова. Проблема выбора эффективного варианта для системы управления космическим аппаратом формулируется как многомерная задача оптимизации с алгоритмически заданными функциями. В данной работе для решения сложных задач оптимизации будет применяться самоконфигурируемый генетический алгоритм.

Постановка задачи

Система контроля и управления орбитальной группировки спутников связи представляет собой автоматизированную распределенную информационно-управляющую систему, которая включает в свой состав бортовой комплекс управления (БКУ) космическими аппаратами, систему телекоммуникации (СТК), командно-измерительные системы (КИС), а также центр управления полетом (ЦУП). Последние три подсистемы объединены в наземный комплекс управления (НКУ). НКУ взаимодействует с БКУ с помощью СТК, а также КИС и систем передачи данных, которые включают в себя узлы связи, каналы и соответствующее оборудование связи ЦУП. БКУ является подсистемой управления космическим аппаратом, которая в режиме реального времени обеспечивает проверку и контроль состояний бортовых систем, а также выполнение программы полета. Кроме того, БКУ обеспечивает взаимодействие с наземными средствами управления. Контрольные функции, выполняемые системой автоматизированного управления, могут быть разделены на подсистемы, называемые контурами управления, каждый из которых выполняет различные функции. Как правило, можно рассматривать технологический контур, командно-программный, целевой и др. [1].

Модели технологического и командно-про­граммного контуров описаны в таблице 1. В связи с высокой надежностью и стабильностью работы, практической невозможностью двух одновременных отказов, отсутствием последействия для моделирования работы системы управления космическим кораблем могут быть использованы цепи Маркова (рис. 1).

При предварительном проектировании системы управления основной задачей является поиск оптимальных характеристик потоков l1, l2, m1, m2, m3, m4, а также p0, то есть нахождение оптимального распределения функций контура между БКУ и НКУ. Если они являются характеристиками имеющихся вариантов программно-аппаратного оборудования, то существует проблема эффективного выбора варианта, то есть задачи дискретной оптимизации.

Каждый контур имеет свои показатели качества управления, которые не могут быть выражены через показатели качества других контуров. В результате возникает множество проблем при попытке выбрать эффективный вариант системы управления для обеспечения высокого качества в отношении всех контуров управления. Многокритериальность постановки задачи оптимизации – не единственная проблема. Для большинства из контуров управления критерий не может быть представлен в виде аналитической функции своих переменных, но существует в алгоритмической форме, которая требует большого количества вычислений или запуска имитационной модели для оценки значения критерия.

Чтобы иметь возможность выбрать эффективный вариант такой системы управления, нужно промоделировать работу всех контуров управления, а затем объединить результаты в одной оптимизационной задаче с большим количеством моделей, критериев, ограничений и алгоритмически заданными функциями смешанных переменных. Для решения таких задач оптимизации предлагается использовать эволюционные алгоритмы (ЭА), которые известны как хорошие оптимизаторы, не имеющие трудностей с описанными свойствами оптимизационной задачи, такими как смешанные переменные и алгоритмически заданные функции.

Обобщение моделей

В более сложной постановке задачи оптимизации НКУ состоит из трех групп подсистем (КИС, СТК, ЦУП). Учитывая все подсистемы группы как один объект, получим три подсистемы НКУ. Если они могут выходить из строя, то в граф должны быть добавлены новые состояния и переходы.

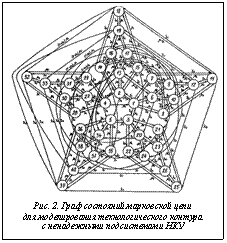
Полный граф состояний для этого случая содержит 40 состояний и 146 переходов (рис. 2). Соответствующая система уравнений Колмогорова содержит 40 строк.

При тех же условиях граф состояний для командно-программного контура содержит 96 состояний и более 300 переходов и не может быть приведен здесь из-за его сложности.

При еще более подробном рассмотрении системы необходимо продолжить деление подсистем группы на части. После этого необходимо объединить все контуры космического корабля и контуры различных космических аппаратов орбитальной группировки. Кроме того, в некоторых случаях невозможно использовать простую цепь Маркова и нужны более сложные имитационные модели. Все это делает задачу выбора эффективного варианта аппаратно-программного комплекса для систем управления космическими аппаратами исключительно сложной для существующих алгоритмов оптимизации.

Применение самоконфигурируемого генетического алгоритма при выборе аппаратно-программного комплекса

Разработанный в [2] самоконфигурируемый генетический алгоритм (SelfCGA), не требующий выбора его настроек, является подходящим методом для решения сложной задачи оптимизации системы управления космическим аппаратом [3]. Прежде всего оценим эффективность его работы на упрощенных моделях технологического и командно-программного контуров с 5 состояниями.

Для выбора эффективного варианта технологического контура необходимо оптимизировать алгоритмически заданную функцию от 6 дискретных переменных. Пространство оптимизации содержит около 1,67×107 вариантов и может быть просмотрено алгоритмом полного перебора в разумные сроки. В такой ситуации известны лучшие и худшие допустимые значения показателей. После выполнения 100 запусков алгоритма известны также лучшие и худшие значения показателей, полученные в результате выполнения.

При численном тестировании использовались 20 индивидов в 30 поколениях. Это означает, что алгоритм просматривает 600 точек из пространства оптимизации, то есть около 0,0036 % от него. В качестве показателя эффективности алгоритма будем использовать надежность (процент запусков алгоритма, которые дали точное решение), MD – максимальное отклонение полученных решений от лучшего известного; и относительное максимальное отклонение полученных решений от лучшего известного RMD. Производилось сравнение пяти групп алгоритмов, а именно четырех групп с различными вариантами модифицированного равномерного скрещивания (UE, UR, UP, UT) и лучшими вариантами других настроек (селекция, мутация) и SelfCGA. В таблице 2 представлены результаты вместе с оценкой вычислительных затрат (усредненное количество поколений, необходимых для нахождения точного решения). Надежностью в условиях данной задачи называется доля прогонов, в которых было достигнуто требуемое качество решения.

Таблица 2

Сравнение надежности алгоритмов для технологического контура с 5 состояниями

Аналогичные оценки для всех трех показателей программно-командного контура даны в таблице 3.

Разница заключается в размере задачи оптимизации. 600 вычислений целевой функции соответствуют 0,057 % от общей размерности пространства оптимизации.

Из таблиц 2 и 3 видно, что SelfCGA превосходит альтернативные алгоритмы для обоих контуров управления и всех показателей. Теперь необходимо оценить эффективность предложенного алгоритма на обобщенных моделях, которые имеют гораздо большие размеры.

Задача поиска оптимального варианта аппаратно-программного комплекса космического аппарата с точки зрения технологического контура управления имеет 11 дискретных переменных. Соответствующее пространство оптимизации содержит около 1,76×1013 точек и не может быть просмотрено при помощи полного перебора, особенно если вспомнить, что рассмотрение одной точки включает решение системы линейных уравнений с 40 переменными. Лучшие и худшие допустимые значения показателей неизвестны, поэтому здесь используются самые лучшие известные решения после нескольких прогонов. Тем не менее можно попытаться получить результирующую таблицу, аналогичную таблице 2.

Таблица 3

Сравнение надежности алгоритмов для командно-программного контура с 5 состояниями

Для оценки производительности алгоритмов мы используем 40 индивидов на одно поколение и 80 поколений за один прогон, то есть алгоритм просматривает около 1,82×10-7 % точек поискового пространства. Результаты численных экспериментов приведены в таблице 4.

Таблица 4

Сравнение надежности алгоритмов для технологического контура с 40 состояниями

Для последней задачи, то есть для модели командно-программного контура управления с 96 состояниями и более 300 переходами, нет подобной информации. Эта задача имеет 13 переменных и содержит 4,5×1015 точек в пространстве оптимизации. Чтобы найти надежные оценки всех показателей, требуется огромное число вычислений. Для нахождения решения алгоритмам требуется просмотреть около 2,2×10-10 % поискового пространства (100 индивидов на 100 поколений). Усредненные результаты 100 прогонов приведены в таблице 5. Это дает нам некоторое представление о сравнительной надежности исследуемого алгоритма.

Таблица 5

Сравнение надежности алгоритмов для командно-программного контура с 96 состояниями

Таблицы 4 и 5 демонстрируют превосходство SelfCGA над всеми альтернативными алгоритмами.

При решении этих задач для реального использования нужно будет сделать только один запуск алгоритма, но с намного большими вычислительными затратами, так как для тестирования намеренно занижались выделяемые вычислительные ресурсы.

В заключение отметим, что при наличии СППР при математическом моделировании систем управления космическими аппаратами, которая позволяет инженеру-проектировщику, не владеющему технологией моделирования с помощью марковских процессов, получать адекватное описание процесса функционирования, основной сложностью при выборе эффективного варианта системы управления космическими аппаратами является оптимизация. Для выбора эффективных вариантов предлагается использовать самоконфигурируемый генетический алгоритм, так как это очень надежный метод, который может эффективно применяться инженерами-проектировщиками космических аппаратов, не имеющими специальных знаний в области эволюционной оптимизации.

Литература

1.     Семенкин Е.С., Семенкина О.Э., Коробейников С.П. Поисковые методы синтеза систем управления  космическими аппаратами. Красноярск: СИБУП, 1996. 325 с.

2.     Семенкина М.Е. Самоадаптивные эволюционные алгоритмы проектирования информационных технологий интеллектуального анализа данных // Искусственный интеллект и принятие решений. 2013. № 1. С. 13–23.

3.     Semenkin E.S., Semenkina M.E. The choice of spacecrafts' control systems effective variants with self-configuring genetic algorithm. Informatics in Control, Automation and Robotics. Proc. 9th Intern. Conf. ICINCO’2012, Rome, Italy, 2012, vol. 1, pp. 84–93.

References

1.     Semenkin E.S., Semenkina O.E., Korobeynikov S.P. Search methods for the synthesis of spacecraft control systems. Krasnoyarsk, Siberian inst. of business, management and psycho­logy Publ., 1996, 325 p.

2.     Semenkina M.E. Self-adaptive evolutionary algorithms for data mining information technologies design. Iskusstvenny intellekt i prinyatiye resheniy [Artificial intelligence and decision making]. 2013, no. 1, pp. 13–23.

3.     Semenkin E.S., Semenkina M.E. The Choice of Space­crafts' Control Systems Effective Variants with Self-Configuring Genetic Algorithm. Informatics in control, automation and robo­tics: proc. of the 9th int. conf. ICINCO’2012. Rome, Italy, 2012, vol. 1, pp. 84–93.