С развитием информационных технологий большое внимание уделяется автоматизированным способам анализа и обработки информации. Создание программного комплекса для автоматизированного учета и прогнозирования состояний больных описывалось в [1]. Одним из важных модулей разработанного программного комплекса является модуль анализа и обработки данных о состоянии здоровья пациента на основе результатов анализов. В данной статье представлены два связанных способа обработки данных: многофакторный анализ данных с использованием метода главных компонент (МГК) [2] и нейронные сети [3, 4]. С по- мощью этих математических методов обрабаты- ваются данные анализов пациента и на их основе прогнозируется правильность лечения с использованием выбранного целевого параметра во времени. На основе значений целевого параметра лечащий врач принимает решения о дальнейших назначениях и путях лечения пациента.
В ходе использования и развития программного комплекса выявлено, что входящими данными для анализа и обработки являются 16 параметров (данные анализов пациентов). В данной статье входящие параметры обозначим X1–X16. Результат обработки информации – предсказанное значение целевого параметра, изменяемое во времени. Задачей модуля программного комплекса является прогнозирование изменения значений целевого параметра во времени исходя из значений входящих параметров X1–X16.
Методы анализа и обработки данных
Многофакторный анализ данных с использованием МГК. МГК дает возможность от непосредственно измеряемых факторов xi (i=1, ..., k) перейти к их некоррелированным линейным комбинациям  (i, j=1, ..., k), которые называют принципиальными компонентами и дисперсии которых убывают, то есть
(i, j=1, ..., k), которые называют принципиальными компонентами и дисперсии которых убывают, то есть  .
.
Коэффициентами линейных комбинаций uij, которые называют нагрузками i-й переменной в j-й компоненте, являются элементы собственных векторов матрицы ковариаций. Дисперсии компонент будут равны собственным числам матрицы ковариаций [2].
Геометрически нахождение главных компонент сводится к переходу к новой ортогональной системе координат. Первую координатную ось определяют так, чтобы соответствующая ей линейная комбинация извлекла возможно большую дисперсию. Вторую ось строят ортогонально первой таким образом, чтобы извлечь наибольшую часть от оставшейся дисперсии. Все оставшиеся компо- ненты определяют аналогично. Таким образом, все компоненты ортогональны друг другу.
От новых координат всегда можно перейти к начальным: 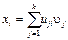 (i, j=1, ..., k), где uj – j-я главная компонента; uij – масса j-й компоненты в i-й переменной.
(i, j=1, ..., k), где uj – j-я главная компонента; uij – масса j-й компоненты в i-й переменной.
Доля дисперсии, выраженная в процентах, объясняемая j-й компонентой, определяется следующим образом: 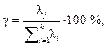 где lj – собственные значения дисперсионно-ковариационной матрицы.
где lj – собственные значения дисперсионно-ковариационной матрицы.
В ряде задач МГК дает возможность значительно снизить размерность задачи за счет того, что линейные комбинации (компоненты), имеющие маленькие дисперсии, отбрасываются, а анализируются лишь линейные комбинации с большими дисперсиями [2], обычно не менее 80 % от общей дисперсии.
Данные, полученные в результате экспериментальных исследований, были обработаны с использованием МГК [5, 6].
 На рисунке 1 представлена диаграмма, отражающая статистические параметры обрабатываемых данных. Из диаграммы видно, что данные сильно различаются по шкалам и требуется их дополнительная обработка.
На рисунке 1 представлена диаграмма, отражающая статистические параметры обрабатываемых данных. Из диаграммы видно, что данные сильно различаются по шкалам и требуется их дополнительная обработка.
Перед применением МГК данные предварительно центрировались и шкалировались отно- сительно стандартного отклонения. Нахождение компонент проводили с использованием самостоятельно разработанного программного пакета. Статистические параметры данных после их обработки показаны на рисунке 2.
 Для оценки того, сколько компонент необходимо для описания данных с заданной точностью (не менее 90 % дисперсии), а сколько можно отбросить и не учитывать в дальнейшем, была построена диаграмма Парето, приведенная на рисунке 3. Из диаграммы видно, что для описания 90 % дисперсии достаточно учесть первые 10 компонент [3]. Рассмотрим их подробнее.
Для оценки того, сколько компонент необходимо для описания данных с заданной точностью (не менее 90 % дисперсии), а сколько можно отбросить и не учитывать в дальнейшем, была построена диаграмма Парето, приведенная на рисунке 3. Из диаграммы видно, что для описания 90 % дисперсии достаточно учесть первые 10 компонент [3]. Рассмотрим их подробнее.
Для визуального представления расположения данных в проекционном пространстве были построены графики счетов для первых десяти компонент (примеры для первых четырех компонент приведены на рисунке 4).
Графики счетов, а также значения коэффициентов перехода к системе координат на основе главных компонент позволяют наглядно представить, как распределены данные, что особенно важно при формировании обучающей и тестовой выборок с помощью различных математических моделей.

 На графике счетов для первых двух компонент (компоненты 1 и 2 на рис. 4) отсутствует явное разделение данных на группы. На графике счетов для вторых двух компонент (компоненты 3 и 4, рис. 4) данные образуют две большие группы, причем данные в них распределены практически равномерно.
На графике счетов для первых двух компонент (компоненты 1 и 2 на рис. 4) отсутствует явное разделение данных на группы. На графике счетов для вторых двух компонент (компоненты 3 и 4, рис. 4) данные образуют две большие группы, причем данные в них распределены практически равномерно.
Из приведенного анализа данных следует отметить, что, формируя обучающие и тестовые выборки, при разработке математического описания необходимо учитывать не только факторы, ко- торые варьировались в ходе проведения экспе- римента, но и ряд характеристик полученных образцов. Обучающая и тестовая выборки должны содержать данные, отличающиеся по этим показателям.
Многофакторный анализ данных позволил заключить, что наибольшее влияние на изменение свойств исследуемого объекта оказывают следующие условия (приводятся в порядке убывания значимости): X2, X3, X5, X4, X6, X1.


 Наглядное представление о связи переменных между собой и их взаимном влиянии дают графики нагрузок – векторные графики в виде двухмерных или трехмерных проекций, приведенные на рисунках 5 и 6. Данные графики читаются следующим образом: чем ближе векторы расположены относительно друг друга, тем большая положительная корреляция имеется между данными; если векторы направлены в диаметрально противоположные стороны, между данными существует сильная обратная корреляция.
Наглядное представление о связи переменных между собой и их взаимном влиянии дают графики нагрузок – векторные графики в виде двухмерных или трехмерных проекций, приведенные на рисунках 5 и 6. Данные графики читаются следующим образом: чем ближе векторы расположены относительно друг друга, тем большая положительная корреляция имеется между данными; если векторы направлены в диаметрально противоположные стороны, между данными существует сильная обратная корреляция.
Из анализа графиков нагрузок можно заметить следующее.
На рисунке 6а показатели морфофункционального статуса эритроцитов попарно коррелированы между собой (пары X13–X16 и X14 –X15) и имеют обратную зависимость: увеличение значений показателей X13 и X16 будет сопровождаться снижением значений показателей X14 и X15. Причем более низкие X3 будут способствовать увеличению показателей, входящих в первую пару.
На рисунке 6б между собой положительно коррелированы такие показатели, как X8 и X9. Между этими двумя показателями и X11 имеется сильная обратная корреляция.
На рисунке 6в более высокий X3, более высокий X6 и больший X7 приводят к увеличению X11 и к большему X14.
На рисунке 6г наблюдается корреляция между X2 и X11: при меньшем X2 меньший X11.
На основе многофакторного анализа было принято, что в качестве входных факторов при построении нейросетевой модели должны быть взяты X2, X3, X5, X6 в связи с отсутствием явной корреляции между ними. Остальные параметры сильно коррелированы между собой и зачастую могут быть выражены функционально относительно друг друга.
Таким образом, использованный метод многофакторного анализа (МГК) позволил сократить размерность задачи, выявил требования к формированию обучающей и тестовой выборок для построения математической модели на основе нейронной сети, а также позволил определить ключевые факторы, которые должны быть использованы в качестве входных параметров в нейросетевой модели.
Использование нейронных сетей. Методы искусственного интеллекта – это современное направление развития методов математического моделирования свойств объектов, динамических процессов и поведения систем. Одним из широ- ко применяемых методов являются нейронные се- ти [7, 8].
Многообразие существующих архитектур нейронных сетей позволяет использовать методы нейроинформатики для решения практически любых классов задач. Чаще всего среди этих задач фигурируют аппроксимация данных, прогнозирование временных рядов, математическое моделирование свойств объектов, распознавание образов, классификация, кластеризация данных, управление.
Искусственные нейронные сети – достаточно сложный математический аппарат. Для их использования зачастую требуются большие объемы исходной информации и значительные вычислительные ресурсы. Поэтому для решения достаточно простых задач целесообразно использовать другие известные и широко применяемые методы. Определим основные понятия нейронных сетей. Искусственный нейрон – это элементарная структурная единица искусственной нейронной сети, выполняющая функции по обработке входных сигналов xi, поступающих с других нейронов, и представлению результата в форме выходного значения.

 Для решения задачи прогнозирования изменения значений целевого параметра во времени были спроектированы и протестированы нейронные сети. Структура нейронной сети, наиболее подходящей для решения задачи [9], представлена на рисунке 7.
Для решения задачи прогнозирования изменения значений целевого параметра во времени были спроектированы и протестированы нейронные сети. Структура нейронной сети, наиболее подходящей для решения задачи [9], представлена на рисунке 7.
Предложенная нейронная сеть была обучена на обучающих выборках (из 200 экспериментов) и проверена с помощью тестовых выборок (из 50 экспериментов). Выходным показателем для нейронной сети был выбранный целевой параметр [10, 11]. На рисунке 8 показано сравнение расчетных и экспериментальных данных во времени.
Ошибка предсказания значения целевого параметра не превышала 8 %. Это дает возможность использовать обученную нейронную сеть для предсказания значений целевого параметра во времени при различных значениях показателей X1–X16.
Расчет по нейронным сетям проводился с помощью созданного ПО, скриншоты которого представлены на рисунке 9.
ПО было реализовано на языке программирования C#. Для его разработки и отладки использовалась среда разработки Visual Studio. Разработанное ПО может быть исполнено на обычном рабочем компьютере и позволяет обработать массив данных до 500 экспериментов за 10 минут.
В заключение отметим, что в статье была проиллюстрирована возможность применения двух современных математических подходов к анализу и обработке данных: многофакторного анализа данных с использованием МГК и нейронных сетей. Данные методы хорошо показали себя при обработке большого массива разнородных данных и выявлении корреляций между данными. Для применения этих методов было разработано ПО, которое позволило обработать исходные данные (анализы пациентов) и на их основе предсказать значение целевого показателя.
Литература
1. Иванов С.И., Тарутина Н.В., Голубчиков М.А., Сафа- ров Р.Р. Программное обеспечение для учета и хранения клинической и социодемографической информации о больных // Программные продукты и системы. 2015. № 3 (111). С. 220–225.
2. Кацюба О.А., Гущин А.В. Численные методы определения оценок параметров многомерного линейного разностного уравнения // Математические методы в технике и технологиях: XVIII Междунар. науч. конф. Казань: Изд-во Казанского гос. технологич. ун-та, 2005. С. 156–159.
3. Cohen M., Elder S., Musco C., Musco C., Persu M. Dimensionality reduction for k-means clustering and low rank approximation (Appendix B), 2014; URL: http://arxiv.org/abs/1410.6801 (дата обращения: 22.12.2015).
4. Gorban A.N., Kegl B., Wunsch D.C., Zinovyev A. (Eds.), Principal Manifolds for Data Visualisation and Dimension Reduction, LNCSE 58, Springer, Berlin – Heidelberg – NY, 2007.
5. Pagès J. Multiple Factor Analysis by Example Using R. CRC Press, 2014, 272 p.
6. Bengio Y., Courville A., Vincent P. Representation Learning: A Review and New Perspectives. Pattern Analysis and Machine Intelligence, 2013, vol. 35, no. 8; URL: http://www.cl.uni-heidelberg.de/courses/ws14/deepl/BengioETAL12.pdf (дата обращения: 22.12.2015).
7. Caudill M. Neural Networks Primer, San Francisco, CA: Miller Freeman Publications, 1987, vol. 2, iss. 12, pp. 46–52.
8. Галушкин А.И. Нейронные сети. Основы теории. М.: Горячая линия–Телеком, 2010. 496 c.
9. Тарков М.С. Нейрокомпьютерные системы. М.: Интернет-Ун-т Информ. Технологий: Бином. Лаборатория знаний, 2006. 142 с.
10. Рутковская Д., Пилиньский М., Рутковский Л. Нейронные сети, генетические алгоритмы и нечеткие системы. М.: Горячая линия–Телеком, 2006. 452 с.
11. Уоссермен Ф. Нейрокомпьютерная техника: теория и практика. М.: Мир, 1992. 184 с.
 (i, j=1, ..., k), которые называют принципиальными компонентами и дисперсии которых убывают, то есть
(i, j=1, ..., k), которые называют принципиальными компонентами и дисперсии которых убывают, то есть  .
.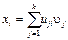 (i, j=1, ..., k), где uj – j-я главная компонента; uij – масса j-й компоненты в i-й переменной.
(i, j=1, ..., k), где uj – j-я главная компонента; uij – масса j-й компоненты в i-й переменной.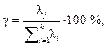 где lj – собственные значения дисперсионно-ковариационной матрицы.
где lj – собственные значения дисперсионно-ковариационной матрицы.








